Di Serokell, kami tidak hanya terlibat dalam proyek komersial, tetapi juga berusaha untuk mengubah dunia menjadi lebih baik. Sebagai contoh, kami sedang berupaya meningkatkan alat utama semua Haskelists - Glasgow Haskell Compiler (GHC). Kami fokus pada perluasan sistem tipe di bawah pengaruh karya Richard Eisenberg, "Tipe Ketergantungan di Haskell: Teori dan Praktek . "

Di blog kami, Vladislav sudah berbicara tentang mengapa Haskell tidak memiliki tipe dependen dan bagaimana kami berencana untuk menambahkannya. Kami memutuskan untuk menerjemahkan pos ini ke dalam bahasa Rusia sehingga sebanyak mungkin pengembang dapat menggunakan tipe dependen dan memberikan kontribusi lebih lanjut pada pengembangan Haskell sebagai bahasa.

Keadaan saat ini

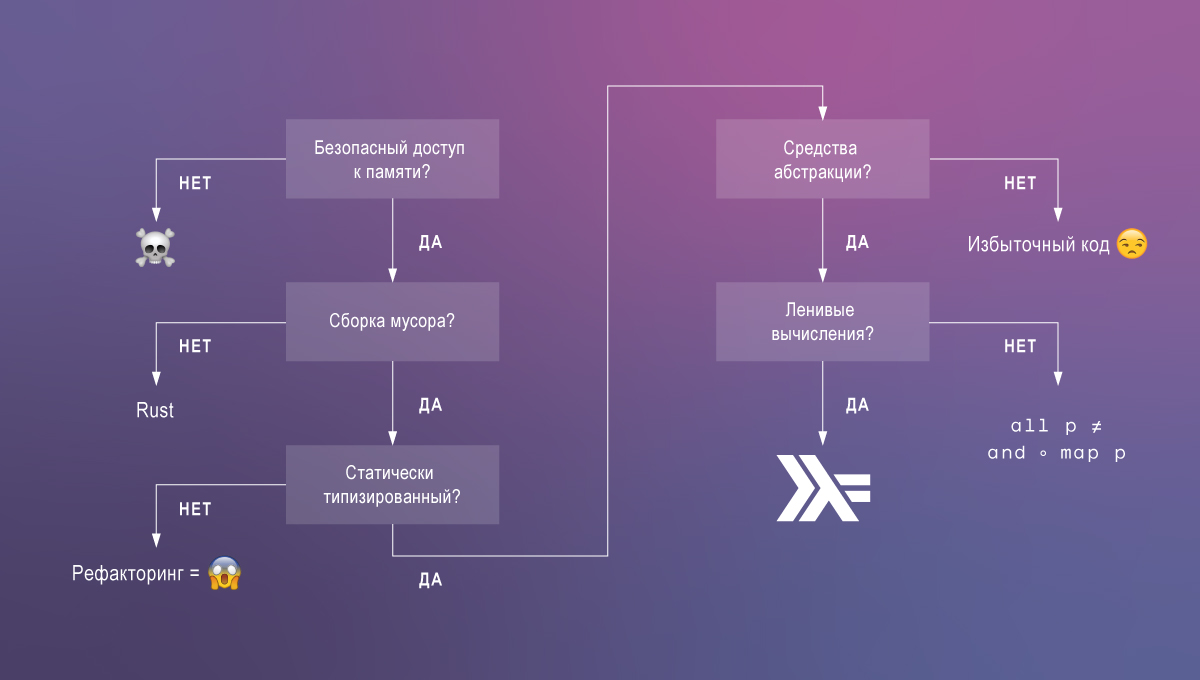
Tipe dependen adalah yang paling saya rindukan di Haskell. Mari kita bahas mengapa. Dari kode yang kita inginkan:

• kinerja, yaitu, kecepatan eksekusi dan konsumsi memori yang rendah;
• pemeliharaan dan kemudahan pemahaman;
• kebenaran dijamin dengan metode kompilasi itu.

Dengan teknologi yang ada, jarang mungkin untuk mencapai ketiga karakteristik, tetapi dengan dukungan untuk tipe-tipe yang bergantung pada Haskell, tugas ini disederhanakan.

Haskell Standard: Ergonomi + Kinerja

Haskell didasarkan pada sistem sederhana: kalkulus lambda polimorfik dengan perhitungan malas, tipe data aljabar, dan kelas tipe. Kombinasi fitur bahasa inilah yang memungkinkan kita untuk menulis kode yang elegan, didukung, dan produktif. Untuk memperkuat klaim ini, kami membandingkan Haskell dengan bahasa yang lebih populer.

Bahasa dengan akses memori yang tidak aman, seperti C, menyebabkan kesalahan dan kerentanan paling serius (misalnya, buffer overflows, kebocoran memori). Kadang-kadang bahasa seperti itu dibutuhkan, tetapi paling sering penggunaannya adalah ide begitu-begitu.

Bahasa akses memori yang aman membentuk dua kelompok: mereka yang mengandalkan pengumpul sampah, dan Rust. Karat tampaknya unik dalam menawarkan akses aman ke memori tanpa pengumpulan sampah . Juga tidak ada lagi Siklon yang didukung dan bahasa riset lainnya dalam grup ini. Tapi tidak seperti mereka, Rust sedang menuju popularitas. Kerugiannya adalah bahwa meskipun ada keamanan, manajemen memori Rust bersifat non-sepele dan manual. Dalam aplikasi yang mampu menggunakan pengumpul sampah, lebih baik menghabiskan waktu pengembang untuk tugas-tugas lain.

Ada bahasa yang tersisa dengan pemulung, yang selanjutnya akan kami bagi menjadi dua kategori berdasarkan sistem tipenya.

Bahasa yang diketik secara dinamis (atau lebih monotip ), seperti JavaScript atau Clojure, tidak memberikan analisis statis, dan karena itu tidak dapat memberikan tingkat kepercayaan yang sama dalam kebenaran kode (dan tidak, tes tidak dapat menggantikan jenis - Anda perlu keduanya) !).

Bahasa yang diketik secara statis seperti Java atau Go seringkali memiliki sistem tipe yang sangat terbatas. Ini memaksa pemrogram untuk menulis kode yang berlebihan dan menempatkan fitur bahasa yang tidak aman. Misalnya, kurangnya tipe generik di Go memaksa penggunaan antarmuka {} dan casting tipe runtime . Juga tidak ada pemisahan antara perhitungan dengan efek samping (input, output) dan perhitungan murni.

Akhirnya, di antara bahasa-bahasa dengan akses memori aman, pengumpul sampah, dan sistem tipe yang kuat, Haskell menonjol karena malas. Komputasi malas sangat berguna untuk menulis kode modular yang dapat disusun. Mereka memungkinkan untuk terdekomposisi menjadi definisi tambahan setiap bagian dari ekspresi, termasuk konstruksi yang mendefinisikan aliran kontrol.

Haskell tampaknya seperti bahasa yang hampir sempurna sampai Anda menyadari seberapa jauh dari mengeluarkan potensi penuh dalam hal verifikasi statis dibandingkan dengan alat bukti teorema seperti Agda .

Sebagai contoh sederhana di mana sistem tipe Haskell tidak cukup kuat, pertimbangkan operator pengindeksan daftar dari Prelude (atau pengindeksan array dari paket primitive ):

 (!!) :: [a] -> Int -> a indexArray :: Array a -> Int -> a 

Tidak ada dalam tanda tangan jenis ini yang mencerminkan persyaratan bahwa indeks harus non-negatif dan kurang dari panjang koleksi. Untuk perangkat lunak dengan persyaratan keandalan tinggi ini tidak dapat diterima.

Agda: ergonomi + kebenaran

Sarana pembuktian teorema (misalnya, Coq ) adalah alat perangkat lunak yang memungkinkan menggunakan komputer untuk mengembangkan bukti formal teorema matematika. Bagi seorang ahli matematika, menggunakan alat seperti itu seperti menulis bukti di atas kertas. Perbedaan dalam kekakuan yang belum pernah terjadi sebelumnya diperlukan oleh komputer untuk menetapkan validitas bukti tersebut.

Untuk programmer, bagaimanapun, cara membuktikan teorema tidak begitu berbeda dari kompiler untuk bahasa pemrograman esoterik dengan sistem tipe yang luar biasa (dan mungkin lingkungan pengembangan terintegrasi), dan biasa-biasa saja (atau bahkan tidak ada) segalanya. Sarana pembuktian teorema adalah, pada kenyataannya, bahasa pemrograman, yang penulis menghabiskan seluruh waktunya mengembangkan sistem pengetikan dan lupa bahwa program masih perlu dijalankan.

Impian yang dihargai dari pengembang perangkat lunak yang diverifikasi adalah cara untuk membuktikan teorema, yang akan menjadi bahasa pemrograman yang baik dengan generator kode berkualitas tinggi dan runtime. Dalam arah ini, termasuk pencipta Idris bereksperimen. Tetapi ini adalah bahasa dengan perhitungan yang ketat (energetik), dan implementasinya saat ini tidak stabil.

Di antara semua cara untuk membuktikan teorema, kaum Haskel dari Agda paling menyukai mereka. Dalam banyak hal, ini mirip dengan Haskell, tetapi dengan sistem tipe yang lebih kuat. Kami di Serokell menggunakannya untuk membuktikan berbagai properti dari program kami. Kolega saya Dania Rogozin menulis serangkaian artikel tentang ini.

Ini adalah tipe fungsi pencarian yang mirip dengan operator Haskell (!!) :

 lookup : ∀ (xs : List A) → Fin (length xs) → A 

Parameter pertama di sini adalah tipe List A , yang sesuai dengan [a] di Haskell. Namun, kami memberinya nama xs untuk merujuknya untuk sisa dari tipe tanda tangan. Di Haskell, kita dapat mengakses argumen fungsi hanya di tubuh fungsi di level istilah:

 (!!) :: [a] -> Int -> a --   xs  (!!) = \xs i -> ... --   xs  

Tapi di Agda, kita bisa merujuk ke nilai xs ini di tingkat tipe, yang kita lakukan di parameter lookup kedua, Fin (length xs) . Fungsi yang merujuk ke parameternya pada level tipe disebut fungsi dependen dan merupakan contoh tipe dependen.

Parameter kedua dalam lookup adalah tipe Fin n untuk n ~ length xs . Nilai tipe Fin n sesuai dengan angka dalam rentang [0, n) , jadi Fin (length xs) adalah angka non-negatif kurang dari panjang daftar input. Inilah yang kami butuhkan untuk menyajikan indeks yang valid dari suatu item daftar. Secara kasar, lookup ["x","y","z"] 2 akan lulus pemeriksaan tipe, tetapi lookup ["x","y","z"] 42 akan gagal.

Ketika menjalankan program Agda, kita dapat mengkompilasinya di Haskell menggunakan backend MAlonzo. Tetapi kinerja dari kode yang dihasilkan tidak memuaskan. Ini bukan kesalahan MAlonzo: dia harus memasukkan banyak unsafeCoerce sehingga GHC unsafeCoerce kode yang sudah diverifikasi oleh Agda. Tetapi unsafeCoerce sama mengurangi kinerja (setelah pembahasan artikel ini, ternyata masalah kinerja mungkin disebabkan oleh alasan lain - catatan penulis) .

Ini menempatkan kami pada posisi yang sulit: kami harus menggunakan Agda untuk pemodelan dan verifikasi formal, dan kemudian menerapkan kembali fungsi yang sama pada Haskell. Dengan organisasi alur kerja ini, kode Agda kami bertindak sebagai spesifikasi yang diverifikasi komputer. Ini lebih baik daripada spesifikasi dalam bahasa alami, tetapi jauh dari ideal. Tujuannya adalah jika kode tersebut dikompilasi, maka ia akan bekerja sesuai dengan spesifikasi.

Haskell dengan Extensions: Correctness + Performance

Bertujuan untuk jaminan statis bahasa dengan tipe dependen, GHC telah datang jauh. Ekstensi ditambahkan padanya untuk meningkatkan ekspresi sistem tipe. Saya mulai menggunakan Haskell ketika GHC 7.4 adalah versi terbaru dari kompiler. Bahkan kemudian, ia memiliki ekstensi utama untuk pemrograman tingkat tipe lanjutan: RankNTypes , GADTs , TypeFamilies , DataKinds , dan PolyKinds .

Namun demikian, masih belum ada tipe dependen lengkap di Haskell: tidak ada fungsi dependen (tipe)) maupun pasangan dependen (tipe Σ). Di sisi lain, setidaknya kita memiliki penyandian untuk mereka!

Praktek saat ini adalah sebagai berikut:

• mengkodekan fungsi level type sebagai keluarga tipe privat,
• menggunakan fungsionalisasi untuk mengaktifkan fungsi tak jenuh,
• menjembatani kesenjangan antara istilah dan tipe menggunakan tipe tunggal.

Ini mengarah ke sejumlah besar kode berlebihan, tetapi perpustakaan singletons mengotomatiskan generasinya melalui Template Haskell.

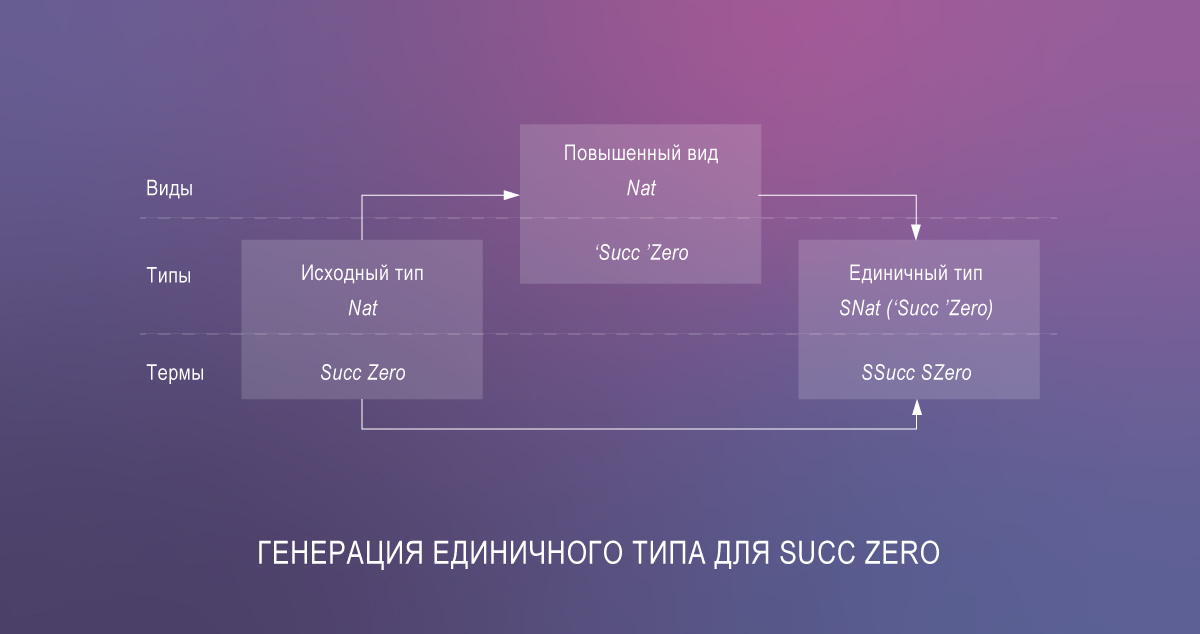
Jadi yang paling berani dan paling menentukan adalah kode jenis-jenis yang bergantung pada Haskell sekarang. Sebagai demonstrasi, berikut ini adalah implementasi dari fungsi lookup mirip dengan varian pada Agda:

 {-# OPTIONS -Wall -Wno-unticked-promoted-constructors -Wno-missing-signatures #-} {-# LANGUAGE LambdaCase, DataKinds, PolyKinds, TypeFamilies, GADTs, ScopedTypeVariables, EmptyCase, UndecidableInstances, TypeSynonymInstances, FlexibleInstances, TypeApplications, TemplateHaskell #-} module ListLookup where import Data.Singletons.TH import Data.Singletons.Prelude singletons [d| data N = Z | SN len :: [a] -> N len [] = Z len (_:xs) = S (len xs) |] data Fin n where FZ :: Fin (S n) FS :: Fin n -> Fin (S n) lookupS :: SingKind a => SList (xs :: [a]) -> Fin (Len xs) -> Demote a lookupS SNil = \case{} lookupS (SCons x xs) = \case FZ -> fromSing x FS i' -> lookupS xs i' 

Dan di sini adalah sesi GHCi yang menunjukkan bahwa pencarian memang menolak indeks yang terlalu besar:

 GHCi, version 8.6.2: http://www.haskell.org/ghc/ :? for help [1 of 1] Compiling ListLookup ( ListLookup.hs, interpreted ) Ok, one module loaded. *ListLookup> :set -XTypeApplications -XDataKinds *ListLookup> lookupS (sing @["x", "y", "z"]) FZ "x" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS FZ) "y" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS (FS FZ)) "z" *ListLookup> lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ))) <interactive>:5:34: error: • Couldn't match type ''S n0' with ''Z' Expected type: Fin (Len '["x", "y", "z"]) Actual type: Fin ('S ('S ('S ('S n0)))) • In the second argument of 'lookupS', namely '(FS (FS (FS FZ)))' In the expression: lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ))) In an equation for 'it': it = lookupS (sing @["x", "y", "z"]) (FS (FS (FS FZ))) 

Contoh ini menunjukkan bahwa kelayakan tidak berarti praktis. Saya senang bahwa Haskell memiliki kemampuan bahasa untuk mengimplementasikan lookupS , tetapi pada saat yang sama saya prihatin dengan kompleksitas yang tidak perlu yang muncul. Di luar proyek penelitian, saya tidak akan merekomendasikan gaya kode seperti itu.

Dalam kasus khusus ini, kita bisa mencapai hasil yang sama dengan kompleksitas yang lebih sedikit menggunakan vektor yang diindeks panjang. Namun, terjemahan kode langsung dari Agda lebih baik mengungkapkan masalah yang harus Anda miliki dalam keadaan lain.

Inilah beberapa di antaranya:

• Relasi pengetikan a :: t dan relasi tujuan dari bentuk t :: k berbeda. 5 :: Integer benar dalam hal, tetapi tidak dalam jenis. "hi" :: Symbol benar dalam tipe, tetapi tidak dalam istilah. Ini mengharuskan Demote tipe Demote untuk memetakan tampilan dan tipe.
• Pustaka standar menggunakan Int sebagai representasi dari indeks daftar (dan singletons menggunakan Nat dalam definisi tinggi). Int dan Nat adalah tipe non-induktif. Meskipun lebih efisien daripada pengkodean bilangan asli, mereka tidak bekerja dengan baik dengan definisi induktif seperti Fin atau lookupS . Karena itu, kami mendefinisikan ulang length sebagai len .
• Haskell tidak memiliki mekanisme bawaan untuk meningkatkan fungsi ke level tipe. singletons mengkode mereka sebagai keluarga tipe pribadi dan menerapkan fungsionalisasi untuk menghindari kurangnya penggunaan sebagian dari keluarga tipe. Pengkodean ini rumit. Selain itu, kami harus memasukkan definisi len dalam kutipan Template Haskell sehingga para singletons menghasilkan mitra tingkat-jenisnya, Len .
• Tidak ada fungsi bawaan bawaan. Kita harus menggunakan tipe unit untuk menjembatani kesenjangan antara istilah dan tipe. Alih-alih daftar yang biasa, kami meneruskan SList ke input pencarian. Karena itu, kita harus mengingat beberapa definisi daftar sekaligus. Ini juga mengarah ke overhead selama eksekusi program. Mereka muncul karena konversi antara nilai biasa dan nilai tipe unit ( toSing , fromSing ) dan karena transfer prosedur konversi (pembatasan SingKind ).

Ketidaknyamanan adalah masalah yang lebih kecil. Lebih buruk lagi, fitur bahasa ini tidak dapat diandalkan. Misalnya, saya melaporkan masalah # 12564 pada tahun 2016, dan ada juga # 12088 di tahun yang sama. Kedua masalah menghambat implementasi program yang lebih maju daripada contoh-contoh dari buku teks (seperti daftar pengindeksan). Bug GHC ini masih belum diperbaiki, dan alasannya, menurut saya, adalah karena pengembang tidak punya cukup waktu. Jumlah orang yang aktif bekerja di GHC ternyata sangat kecil, sehingga beberapa hal tidak dapat diatasi.

Ringkasan

Saya sebutkan sebelumnya bahwa kami ingin ketiga properti dari kode, jadi di sini adalah tabel yang menggambarkan keadaan saat ini:

Masa depan yang cerah

Dari tiga opsi yang tersedia, masing-masing memiliki kekurangan. Namun, kami dapat memperbaikinya:

• Ambil Haskell standar dan tambahkan tipe dependen secara langsung alih-alih pengkodean yang tidak nyaman melalui singletons . (Lebih mudah diucapkan daripada dilakukan.)
• Ambil Agda dan laksanakan penghasil kode efisien dan RTS untuk itu. (Lebih mudah diucapkan daripada dilakukan.)
• Ambil Haskell dengan ekstensi, perbaiki bug, dan terus tambahkan ekstensi baru untuk menyederhanakan pengkodean tipe dependen. (Lebih mudah diucapkan daripada dilakukan.)

Berita baiknya adalah ketiga opsi tersebut bertemu pada satu titik (dalam arti tertentu). Bayangkan ekstensi terkecil dari Haskell standar yang menambahkan tipe dependen, dan karenanya, memungkinkan Anda untuk menjamin kebenaran kode dengan cara itu ditulis. Kode agda dapat dikompilasi (dialihkan) ke bahasa ini tanpa unsafeCoerce . Dan Haskell dengan ekstensi, dalam arti tertentu, merupakan prototipe bahasa ini yang belum selesai. Sesuatu perlu ditingkatkan, dan sesuatu harus dihapus, tetapi pada akhirnya, kita akan mencapai hasil yang diinginkan.

Singkirkan singletons

Indikator kemajuan yang baik adalah penyederhanaan perpustakaan singletons . Karena tipe dependen diterapkan di Haskell, penyelesaian dan penanganan khusus kasus khusus yang diimplementasikan dalam singletons tidak lagi diperlukan. Pada akhirnya, kebutuhan akan paket ini akan hilang sepenuhnya. Misalnya, pada tahun 2016, menggunakan ekstensi -XTypeInType saya menghapus KProxy dari SingKind dan SomeSing . Perubahan ini dimungkinkan melalui penyatuan tipe dan tipe. Bandingkan definisi lama dan baru:

 class (kparam ~ 'KProxy) => SingKind (kparam :: KProxy k) where type DemoteRep kparam :: * fromSing :: SingKind (a :: k) -> DemoteRep kparam toSing :: DemoteRep kparam -> SomeSing kparam type Demote (a :: k) = DemoteRep ('KProxy :: KProxy k) data SomeSing (kproxy :: KProxy k) where SomeSing :: Sing (a :: k) -> SomeSing ('KProxy :: KProxy k) 

Dalam definisi lama, k muncul secara eksklusif di posisi tampilan, di sebelah kanan anotasi bentuk t :: k . Kami menggunakan kparam :: KProxy k untuk mentransfer k ke jenis.

 class SingKind k where type DemoteRep k :: * fromSing :: SingKind (a :: k) -> DemoteRep k toSing :: DemoteRep k -> SomeSing k type Demote (a :: k) = DemoteRep k data SomeSing k where SomeSing :: Sing (a :: k) -> SomeSing k 

Dalam definisi baru, k bergerak bebas antara tampilan dan ketik posisi, jadi kita tidak lagi membutuhkan KProxy . Alasannya adalah bahwa, dimulai dengan GHC 8.0, tipe dan tipe termasuk dalam kategori sintaksis yang sama.

Ada tiga dunia yang sepenuhnya terpisah dalam Haskell standar: istilah, tipe, dan tampilan. Jika Anda melihat kode sumber GHC 7.10, Anda dapat melihat parser terpisah untuk tampilan dan pemeriksaan terpisah. GHC 8.0 tidak lagi memilikinya: parser dan validasi untuk tipe dan tampilan sudah umum.

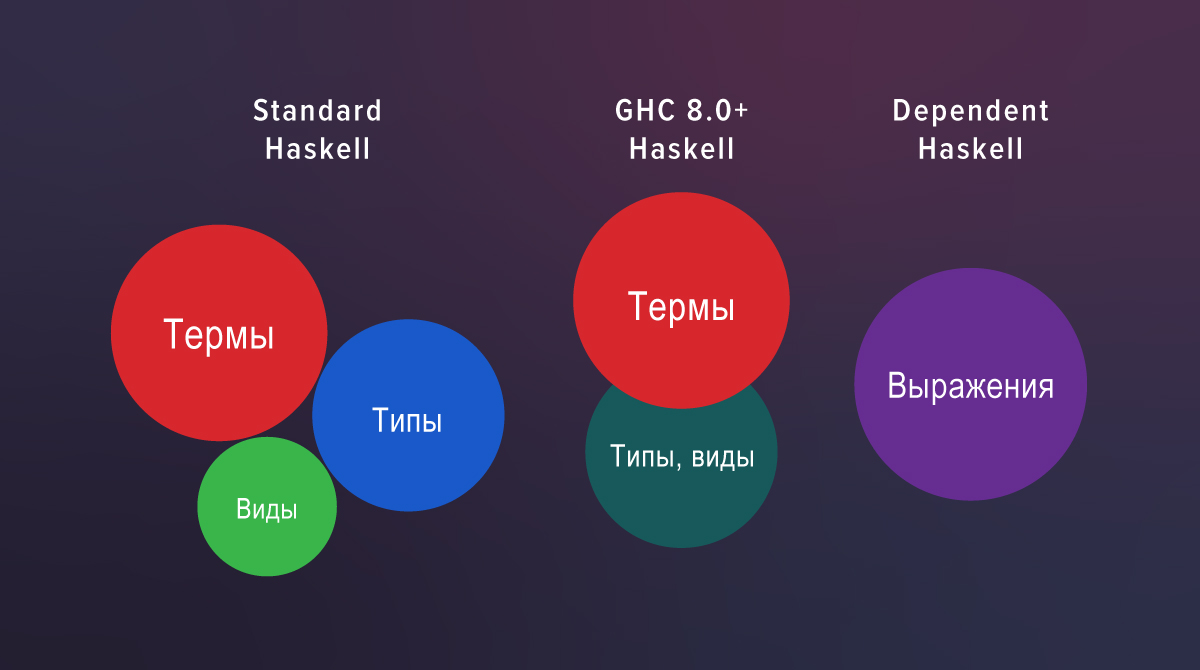
Di Haskell with extensions, view hanyalah peran yang ada di:

 f :: T z -> ... -- 'z'   g :: T (a :: z) -> ... -- 'z'   h :: T z -> T (a :: z) -> ... -- 'z'   ,   

Dalam GHC 8.0-8.4, masih ada beberapa perbedaan antara resolusi nama dalam tipe dan tipe. Tapi saya meminimalkan mereka ke GHC 8.6: Saya membuat ekstensi StarIsType dan memperkenalkan fungsionalitas PolyKinds di PolyKinds . Perbedaan yang tersisa saya buat peringatan untuk GHC 8.8, dan sepenuhnya dihilangkan dalam GHC 8.10

Apa langkah selanjutnya? Mari kita lihat SingKind di versi singletons terbaru:

 class SingKind k where type Demote k = (r :: Type) | r -> k fromSing :: Sing (a :: k) -> Demote k toSing :: Demote k -> SomeSing k 

Keluarga jenis Demote diperlukan untuk menjelaskan perbedaan antara relasi pengetikan a :: t dan relasi tujuan dari form t :: k . Paling sering (untuk tipe data aljabar), Demote adalah pemetaan identitas:

• type Demote Bool = Bool
• type Demote [a] = [Demote a]
• type Demote (Either ab) = Either (Demote a) (Demote b)

Karenanya, Demote (Either [Bool] Bool) = Either [Bool] Bool . Pengamatan ini mendorong kami untuk membuat penyederhanaan berikut:

 class SingKind k where fromSing :: Sing (a :: k) -> k toSing :: k -> SomeSing k 

Demote tidak diperlukan! Dan, pada kenyataannya, ini akan bekerja dengan Either [Bool] Bool dan tipe data aljabar lainnya. Namun dalam praktiknya, kita berurusan dengan tipe data non-aljabar: Integer, Natural , Char , Text , dan sebagainya. Jika digunakan sebagai spesies, mereka tidak dihuni: 1 :: Natural adalah benar pada tingkat istilah, tetapi tidak pada tingkat jenis. Karena itu, kita berurusan dengan definisi seperti itu:

 type Demote Nat = Natural type Demote Symbol = Text 

Solusi untuk masalah ini adalah membesarkan tipe primitif. Misalnya, Text didefinisikan seperti ini:

 -- | A space efficient, packed, unboxed Unicode text type. data Text = Text {-# UNPACK #-} !Array -- payload (Word16 elements) {-# UNPACK #-} !Int -- offset (units of Word16, not Char) {-# UNPACK #-} !Int -- length (units of Word16, not Char) data Array = Array ByteArray# data Int = I# Int# 

Jika kita menaikkan ByteArray# dan Int# ke level tipe, kita bisa menggunakan Text alih-alih Symbol . Dengan melakukan hal yang sama dengan Natural dan mungkin beberapa tipe lainnya, Anda dapat menyingkirkan Demote , bukan?

Sayangnya tidak. Di atas, saya menutup mata untuk tipe data yang paling penting: fungsi. Mereka juga memiliki contoh Demote khusus:

 type Demote (k1 ~> k2) = Demote k1 -> Demote k2 type a ~> b = TyFun ab -> Type data TyFun :: Type -> Type -> Type 

~> ini adalah tipe yang fungsi level-levelnya dikodekan dalam lajang berdasarkan keluarga tipe privat dan fungsionalisasi .

Pada awalnya, mungkin tampak seperti ide yang baik untuk menggabungkan ~> dan -> , karena keduanya berarti tipe (tipe) dari fungsi tersebut. Masalahnya adalah bahwa -> dalam posisi tipe dan -> dalam posisi tampilan memiliki arti yang berbeda. Pada level term, semua fungsi dari a ke b adalah tipe a -> b . Pada level type, hanya konstruktor dari a ke b yang bertipe a -> b , tetapi mereka bukan sinonim dari tipe dan bukan tipe keluarga. Untuk menyimpulkan tipe, GHC mengasumsikan bahwa f ~ g dan a ~ b mengikuti dari fa ~ gb , yang berlaku untuk konstruktor, tetapi tidak untuk fungsi - itu sebabnya ada batasan.

Oleh karena itu, untuk meningkatkan fungsi ke level tipe, tetapi untuk mempertahankan inferensi tipe, kita harus memindahkan konstruktor ke tipe yang berbeda. Kami menyebutnya a :-> b , karena akan benar bahwa f ~ g dan a ~ b mengikuti dari fa ~ gb . Fungsi lainnya masih berupa tipe a -> b . Misalnya, Just :: a :-> Maybe a , tetapi pada saat yang sama isJust :: Maybe a -> Bool .

Ketika Demote selesai, langkah terakhir adalah menyingkirkan Sing itu sendiri. Untuk melakukan ini, kita memerlukan kuantifier baru, hibrida antara forall dan -> . Mari kita lihat lebih dekat fungsi isJust:

 isJust :: forall a. Maybe a -> Bool isJust = \x -> case x of Nothing -> False Just _ -> True 

Fungsi isJust diparameterisasi dengan tipe a dan kemudian dengan nilai x :: Maybe a . Dua parameter ini memiliki sifat yang berbeda:

• Kesederhanaan Dalam isJust (Just "hello") , kita meneruskan x = Just "hello" secara eksplisit, dan a = String secara implisit dihasilkan oleh kompiler. Di Haskell modern, kita juga dapat memaksa lewat eksplisit dari kedua parameter: isJust @String (Just "hello") .
• Relevansi Nilai yang diteruskan ke input ke isJust dalam kode akan ditransmisikan selama pelaksanaan program: kami melakukan perbandingan dengan sampel menggunakan case untuk memeriksa apakah itu tidak Nothing atau Just . Karena itu, nilainya dianggap relevan. Tetapi tipenya dihapus dan tidak dapat dibandingkan dengan polanya: fungsi menangani Maybe Int , Maybe String , Maybe Bool , dll. Karena itu, dianggap tidak relevan. Properti ini juga disebut parametrik.
• Kecanduan. Secara keseluruhan forall a. t forall a. t , tipe t dapat merujuk ke a , dan oleh karena itu, tergantung pada yang dilalui tertentu Sebagai contoh, isJust @String adalah tipe Maybe String -> Bool , dan isJust @Int adalah tipe Maybe Int -> Bool . Ini berarti forall adalah forall dependen. Perhatikan perbedaan dengan parameter nilai: tidak masalah apakah kita memanggil isJust Nothing atau isJust (Just …) , tipe hasilnya selalu Bool . Oleh karena itu, -> adalah penjumlah independen.

Untuk mengeluarkan Sing , kita membutuhkan quantifier yang eksplisit dan relevan, seperti a -> b , dan pada saat yang sama bergantung, seperti forall (a :: k). t forall (a :: k). t . Nyatakan sebagai foreach (a :: k) -> t . Untuk mengeluarkan SingI , kami juga memperkenalkan quantifier dependen relevan yang relevan, foreach (a :: k). t foreach (a :: k). t . Akibatnya, singletons tidak diperlukan karena kami baru saja menambahkan fungsi dependen ke bahasa.

Sekilas tentang Haskell dengan tipe dependen

Dengan naiknya fungsi ke tingkat tipe dan kuantifikasi foreach , kita dapat menulis ulang lookupS sebagai berikut:

 data N = Z | SN len :: [a] -> N len [] = Z len (_:xs) = S (len xs) data Fin n where FZ :: Fin (S n) FS :: Fin n -> Fin (S n) lookupS :: foreach (xs :: [a]) -> Fin (len xs) -> a lookupS [] = \case{} lookupS (x:xs) = \case FZ -> x FS i' -> lookupS xs i' 

Singkatnya, kodenya tidak, namun singletons cukup pandai menyembunyikan kode mubazir. Namun, kode baru ini jauh lebih sederhana: tidak ada lagi Demote , SingKind , SList , SNil , fromSing , fromSing . Tidak ada penggunaan TemplateHaskell , karena sekarang kita dapat memanggil fungsi len secara langsung alih-alih membuat keluarga tipe Len . Kinerja juga akan lebih baik, karena Anda tidak perlu lagi mengkonversi fromSing .

Kita masih harus mendefinisikan ulang length sebagai len untuk mengembalikan N didefinisikan secara induktif daripada Int . Mungkin masalah ini tidak boleh dipertimbangkan dalam kerangka menambahkan tipe dependen ke Haskell, karena Agda juga menggunakan N didefinisikan secara induktif dalam fungsi lookup .

Dalam beberapa aspek, Haskell dengan tipe dependen bahkan lebih sederhana daripada Haskell standar. Namun, dalam istilah itu, tipe dan tipe digabungkan menjadi satu bahasa yang seragam. Saya dapat dengan mudah membayangkan menulis kode dalam gaya ini dalam proyek komersial untuk secara resmi membuktikan kebenaran komponen kunci aplikasi. Banyak perpustakaan Haskell dapat menyediakan antarmuka yang lebih aman tanpa kerumitan singletons .

Ini tidak akan mudah dicapai. Kami dihadapkan dengan banyak masalah teknik yang mempengaruhi semua komponen GHC: parser, resolusi nama, pengecekan tipe, dan bahkan bahasa Core. Semuanya perlu dimodifikasi, atau bahkan sepenuhnya didesain ulang.

Tesaurus