Menjelang peluncuran kursus Algoritma untuk Pengembang berikutnya, kami mengadakan pelajaran terbuka . Mereka berbicara tentang ide yang terkenal dari pohon segmen, membahas bagaimana membangunnya, memperbaruinya, dan dengan cepat O(log n) menghitung jumlah angka dari setiap segmen dari array yang diberikan. Algoritma ini sangat sederhana dan ekonomis: Anda memerlukan O(n) memori. Untuk memperbaiki materi, mereka memecahkan masalah olimpiade.
Webinar ini dilakukan oleh seorang programmer dan guru yang berpengalaman, serta kepala kursus "Algoritma untuk Pengembang"
Evgeny Volosatov .
Pepatah
Pohon segmen adalah struktur data yang memungkinkan penemuan cepat secara algoritmik dan logaritmik dari jumlah elemen array pada segmen tertentu.
Misalnya, bayangkan Anda perlu menemukan jumlah angka-angka berikut:

Dalam hal ini, kita tidak hanya perlu menghitung jumlah angka dari urutan yang ditentukan (jumlah elemen dari array tertentu), tetapi
secepat mungkin untuk menemukan jumlah dari setiap urutan angka-angka ini . Artinya, kita dapat bertanya beberapa interval (segmen) dan memberikan jawabannya secepat mungkin, berapakah jumlah angka dari interval ini:

Apa artinya cepat? Ini berarti
lebih cepat daripada jika kita menambahkan jumlahnya . Bagaimanapun, mungkin ada jutaan dan miliaran angka ...
Adalah keinginan untuk dengan cepat menemukan jumlah elemen yang berurutan yang menjadi motivasi bagi webinar kami. Selain itu, kita berbicara tidak hanya tentang jumlah, tetapi juga tentang tugas-tugas lain, misalnya, menghitung fungsi asosiatif. Jadi, kita berbicara tentang operasi yang pelaksanaannya tidak bergantung pada urutan perhitungan.
Mari kembali ke baris kita:

Jelas, jika kita ingin menemukan hasilnya dengan cepat, kita perlu menghitung beberapa jumlah di muka. Hal pertama yang terlintas dalam pikiran adalah melipat berpasangan:

Sekarang, jika Anda perlu menemukan jumlah angka, kita dapat melakukannya hampir secara instan. Misalnya, untuk menemukan jumlah segmen yang disebutkan di atas, itu akan cukup untuk menambahkan 13 hingga 9. Semuanya dasar: untuk menemukan
jumlah empat angka, kami
hanya menambahkan
dua .
Kami menyulitkan tugas:
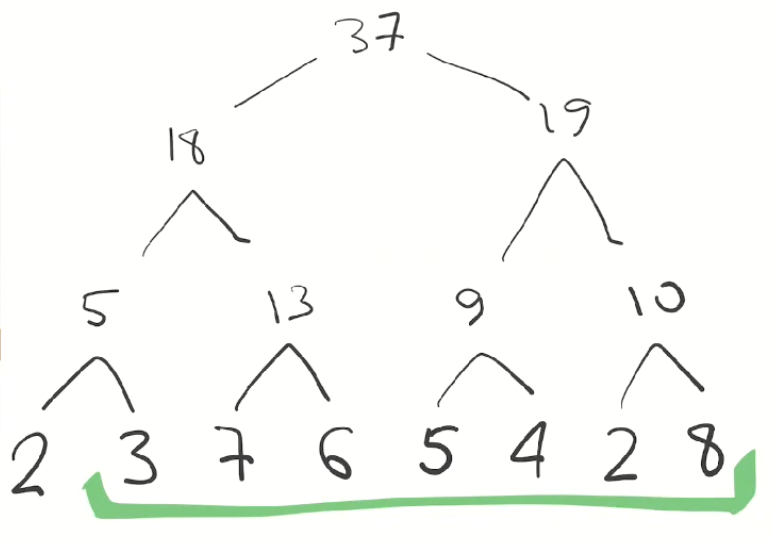
Untuk menemukan jumlah segmen ini, kita perlu menjumlahkan elemen-elemen yang, dengan satu atau lain cara, menutupi segmen kita:

Tentu saja, 3 + 13 + 19 = 35. Perhatikan bahwa untuk menemukan
jumlah dari tujuh angka , kami
hanya menambahkan
tiga . Jika segmen terdiri dari seribu elemen, itu akan cukup untuk menambahkan rata-rata 10 elemen, karena kita memiliki kompleksitas logaritmik dengan logaritma basis-2. Dan itu cepat!
Pohon biner penuh
Pohon biner lengkap adalah pohon, yang masing-masing elemen memiliki tepat dua anak.
Untuk bekerja dengan pohon biner lengkap, Anda bisa dan harus menggunakan struktur data seperti array.
Memberi nomor pada array ini nyaman dari satu . Kami menomori setiap elemen pohon biner dengan bilangan alami dari 1 hingga 2
n -1:

Seluruh keindahan dari pendekatan ini adalah sangat mudah untuk menghitung jumlah anak dan orang tua.
Rumus untuk menghitung "anak kiri":
i * 2 , "kanan":
i * 2 + 1 .

Misalnya, kami menghitung jumlah anak di elemen kelima:
- 5 x 2 = 10 ;
- 5 x 2 + 1 = 11 .
Dan bagaimana dari "anak" untuk naik ke "orang tua"? Kami menggunakan
divisi integer i / 2Oke, dan bagaimana cara menentukan apakah anak itu kiri atau kanan? Jawabannya adalah sebagai berikut:
anak-anak kiri memiliki angka genap, anak-anak kanan memiliki angka ganjil .
Ingat poin-poin ini.
Kembali ke contoh pohon biner kita, kita bertanya pada diri sendiri, bagaimana kita dapat membangunnya? Lihat, pertama-tama kita memiliki array angka:

Untuk itu Anda perlu membangun pohon biner. Berapa banyak memori yang dibutuhkan untuk menyimpan pohon biner, di mana unsur-unsur ini ada di bagian bawahnya?
Jawaban atas pertanyaan ini adalah
2n jika
n adalah kekuatan dua.
Kita melangkah lebih jauh, karena dua pertanyaan muncul sebelum kita:
- dari elemen mana Anda perlu menempatkan nomor sumber dalam array pohon biner lengkap?
- dari elemen mana dan ke arah mana kita akan mulai mengisi pohon kita dengan jumlah yang telah dihitung sebelumnya?

Jawaban untuk pertanyaan pertama cukup sederhana: kita memiliki 8 elemen, secara total akan ada 16 elemen dalam array, yang berarti bahwa elemen pertama akan diberi nomor 16 - 8 = 8. Dan kita akan mulai membangun dari kiri ke kanan dan dari bawah ke atas, mulai dari elemen 7, menambahkan nilai pada anak-anak, seperti ini:

Selanjutnya, Anda perlu menentukan cara menemukan jumlah segmen yang diinginkan. Kami kembali ke contoh pertama kami, menghitung elemen dan mendefinisikan segmen, dan menunjukkan elemen pertama di segmen yang akan ditambahkan oleh huruf L, dan yang terakhir oleh R:

Sekarang perlu untuk memperkenalkan satu konsep lagi sehingga algoritme tindakan jelas. Kita berbicara tentang konsep elemen-elemen fundamental dan segmen-segmen fundamentalnya yang sesuai. Elemen fundamental adalah elemen apa saja dari seluruh array, dan segmen fundamental berhubungan dengannya, yaitu elemen-elemen dari array awal yang merupakan anak / cucu langsungnya. Untuk elemen fundamental dengan nomor 4 "5", segmen fundamental akan dari 8 hingga 9 elemen: ["2"; "3"]:

Sedangkan untuk elemen fundamental dengan angka 10 - "7" (kami menyebutnya L), itu bertepatan dengan segmen fundamentalnya. Apakah mungkin untuk memperluas segmen fundamental ini tanpa melampaui LR? Dalam kasus kami, Anda bisa. Aturan untuk batas kiri adalah ini: jika ia adalah anak kiri, maka segmen fundamental dapat diperluas, elemen fundamental baru akan menjadi induk dari yang sekarang. Yaitu, kita dapat menulis yang berikut dalam program:

Sekarang mari kita beralih ke elemen kanan R. Ini adalah elemen fundamental dan anak kiri, jadi kita tidak bisa lagi memperluas area (kita akan melampaui segmen). Jadi, kita dapat menambahkan elemen ini ke jawabannya:

Selanjutnya, Anda perlu elemen kiri untuk bergerak ke kanan, dan kanan ke kiri. Untuk elemen kiri dengan indeks L = 10, indeks berikutnya adalah 5, karena akan pergi ke induk. Tapi itu akan pergi dulu ke kanan, dan kemudian naik:

Jadi, nilai L pindah ke level yang lebih tinggi dan sedikit ke kanan. Bagaimana R akan berkurang? Menggunakan rumus (R - 1) / 2.

Berikut ini adalah algoritma. Adapun nilai-nilai variabel L dan R berikut, maka mereka akan dipindahkan sebagai berikut:

Jika tidak ada 8 elemen dalam pohon, tetapi angka yang merepotkan, katakanlah 12, kita harus menambahkan pohon (pohon biner harus lengkap) menjadi 16.
Rumus untuk menghitung jumlah elemen (seluruh bagian logaritma diambil):

Sekarang kita menghitung fungsi asosiatif untuk menemukan
minimum . Ini pohon kami dan tebang:

Menurut Anda berapa kali elemen 5 akan terlibat dalam fungsi kita - satu atau dua? Tentu saja, satu, tetapi bagaimana ini diperiksa dalam algoritma? Faktanya, elemen ini adalah putra kiri atau kanan, yang berarti bahwa tindakan akan dilakukan untuk L atau R.
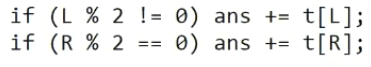
+
Sekarang pertimbangkan operasi perubahan. Katakanlah beberapa elemen telah berubah, misalnya, bukannya 7, 0 masuk. Agar pohon segmen kami tetap dalam kondisi kerja, kita perlu memperbarui semua orangtua, dan kita harus pergi ke bagian paling atas.

Solusi dari masalah olimpiade
Salah satu persyaratan untuk tugas-tugas tersebut adalah semuanya harus bekerja dengan cepat. Jadi, kami memiliki kondisi berikut:

Kami akan menyelesaikannya dengan menggunakan pengetahuan tentang pohon segmen. Hasilnya, kami mendapatkan kode C # berikut:

Kami mengirimkannya untuk verifikasi, kami melihat bahwa
keputusan telah dibuat dan lengkap , yang berarti bahwa algoritma kami berfungsi.

Itu saja, jika Anda ingin detail lebih lanjut,
tonton seluruh video . Anda juga dapat membaca dengan santai artikel penulis berikut oleh guru kami
Evgeny Volosatov di Habré:
-
Menyeimbangkan pohon merah-hitam - Tiga kasus ;
-
Kuda itu bergerak sedikit. Bitboard Catur .