Seluruh geografi: tugas navigasi dan geodetik dalam berbagai bahasa

Salam sayang!

“... tempat kapal yang sebenarnya, meskipun tidak diketahui, tidak disengaja, tetapi, tidak diketahui pada titik mana” V. Aleksishin dkk. Navigasi Praktis, 2006. hlm. 71

"Pejalan kaki keluar dari dua tepi galaksi ..." (C) Sergey Popov (Ahli Astrofisika)

Mengingat tren baru dalam gaya Art Nouveau, saya ingin menulis tentang memecahkan masalah geodetik di tanah datar. Namun sejauh ini, pernyataan bahwa bentuk bumi dengan mudah didekati oleh ellipsoid bukanlah bidaah dan hasutan, saya mengundang semua yang tertarik untuk bergabung dengan model yang lebih konservatif.

• jarak antara dua titik geografis
• penentuan titik dengan diketahui, jarak ke sana dan sudut azimut
• penentuan posisi suatu titik dengan jarak yang diukur ke titik yang diketahui (TOA, TOF)
• penentuan posisi suatu titik dengan waktu kedatangan sinyal yang diukur (TDOA)

Semua ini dalam C #, Rust dan Matlab, pada bola dan ellipsoid, dengan gambar, grafik, kode sumber - di bawah potongan.

Dan ini, KDPV yang relevan:



Bagi mereka yang terburu-buru (saya sendiri), di sini adalah repositori di GitHub , di mana semua kode sumber dengan tes dan contoh ada.

Repositori dikelola dengan sangat sederhana: perpustakaan saat ini disajikan dalam tiga bahasa dan setiap implementasi ada di foldernya sendiri:

• C #
• Karat
• Matlab

Implementasi paling lengkap di C #: tidak seperti yang lain, ada yang disebut metode di dalamnya virtual long base - ini adalah ketika sebuah objek yang posisinya perlu Anda tentukan stasioner, dan ada jarak yang diukur dari berbagai titik, dengan posisi yang diketahui.

Untuk melihat bagaimana semuanya bekerja, dengan parameter apa yang dipanggil dan dikembalikan, dan melakukan pengintaian dalam pertempuran, ada demo dan tes yang berbeda:

• Uji aplikasi konsol dalam C #
• Tes seluruh perpustakaan di Matlab
• Skrip demo TOA / TDOA dengan gambar-gambar indah di Matlab
• Skrip pada Matlab untuk membandingkan keakuratan solusi untuk masalah geodesik pada bola (persamaan Haversine) dan pada ellipsoid (persamaan Vincenty)
• Untuk implementasi pada Rust , kode perpustakaan berisi tes. Dan Anda dapat melihat bagaimana semuanya bekerja hanya dengan menjalankan perintah "Cargo -test"

Saya mencoba membuat perpustakaan sebagai mandiri dan mandiri mungkin. Sehingga jika Anda mau, Anda bisa mengambil bagian yang diinginkan (merujuk ke sumbernya, tentu saja), tanpa menyeret yang lainnya.

Hampir selalu sudut dalam radian, jarak dalam meter, waktu dalam detik.

Sekarang, mari kita mulai dari awal:

Tugas survei

Ada dua tugas geodetik yang khas: langsung dan terbalik.

Jika misalnya, saya tahu koordinat saya saat ini (lintang dan bujur), dan kemudian saya berjalan 1000 kilometer ke timur laut, sumur, atau utara. Koordinat apa yang akan saya miliki sekarang? - Untuk mengetahui koordinat apa yang akan saya miliki adalah untuk menyelesaikan masalah geodesik langsung.

Yaitu: Tugas geodesik langsung adalah menemukan koordinat suatu titik dengan jarak yang diketahui dan sudut arah.

Dengan masalah terbalik, semuanya benar-benar jelas - misalnya, saya menentukan koordinat saya, dan kemudian saya berjalan untuk beberapa waktu dalam garis lurus dan lagi menentukan koordinat saya. Menemukan berapa banyak yang saya lakukan berarti menyelesaikan masalah geodesik terbalik.

Yaitu: Masalah geodesik terbalik adalah menemukan jarak antara dua titik dengan koordinat geografis yang diketahui.

Anda dapat memecahkan masalah ini dalam beberapa cara, tergantung pada keakuratan yang diperlukan dan waktu yang Anda ingin habiskan untuk itu.

Cara termudah adalah membayangkan bahwa bumi itu datar - ini adalah sebuah bola. Ayo kita coba.
Berikut adalah rumus untuk menyelesaikan masalah langsung ( sumber ):

$$

$$\ phi_2 = arcsin (sin \ phi_1cos \ delta + cos \ phi_1sin \ delta cos \ theta)$$

$$

$$\ lambda_2 = \ lambda_1 + atan2 (sin \ theta sin \ delta cos \ phi_1, cos \ delta-sin \ phi_1sin \ phi_2)$$

Di sini $$$\ phi_1$ , $$$\ lambda_1$ - lintang dan bujur dari titik awal, $$$\ theta$ - sudut arah, diukur searah jarum jam dari arah utara (jika dilihat dari atas), $$$\ delta$ - jarak sudut d / R. d adalah jarak yang diukur (ditempuh), dan R adalah jari-jari bumi. $$$\ phi_2$ , $$$\ lambda_2$ - lintang dan bujur dari titik yang diinginkan (yang kita datangi).

Untuk mengatasi masalah terbalik, ada satu lagi (rumus yang tidak kalah sederhana):

$$

$$a = sin ^ 2 (\ Delta \ phi / 2) + cos \ phi_1 cos \ phi_2 sin ^ 2 (\ Delta \ lambda / 2)$$

$$

$$d = R * atan2 (\ sqrt a, \ sqrt {1-a})$$

Dimana $$$\ phi_1$ , $$$\ lambda_1$ dan $$$\ phi_2$ , $$$\ lambda_2$ - Koordinat titik, R - radius bumi.

Rumus yang dijelaskan disebut Persamaan Haversine.

• Dalam implementasi C #, fungsi yang sesuai disebut HaversineDirect dan HaversineInverse dan tinggal di Algorithms.cs .
• Dalam implementasi Karat, ini adalah fungsi haversine_direct dan haversine_inverse .
• Akhirnya, di Matlab, fungsi disimpan dalam file yang terpisah, dan berikut adalah kedua fungsinya:
  HaversineDirect dan HaversineInverse

Untuk C #, saya akan memberikan nama-nama fungsi dan tautan ke file di mana mereka berada. Untuk Rust - hanya nama-nama fungsi (karena seluruh perpustakaan dalam satu file), dan untuk Matlab - tautan ke file skrip yang sesuai, karena di Matlab ada satu fungsi - satu skrip.

Jelas, ada beberapa jenis tangkapan: bumi bukan bola, tetapi pesawat, dan ini entah bagaimana harus memengaruhi penerapan rumus-rumus ini dan / atau keakuratan solusinya.

Dan sungguh. Tetapi untuk menentukan ini, Anda perlu membandingkan dengan sesuatu.
Kembali pada tahun 1975, Thaddeus Vincenty menerbitkan solusi komputasi efisien masalah geodesik langsung dan terbalik pada permukaan spheroid (lebih dikenal sebagai Ellipsoid Revolusi, kawan! Ellisoid of Rotation), yang telah menjadi hampir standar.

Deskripsi perangkat metode ditarik ke artikel terpisah, jadi saya akan membatasi diri hanya untuk mengirim ke karya asli Vincenti dan ke kalkulator online dengan deskripsi algoritme.

Di perpustakaan UCNLNav, solusi masalah geodesik langsung dan terbalik menggunakan rumus Vincenti terletak pada fungsi-fungsi berikut:

• C #: VincentyDirect dan VincentyInverse di Algorithms.cs .
• Karat: vincenty_inverse dan vincenty_direct
• Matlab: Nav_vincenty_direct dan Nav_vincenty_inverse .

Karena Solusi Vincenti adalah iteratif, maka jumlah iterasi maksimum (it_limit) ada di daftar parameter, dan jumlah iterasi yang sebenarnya ada di daftar hasil. Ada juga ambang yang menentukan kondisi berhenti (epsilon). Dalam kebanyakan kasus, tidak lebih dari 10 iterasi diperlukan, tetapi untuk hampir poin antipodal (seperti kutub utara dan selatan) metode ini konvergen buruk, dan hingga 2000 iterasi mungkin diperlukan.

Perbedaan yang paling penting adalah bahwa formula ini mengeksekusi solusi pada spheroid, dan parameternya harus ditransfer ke fungsi. Ada struktur sederhana untuk ini yang menggambarkannya.

Dalam semua implementasi, salah satu ellipsoid standar dapat diperoleh dalam satu baris. (Sangat sering, WGS84 [https://en.wikipedia.org/wiki/World_Geodetic_System] digunakan dan kami akan memberikannya sebagai contoh):

• Dalam C #: Algorithms.cs memiliki bidang statis Algorithms.WGS84Ellipsoid - dapat diteruskan ke metode.
• Pada Karat:

  let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); 

• Di Matlab:

   el = Nav_build_standard_ellipsoid('WGS84'); 

Nama parameter yang tersisa cukup jelas dan tidak boleh menyebabkan ambiguitas.

Untuk memahami berapa biayanya bagi kita untuk menggunakan solusi untuk bola bukannya elips, ada skrip pada implementasi Matlab.

Matlab sangat nyaman untuk menampilkan apa pun tanpa gerakan yang tidak perlu, jadi saya memilihnya untuk demonstrasi.

Logika naskahnya:

1. Kami mengambil titik dengan koordinat sewenang-wenang

 sp_lat_rad = degtorad(48.527683); sp_lon_rad = degtorad(44.558815); 

dan arah yang berubah-ubah (saya memilih sekitar barat):

 fwd_az_rad = 1.5 * pi + (rand * pi / 4 - pi / 8); 

2. Kami melangkah dari itu ke jarak yang semakin meningkat. Mengapa kami segera mengatur jumlah langkah dan ukuran langkah:

 n_samples = 10000; step_m = 1000; % meters distances = (1:n_samples) .* step_m; 

3. Untuk setiap langkah, kami memecahkan masalah geodesik langsung pada bola dan pada ellipsoid, mendapatkan titik yang diinginkan:

 [ h_lats_rad(idx), h_lons_rad(idx) ] = Nav_haversine_direct(sp_lat_rad,... sp_lon_rad,... distances(idx),... fwd_az_rad,... el.mjsa_m); [ v_lats_rad(idx), v_lons_rad(idx), v_rev_az_rad, v_its ] = Nav_vincenty_direct(sp_lat_rad,... sp_lon_rad,... fwd_az_rad,... distances(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

4. Untuk setiap langkah, kami memecahkan masalah geodesik terbalik - kami menghitung jarak antara hasil yang diperoleh pada bola dan ellipsoid:

 [ v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(h_lats_rad(idx),... h_lons_rad(idx),... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); 

5. Kami memeriksa solusi langsung terbalik untuk kedua metode:

 [ ip_v_dist(idx) a_az_rad, a_raz_rad, its, is_ok ] = Nav_vincenty_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el,... VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); ip_h_dist(idx) = Nav_haversine_inverse(sp_lat_rad,... sp_lon_rad,... v_lats_rad(idx),... v_lons_rad(idx),... el.mjsa_m); 

Dalam skrip, urutan ini dilakukan pertama untuk langkah = 1000 m, dan kemudian untuk langkah = 1 meter.

Pertama, mari kita lihat bagaimana hasil keputusan langsung berbeda dalam koordinat (lintang dan bujur), yang kami hitung vektor "delta", karena semuanya ditulis di Matlab dalam satu baris:

 d_lat_deg = radtodeg(v_lats_rad - h_lats_rad); %    ( ) d_lon_deg = radtodeg(v_lons_rad - h_lons_rad); %    ( ) 

Pada sumbu, absis akan ditampilkan pada skala logaritmik, karena jarak kami bervariasi dari 1 hingga 10.000 km:

 figure semilogx(distances, d_lat_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Latitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); figure semilogx(distances, d_lon_deg, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Longitude difference)'); xlabel('Distance, m'); ylabel('Difference, °'); 

Hasilnya, kami mendapatkan grafik untuk lintang seperti itu:



Dan untuk garis bujur:



Saya tidak mengerti dalam derajat, saya selalu dibimbing oleh metode untuk memperkirakan "dengan mata":
1 ° dari sesuatu adalah rata-rata 100-110 km. Dan jika kesalahan lebih dari sepersejuta atau setidaknya seratus ribu bagian derajat - ini adalah berita buruk.

Selanjutnya, kita melihat jarak antara titik awal dan titik yang diperoleh pada setiap langkah sesuai dengan rumus untuk bola dan ellipsoid. Kami menghitung jarak menggunakan rumus Vincenti (karena jelas lebih akurat - penulis menjanjikan kesalahan dalam milimeter). Bagan dalam meter dan kilometer jauh lebih nyata dan akrab:

 figure semilogx(distances, v_dist, 'r'); title('Direct geodetic problem: Vincenty vs. Haversine (Endpoint difference by Vincenty)'); xlabel('Distance, m'); ylabel('Difference, m'); 

Hasilnya, kita mendapatkan gambar berikut:



Ternyata pada rentang 10.000 km metode-metode berbeda 10 km.

Jika sekarang semuanya diulang untuk langkah 1000 kali lebih kecil, mis. ketika seluruh rentang di sepanjang sumbu X tidak 10.000 km tetapi hanya 10 km, gambarnya sebagai berikut:



Yaitu, pada jarak 10 km hanya 20 meter, dan untuk 1-2 meter formula hanya berbeda pada jarak sekitar 1000 meter.

Kesimpulan kapten jelas: jika akurasi formula dengan solusi di bola cukup untuk masalah, maka kami menggunakannya - mereka lebih mudah dan lebih cepat.

Nah, bagi mereka yang akurasi milimeternya tidak cukup, pada 2013 sebuah karya diterbitkan yang menjelaskan solusi masalah geodetik dengan nanometer (!) Akurasi. Saya tidak yakin bahwa saya bisa segera menemukan di mana mungkin diperlukan - kecuali untuk survei geodesi ketika membangun detektor gelombang gravitasi atau sesuatu yang benar-benar fantastis).

Sekarang mari kita beralih ke yang terlezat:

Memecahkan masalah navigasi

Saat ini, perpustakaan dapat menentukan:

• Lokasi objek berdasarkan jarak ke titik, dengan koordinat yang diketahui dalam 2D ​​dan 3D. Inilah yang kami sebut TOA - Waktu Kedatangan (atau lebih tepatnya, TOF - Waktu Penerbangan)
• Lokasi objek berdasarkan perbedaan waktu kedatangan dalam 2D ​​dan 3D. Inilah yang kami sebut TDOA (Perbedaan Waktu Kedatangan).

Pada kenyataannya, kami selalu mengukur rentang atau waktu kedatangan sinyal (dan, sesuai, perbedaannya) dengan kesalahan, dengan noise. Oleh karena itu, solusi masalah navigasi di sebagian besar kasus adalah meminimalkan kesalahan. Metode kuadrat terkecil dan itu saja .

Apa yang perlu diminimalkan disebut fungsi residual.

Untuk tugas-tugas TOA, terlihat seperti ini:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2 )} - r_i] ^ 2$$

Dimana $$$\ epsilon (x, y, z)$ - nilai fungsi residual untuk titik tertentu dengan koordinat $$$(x, y, z)$ ; N adalah jumlah titik kontrol yang memiliki koordinat $$$(x_i, y_i, z_i)$ , $$$r_i$ - Jarak terukur dari titik referensi ke objek yang diposisikan.

Dan untuk tugas TDOA seperti ini:

$$

$$argmin \ epsilon (x, y, z) = \ sum_ {i = 1, j = 2, i \ neq j} ^ {N} [\ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2+ (z-z_i) ^ 2)} - \\ \ sqrt {(x-x_j) ^ 2 + (y-y_j) ^ 2 + (z-z_j) ^ 2)} - \ nu (t_ {Ai} -t_ {Aj})] ^ 2$$

Semuanya sama di sini, hanya pasangan titik referensi dan waktu kedatangan yang sesuai yang dipertimbangkan $$$t_ {Ai}$ dan $$$t_ {Aj}$ , dan $$$\ nu$ - Kecepatan rambat sinyal.

Maka fungsi-fungsi ini terlihat dalam kode:




Seperti yang Anda lihat, kedua fungsi bekerja dengan sejumlah variabel titik kontrol atau garis. Secara umum, tugas dapat berbeda, dan fungsi residual juga.

Misalnya, Anda dapat memecahkan masalah tidak hanya menentukan lokasi, tetapi juga menentukan orientasi. Dalam hal ini, fungsi residual akan mengandung satu atau lebih sudut.

Mari kita membahas lebih dalam tentang struktur internal perpustakaan

Pada tahap ini, perpustakaan bekerja dengan tugas-tugas 2D dan 3D dan pemecahnya sendiri tidak tahu dan tidak ingin tahu seperti apa fungsi yang diminimalkan itu. Ini dicapai dengan cara berikut.

Solver memiliki dua aspek: 2D dan 3D solver berdasarkan metode Nelder-Mead atau, seperti juga disebut, metode Simplex.

Karena metode ini tidak memerlukan perhitungan turunan (yang disebut minimisasi bebas turunan ), idealnya, pengguna perpustakaan dapat menggunakan fungsi residunya sendiri jika perlu. Plus, secara teori tidak ada batas atas pada jumlah titik kontrol yang digunakan dalam menyelesaikan masalah.

Dalam C # dan Rust, 2D dan 3D Solver adalah metode Generik:

 public static void NLM2D_Solve<T>(Func<T[], double, double, double, double> eps, T[] baseElements,... //       : fxi[0] = eps(baseElements, xix[0], xiy[0], z); 

Contoh menyebut pemecah itu sendiri:

 public static void TOA_NLM2D_Solve(TOABasePoint[] basePoints, double xPrev, double yPrev, double z, int maxIterations, double precisionThreshold, double simplexSize, out double xBest, out double yBest, out double radialError, out int itCnt) { NLM2D_Solve<TOABasePoint>(Eps_TOA3D, basePoints, xPrev, yPrev, z, maxIterations, precisionThreshold, simplexSize, out xBest, out yBest, out radialError, out itCnt); } 

Di Rust ...

 pub fn nlm_2d_solve<T>(eps: Eps3dFunc<T>, base_elements: &Vec<T>... 

Semuanya identik, akurat dengan sintaks bahasa.

Di Matlabe, dengan kesukarelaan yang melekat, pemecah sendiri tidak tahu apa elemen dasar yang diteruskan kepadanya - pemakai itu sendiri harus memastikan bahwa tautan ke fungsi residual dan sekumpulan elemen pendukung yang dikirimkan ke pemecah kompatibel:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(eps, base_elements, .... 

Dan karenanya, panggilan ke pemecah terlihat seperti ini:

 function [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size) [ x_best, y_best, rerr, it_cnt ] = Nav_nlm_2d_solve(@Nav_eps_toa3d, base_points, x_prev, y_prev, z,... max_iterations, precision_threshold, simplex_size); end 

Ada skrip Matlab khusus untuk menunjukkan solusi masalah TOA dan TDOA.

Demonstrasi dalam 2D ​​tidak dipilih secara kebetulan - Saya tidak yakin saya bisa mengetahui cara menampilkan fungsi residual tiga dimensi secara sederhana dan informatif =)

Jadi Di awal skrip ada beberapa parameter yang bisa diubah:

 %% parameters n_base_points = 4; %    area_width_m = 1000; %   max_depth_m = 100; %   ( Z) propagation_velocity = 1500;%     -  max_iterations = 2000; %    precision_threshold = 1E-9; %   simplex_size = 1; %      contour_levels = 32; %      range_measurements_error = 0.01; % 0.01 means 1% of corresponding slant range %    -   1% 

Posisi titik yang diinginkan diatur secara acak di area yang ditentukan:

 %% actual target location r_ = rand * area_width_m / 2; az_ = rand * 2 * pi; actual_target_x = r_ * cos(az_); actual_target_y = r_ * sin(az_); actual_target_z = rand * max_depth_m; 

Selanjutnya, tempatkan secara acak titik kontrol, hitung jarak dari yang diinginkan dan tampilkan semuanya:

 %% base points figure hold on grid on base_points = zeros(n_base_points, 4); for n = 1:n_base_points r_ = area_width_m / 2 - rand * area_width_m / 4; az_ = (n - 1) * 2 * pi / n_base_points; base_x = r_ * cos(az_); base_y = r_ * sin(az_); base_z = rand * max_depth_m; dist_to_target = Nav_dist_3d(base_x, base_y, base_z, actual_target_x, actual_target_y, actual_target_z); base_points(n, :) = [ base_x base_y base_z dist_to_target ]; end N =1:n_base_points; plot3(actual_target_x, actual_target_y, actual_target_z,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot3(base_points(N, 1), base_points(N, 2), base_points(N, 3),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); for n = 1:n_base_points line([ actual_target_x, base_points(n, 1) ], [ actual_target_y, base_points(n, 2) ], [ actual_target_z, base_points(n, 3) ]); end view(45, 15); legend('target', 'base points'); title('Placement of base stations and the target'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); zlabel('Z coordinate, m'); 

Hasilnya, kita mendapatkan gambar berikut:



Tambahkan kesalahan acak ke pengukuran jarak:

 % adding range measurement errors base_points(N, 4) = base_points(N, 4) + base_points(N, 4) *... (rand * range_measurements_error - range_measurements_error / 2); 

Kami membangun fungsi residual untuk wilayah yang dipilih dengan penipisan tertentu - jika tidak, perhitungannya dapat memakan waktu lama. Saya memilih ukuran area 1000 x 1000 meter dan saya mempertimbangkan fungsi residual di seluruh area setelah 10 meter:

 % error surface tiles tile_size_m = 10; n_tiles = area_width_m / tile_size_m; %% TOA solution error_surface_toa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_toa(t_x, t_y) = Nav_eps_toa3d(base_points,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf_a = [1:n_tiles] * tile_size_m - area_width_m / 2; surf(surf_a, surf_a, error_surface_toa); title('TOA solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

Berikut adalah fungsi residual:



Tentu saja, saya agak licik - posisi relatif dari titik kontrol dan yang diinginkan dipilih sehingga mereka selalu membentuk sosok cembung dengan titik yang diinginkan di dalam. Sebagian besar karena ini, permukaan memiliki satu minimum, yang tanpa masalah.

Seorang pembaca yang sombong dapat mengubah urutan hal-hal ini dan mencoba untuk mengatur titik jangkar dan yang diinginkan secara tidak sengaja.

Sekarang tampilkan semuanya bersama-sama. Ini sulit dilakukan di permukaan - nilai yang berbeda di sepanjang sumbu vertikal. Oleh karena itu, lebih mudah untuk menggambar semuanya pada irisan dua dimensi:

 figure hold on contourf(surf_a, surf_a, error_surface_toa, contour_levels); plot(actual_target_x, actual_target_y,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(base_points(N, 1), base_points(N, 2),... 'o',... 'MarkerFaceColor', 'green',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); [ x_prev, y_prev ] = Nav_toa_circles_1d_solve(base_points, actual_target_z, pi / 180, 10, 0.1); [ x_best, y_best, rerr, it_cnt ] = Nav_toa_nlm_2d_solve(base_points, x_prev, y_prev, actual_target_z,... max_iterations, precision_threshold, simplex_size); plot(x_best, y_best,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); title(sprintf('TOA Solution: Residual function. Target location estimated with E_{radial} = %.3f m in %d iterations', rerr, it_cnt)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Residual function value', 'Actual target location', 'Base points', 'Estimated target location'); 

Hasilnya kira-kira seperti ini:



Kesalahan radial ditampilkan di header grafik - akar dari nilai akhir dari fungsi residual. Grafik menunjukkan bahwa lokasi sebenarnya dan yang dihitung berada dalam persetujuan yang baik, tetapi skalanya tidak memungkinkan kami untuk menentukan seberapa baik.

Oleh karena itu, kami menampilkan lokasi terhitung dari titik yang diinginkan dan lokasi sebenarnya secara terpisah dan menghitung jarak di antara mereka:

 figure hold on grid on dx = actual_target_x - x_best; dy = actual_target_y - y_best; plot(0, 0,... 'p',... 'MarkerFaceColor', 'red',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 15); plot(dx, dy,... 'd',... 'MarkerFaceColor', 'yellow',... 'MarkerEdgeColor', 'blue',... 'MarkerSize', 7); plot(-dx * 2, -dy * 2, '.w'); plot(dx * 2, dy * 2, '.w'); d_delta = Nav_dist_3d(actual_target_x, actual_target_y, actual_target_z, x_best, y_best, actual_target_z); title(sprintf('TOA Solution: Actual vs. Estimated location, distance: %.3f m', d_delta)); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); legend('Actual target location', 'Estimated target location'); 

Begini tampilannya:



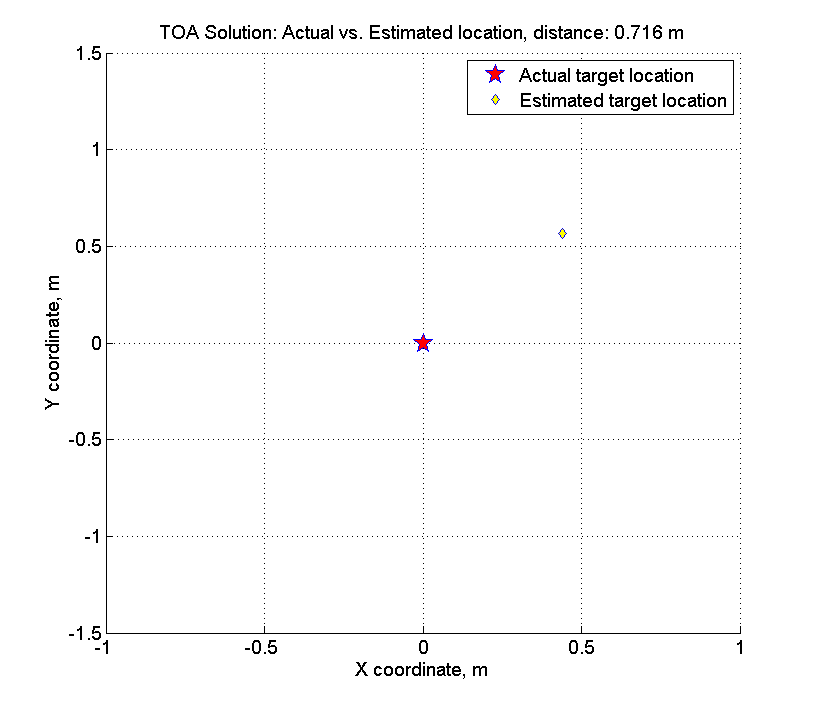
Ingatlah bahwa kami memiliki amplitudo kesalahan acak - 1% dari kisaran, rata-rata, kisarannya adalah ~ 200-400 meter, mis. amplitudo kesalahan sekitar 2-4 meter. Saat mencari solusi, kami membuat kesalahan hanya 70 sentimeter.

Sekarang, dengan analogi, kami akan mencoba menyelesaikan masalah TDOA pada data yang sama. Untuk melakukan ini, kita berpura-pura bahwa kita hanya mengetahui waktu kedatangan sinyal dari titik yang diinginkan ke titik referensi (atau sebaliknya, itu tidak masalah) - kita hanya membagi jarak kita dengan kecepatan perambatan sinyal - hanya perbedaannya dan bukan nilai absolut yang penting.

 % since TDOA works with time difference of arriaval, % we must recalculate base point's distances to times base_points(N,4) = base_points(N,4) / propagation_velocity; base_lines = Nav_build_base_lines(base_points, propagation_velocity); 

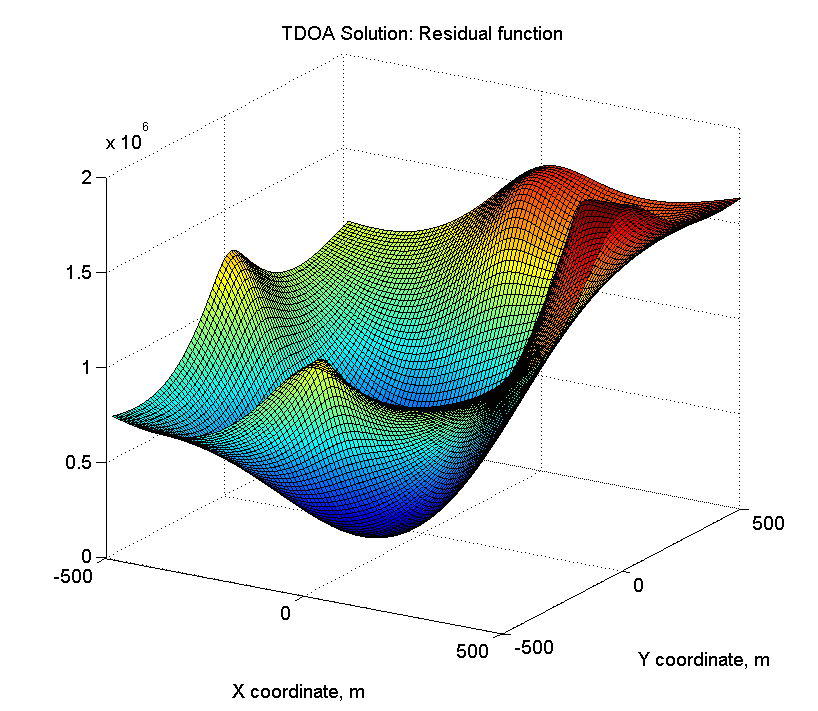
Bangun dan gambarkan permukaan kesalahan:

 error_surface_tdoa = zeros(n_tiles, n_tiles); for t_x = 1:n_tiles for t_y = 1:n_tiles error_surface_tdoa(t_x, t_y) = Nav_eps_tdoa3d(base_lines,... t_x * tile_size_m - area_width_m / 2,... t_y * tile_size_m - area_width_m / 2,... actual_target_z); end end figure surf(surf_a, surf_a, error_surface_tdoa); title('TDOA Solution: Residual function'); xlabel('X coordinate, m'); ylabel('Y coordinate, m'); view(45, 15); 

Ternyata sesuatu seperti ini:



Dan pemandangan dari atas dengan titik referensi, posisi nyata dan dihitung dari titik yang diinginkan:



Dan secara lebih rinci, perbedaan antara lokasi nyata dan yang dihitung:



Dalam kasus khusus ini, solusi TDOA ternyata lebih baik daripada solusi TOA - kesalahan absolutnya adalah 0,3 meter.

Bagus dalam model - Anda selalu tahu persis di mana titik yang diinginkan sebenarnya berada. Lebih buruk di udara - mungkin ada beberapa sudut pandang, di bawah air Anda baru saja menghitung sesuatu dan itu saja - dalam 99% kasus, untuk menghitung penyimpangan dari lokasi aktual, itu (lokasi ini) juga harus dihitung terlebih dahulu.

Sekarang, sebagai kesimpulan, kami akan menggabungkan pengetahuan baru kami tentang tugas geodetik dan navigasi.

Akord terakhir

Sedekat mungkin dengan situasi di kehidupan nyata:

• Misalkan titik referensi kami memiliki penerima GNSS bawaan dan kami hanya tahu koordinat geografisnya
• koordinat vertikal tidak diketahui oleh kami (Masalah 3D)
• kami hanya mengukur waktu kedatangan sinyal dari titik referensi pada yang diinginkan atau sebaliknya

Situasi ini dijelaskan dalam tes terbaru di ketiga implementasi. Entah bagaimana saya merampas Rust, dan saya akan menganalisis contoh terakhir tentangnya.

Jadi, tes terbaru di perpustakaan. Sebagai titik koordinat yang diinginkan, saya memilih tempat di taman, tempat saya sering berjalan bersama anjing.

 #[test] fn test_tdoa_locate_3d() { let el: Ellipsoid = Ellipsoid::from_descriptor(&WGS84_ELLIPSOID_DESCRIPTOR); let base_number = 4; // 4   let start_base_z_m: f64 = 1.5; //  Z     let base_z_step_m = 5.0; //        5  let actual_target_lat_deg: f64 = 48.513724 // singed degrees let actual_target_lon_deg: f64 = 44.553248; // signed degrees let actual_target_z_m: f64 = 25.0; // meters - ,    ! // generate base points via Vincenty equations let mut base_points = Vec::new(); let start_dst_projection_m = 500.0; //      500  let dst_inc_step_m = 50.0; //   -  50   // azimuth step let azimuth_step_rad = PI2 / base_number as f64; //     let actual_target_lat_rad = actual_target_lat_deg.to_radians(); let actual_target_lon_rad = actual_target_lon_deg.to_radians(); // signal propagation speed let velocity_mps = 1450.0; // m/s,        //     for base_idx in 0..base_number { //        let dst_projection_m = start_dst_projection_m + dst_inc_step_m * base_idx as f64; //       let azimuth_rad = azimuth_step_rad * base_idx as f64; //        Vincenty let vd_result = vincenty_direct(actual_target_lat_rad, actual_target_lon_rad, azimuth_rad, dst_projection_m, &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); //   Z let base_z_m = start_base_z_m + base_z_step_m * base_idx as f64; //        let dz_m = actual_target_z_m - base_z_m; //      let slant_range_m = (dst_projection_m * dst_projection_m + dz_m * dz_m).sqrt(); //   .          Rust   ! base_points.push((vd_result.0.to_degrees(), vd_result.1.to_degrees(), base_z_m, slant_range_m / velocity_mps)); } //     -   NAN- let lat_prev_deg = f64::NAN; let lon_prev_deg = f64::NAN; let prev_z_m = f64::NAN; //   let tdoa_3d_result = tdoa_locate_3d(&base_points, lat_prev_deg, lon_prev_deg, prev_z_m, NLM_DEF_IT_LIMIT, NLM_DEF_PREC_THRLD, 10.0, &el, velocity_mps); //          let vi_result = vincenty_inverse(actual_target_lat_rad, actual_target_lon_rad, tdoa_3d_result.0.to_radians(), tdoa_3d_result.1.to_radians(), &el, VNC_DEF_EPSILON, VNC_DEF_IT_LIMIT); assert!(vi_result.0 < start_dst_projection_m * 0.01, "Estimated location is farer than limit (1%): {}", vi_result.0); assert_approx_eq!(tdoa_3d_result.2, actual_target_z_m, start_dst_projection_m * 0.05); assert!(tdoa_3d_result.3 < start_dst_projection_m * 0.01, "Residual function greater than limit (1%): {}", tdoa_3d_result.3); assert!(tdoa_3d_result.4 < NLM_DEF_IT_LIMIT, "Method did not converge: iterations limit exeeded {}", tdoa_3d_result.4); } 

Sebagai hasilnya, kami memiliki:
Lokasi Nyata (Lat, Lon, Z): 48.513724 44.553248 25
Posisi terhitung (Lat, Lon, Z): 48.513726 44.553252 45.6
Jarak antar titik di permukaan (m): 0.389
Perbedaan dalam koordinat Z (l): 20,6

Pertandingan "plan" sangat baik, kesalahannya hanya 40 sentimeter, dan koordinat vertikal adalah 20 meter. Mengapa ini terjadi, saya sarankan pembaca berpikir =)

PS

Perpustakaan yang dijelaskan adalah proyek murni pendidikan, yang saya rencanakan untuk dikembangkan dan diisi lebih lanjut. Rencana tersebut termasuk implementasi dalam C dan penulisan dokumentasi yang komprehensif.

Atas hal ini, izinkan saya untuk pergi, terima kasih atas perhatian Anda.Saya akan sangat senang dengan umpan balik.
Semoga artikel dan pustaka akan bermanfaat.
Laporkan segala kesalahan (gramatikal dan logis) - Saya akan memperbaikinya.

PPS

Untuk berjaga-jaga, berikut ini tautan ke penerjemah Matlab / Octave online, yang saya gunakan sendiri:

• Penyusun Oktaf online
• Oktaf online
• GNU Octave