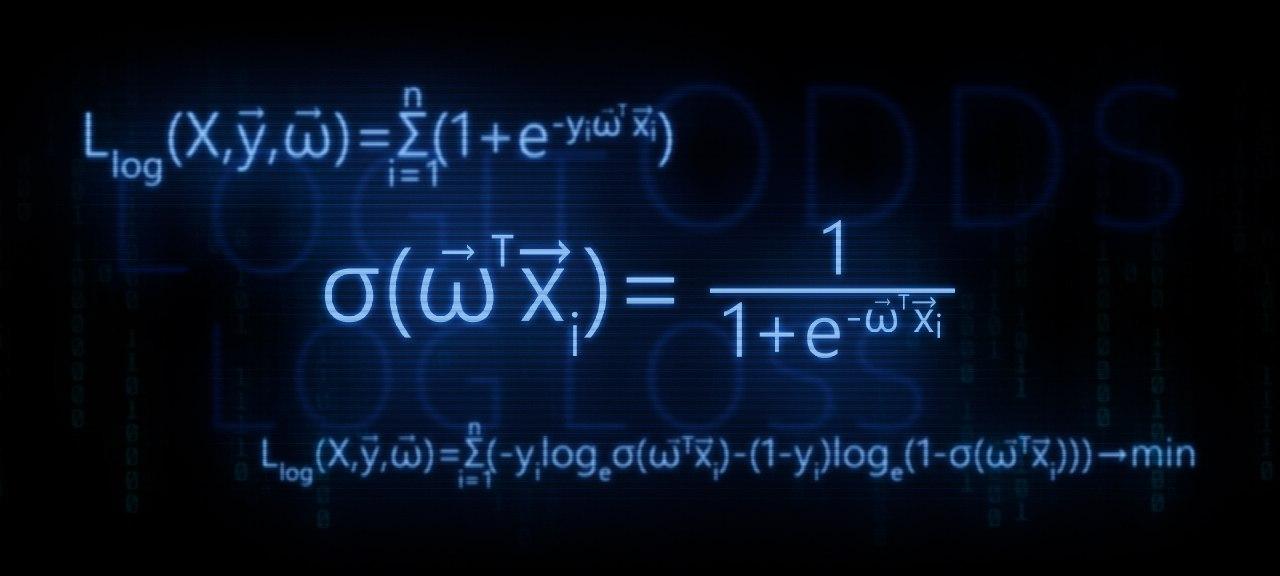
Dalam artikel ini, kita akan menganalisis perhitungan teoritis dari konversi
fungsi regresi linier ke fungsi transformasi log terbalik (dengan kata lain, fungsi respons logistik) . Kemudian, dengan menggunakan arsenal dari
metode kemungkinan maksimum , sesuai dengan model regresi logistik, kami menurunkan fungsi kerugian
Logistic Loss , atau dengan kata lain, kami menentukan fungsi dengan mana parameter dari vektor bobot dipilih dalam model regresi logistik
v e c w .
Garis besar artikel:
- Mari kita ulangi tentang hubungan langsung antara dua variabel
- Kami mengidentifikasi kebutuhan untuk mengkonversi fungsi regresi linier f ( w , x i ) = v e c w T v e c x i ke fungsi respons logistik s i g m a ( v e c w T v e c x i ) = f r a c 1 1 + e - v e c w T v e c x i $
- Kami melakukan transformasi dan mendapatkan fungsi respons logistik
- Mari kita coba memahami mengapa metode kuadrat terkecil buruk ketika memilih parameter v e c w Fitur Kehilangan Logistik
- Kami menggunakan metode kemungkinan maksimum untuk menentukan fungsi pemilihan parameter v e c w :
5.1. Kasus 1: Fungsi Kehilangan Logistik untuk objek dengan penunjukan kelas 0 dan 1 :
Llog(X, vecy, vecw)= jumlah limitni=1(−yi mkern2muloge mkern5mu sigma( vecwT vecxi)−(1−yi) mkern2muloge mkern5mu(1− sigma( vecwT vecxi))) rightarrowmin
5.2. Kasus 2: Fungsi Kehilangan Logistik untuk objek dengan penunjukan kelas -1 dan +1 :
Llog(X, vecy, vecw)= jumlah limitni=1 mkern2muloge mkern5mu(1+e−yi vecwT vecxi) rightarrowmin
Artikel ini penuh dengan contoh sederhana di mana semua perhitungan mudah dilakukan secara verbal atau di atas kertas, dalam beberapa kasus kalkulator mungkin diperlukan. Jadi bersiap-siaplah :)
Artikel ini lebih ditargetkan pada para ahli data dengan tingkat pengetahuan awal dalam dasar-dasar pembelajaran mesin.
Artikel ini juga akan menyediakan kode untuk menggambar grafik dan perhitungan. Semua kode ditulis dengan
python 2.7 . Saya akan menjelaskan di muka tentang "kebaruan" dari versi yang digunakan - ini adalah salah satu syarat untuk mengambil kursus terkenal dari
Yandex pada platform online yang tidak kalah terkenal untuk
Coursera pendidikan online, dan, seperti yang Anda duga, materi disiapkan berdasarkan kursus ini.
01. Garis lurus
Cukup masuk akal untuk mengajukan pertanyaan - di mana hubungan langsung dan regresi logistik?
Semuanya sederhana! Regresi logistik adalah salah satu model yang termasuk dalam classifier linier. Dengan kata sederhana, tujuan dari classifier linear adalah untuk memprediksi nilai target
y dari variabel (regressor)
X . Diyakini bahwa hubungan antara tanda-tanda
X dan nilai target
y linier. Karenanya nama classifier itu sendiri linear. Secara umum, model regresi logistik didasarkan pada asumsi bahwa ada hubungan linier antara fitur
X dan nilai target
y . Ini dia - koneksi.
Studio adalah contoh pertama, dan memang demikian, tentang ketergantungan langsung dari jumlah yang dipelajari. Dalam proses mempersiapkan artikel, saya menemukan contoh yang sudah
sakit tenggorokan - ketergantungan kekuatan arus pada tegangan
("Analisis Regresi Terapan", N. Draper, G. Smith) . Di sini kita akan mempertimbangkannya juga.
Sesuai dengan
hukum Ohm:I=U/R dimana
I - kekuatan saat ini
U - tegangan
R - resistensi.
Jika kita tidak tahu
hukum Ohm , kita dapat menemukan ketergantungan secara empiris dengan mengubah
U dan mengukur
I sambil mendukung
R diperbaiki. Maka kita akan melihat grafik ketergantungan
I dari
U memberikan garis lurus yang melewati titik asal. Kami mengatakan "lebih atau kurang", karena, meskipun ketergantungan sebenarnya akurat, pengukuran kami mungkin mengandung kesalahan kecil, dan karena itu titik-titik pada grafik mungkin tidak jatuh tepat pada garis, tetapi akan tersebar secara acak di sekitarnya.
Bagan 1 “Ketergantungan
I dari
U "
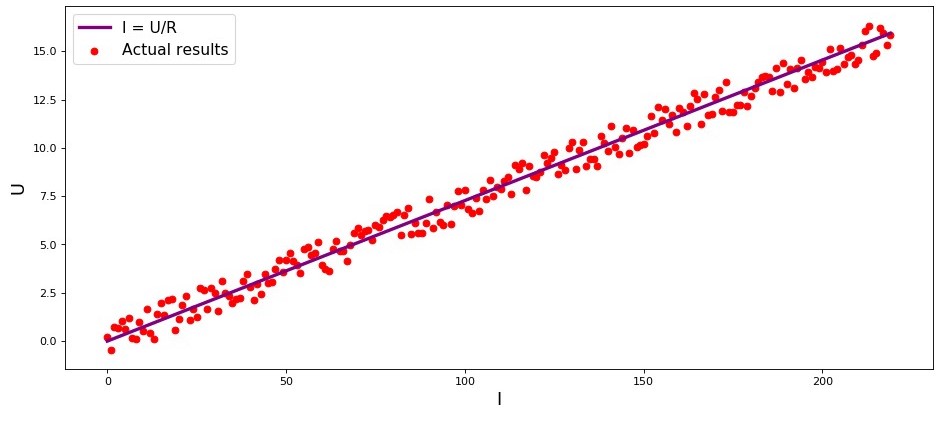
Grafik Rendering Codeimport matplotlib.pyplot as plt %matplotlib inline import numpy as np import random R = 13.75 x_line = np.arange(0,220,1) y_line = [] for i in x_line: y_line.append(i/R) y_dot = [] for i in y_line: y_dot.append(i+random.uniform(-0.9,0.9)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(x_line,y_line,color = 'purple',lw = 3, label = 'I = U/R') plt.scatter(x_line,y_dot,color = 'red', label = 'Actual results') plt.xlabel('I', size = 16) plt.ylabel('U', size = 16) plt.legend(prop = {'size': 14}) plt.show()
02. Perlunya transformasi persamaan regresi linier
Pertimbangkan contoh lain. Bayangkan kita bekerja di bank dan kita dihadapkan dengan tugas menentukan probabilitas pembayaran pinjaman oleh peminjam, tergantung pada beberapa faktor. Untuk menyederhanakan tugas, kami hanya mempertimbangkan dua faktor: gaji bulanan peminjam dan pembayaran bulanan untuk pembayaran kembali pinjaman.
Tugas ini sangat kondisional, tetapi dengan contoh ini kita dapat memahami mengapa tidak cukup menggunakan
fungsi regresi linier untuk menyelesaikannya, dan kita juga akan menemukan transformasi apa dengan fungsi yang perlu dilakukan.
Kami kembali misalnya. Dipahami bahwa semakin tinggi gaji, semakin banyak peminjam akan dapat mengarahkan setiap bulan untuk membayar kembali pinjaman. Pada saat yang sama, untuk kisaran gaji tertentu, ketergantungan ini akan cukup linier untuk dirinya sendiri. Misalnya, ambil kisaran gaji dari 60.000 hingga 200.000 dan anggaplah bahwa dalam kisaran gaji yang ditunjukkan, ketergantungan pada ukuran pembayaran bulanan pada jumlah gaji adalah linier. Misalkan, untuk kisaran upah yang ditentukan, terungkap bahwa rasio gaji terhadap pembayaran tidak dapat jatuh di bawah 3 dan bahwa peminjam masih harus memiliki cadangan 5.000. Dan hanya dalam kasus ini, kami akan menganggap bahwa peminjam akan mengembalikan pinjaman ke bank. Kemudian, persamaan regresi linier berbentuk:
f(w,xi)=w0+w1xi1+w2xi2,dimana
w0=−5.000 ,
w1=1 ,
w2=−3 ,
xi1 -
gaji i peminjam
xi2 -
pembayaran pinjaman i peminjam.
Mengganti pembayaran gaji dan pinjaman dengan parameter tetap dalam persamaan
vecw Anda dapat memutuskan apakah akan memberikan atau menolak pinjaman.
Ke depan, kami mencatat bahwa, untuk parameter yang diberikan
vecw fungsi regresi linier yang digunakan dalam
fungsi respons logistik akan menghasilkan nilai besar yang menyulitkan untuk menghitung probabilitas pembayaran kembali pinjaman. Karena itu, diusulkan untuk mengurangi koefisien kami, katakanlah, 25.000 kali. Dari konversi ini menjadi rasio, keputusan untuk memberikan pinjaman tidak akan berubah. Mari kita ingat momen ini untuk masa depan, dan sekarang untuk membuatnya lebih jelas apa yang kita bicarakan, kita akan mempertimbangkan situasi dengan tiga peminjam potensial.
Tabel 1 "Calon peminjam"
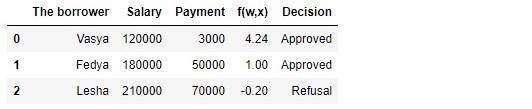
Kode untuk menghasilkan tabel import pandas as pd r = 25000.0 w_0 = -5000.0/r w_1 = 1.0/r w_2 = -3.0/r data = {'The borrower':np.array(['Vasya', 'Fedya', 'Lesha']), 'Salary':np.array([120000,180000,210000]), 'Payment':np.array([3000,50000,70000])} df = pd.DataFrame(data) df['f(w,x)'] = w_0 + df['Salary']*w_1 + df['Payment']*w_2 decision = [] for i in df['f(w,x)']: if i > 0: dec = 'Approved' decision.append(dec) else: dec = 'Refusal' decision.append(dec) df['Decision'] = decision df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision']]
Menurut tabel tersebut, Vasya, dengan gaji 120.000, ingin mendapatkan pinjaman untuk membayarnya pada 3.000 setiap bulan. Kami memutuskan bahwa untuk menyetujui pinjaman, gaji Vasya harus tiga kali lipat dari pembayaran, dan masih ada 5.000 P. Vasya memenuhi persyaratan ini:
120.000−3∗3.000−5.000=106.000 . Bahkan ada 106.000 P. Terlepas dari kenyataan bahwa ketika menghitung
f(w,xi) kami mengurangi peluang
vecw 25.000 kali, hasilnya sama - pinjaman bisa disetujui. Fedya juga akan menerima pinjaman, tetapi Lesha, meskipun faktanya ia paling banyak menerima, harus menahan nafsu makan.
Mari kita buat jadwal untuk kasus ini.
Bagan 2 "Klasifikasi peminjam"
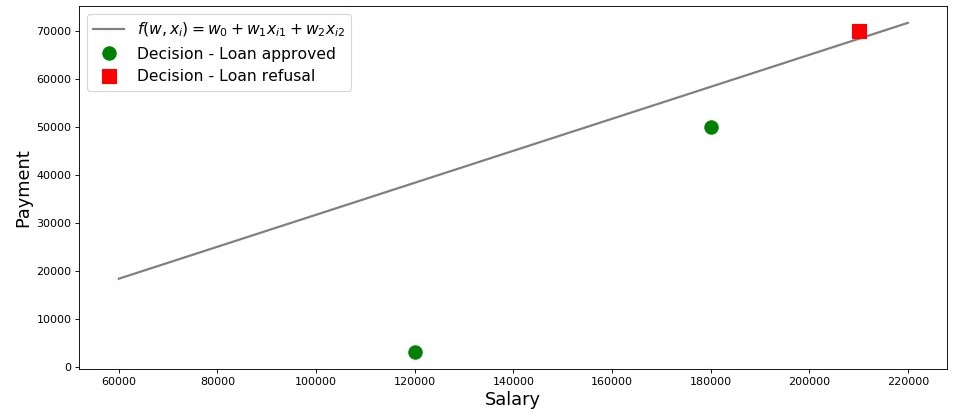
Kode untuk merencanakan salary = np.arange(60000,240000,20000) payment = (-w_0-w_1*salary)/w_2 fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(salary, payment, color = 'grey', lw = 2, label = '$f(w,x_i)=w_0 + w_1x_{i1} + w_2x_{i2}$') plt.plot(df[df['Decision'] == 'Approved']['Salary'], df[df['Decision'] == 'Approved']['Payment'], 'o', color ='green', markersize = 12, label = 'Decision - Loan approved') plt.plot(df[df['Decision'] == 'Refusal']['Salary'], df[df['Decision'] == 'Refusal']['Payment'], 's', color = 'red', markersize = 12, label = 'Decision - Loan refusal') plt.xlabel('Salary', size = 16) plt.ylabel('Payment', size = 16) plt.legend(prop = {'size': 14}) plt.show()
Jadi, jalur kita, dibangun sesuai dengan fungsinya
f(w,xi)=w0+w1xi1+w2xi2 , memisahkan peminjam "buruk" dari "baik". Para peminjam yang keinginannya tidak sesuai dengan kemampuan mereka berada di atas garis langsung (Lesha), mereka yang mampu membayar pinjaman sesuai dengan parameter model kami berada di bawah garis langsung (Vasya dan Fedya). Kalau tidak, kita dapat mengatakan ini - baris kami membagi peminjam menjadi dua kelas. Kami menyatakan mereka sebagai berikut: ke kelas
+1 mengklasifikasikan peminjam yang cenderung membayar pinjaman ke kelas
−1 atau
0 kami akan menugaskan peminjam yang kemungkinan besar tidak akan mampu membayar pinjaman.
Ringkas kesimpulan dari contoh sederhana ini. Ambil satu poin
M(x1,x2) dan, menggantikan koordinat titik dalam persamaan garis yang sesuai
f(w,xi)=w0+w1xi1+w2xi2 , pertimbangkan tiga opsi:
- Jika intinya ada di bawah garis, dan kita menugaskannya ke kelas +1 , maka nilai fungsi f(w,xi)=w0+w1xi1+w2xi2 akan positif dari 0 sebelumnya + infty . Jadi kita dapat mengasumsikan bahwa kemungkinan pembayaran kembali pinjaman ada di dalam (0,5,1] . Semakin besar nilai fungsi, semakin tinggi probabilitasnya.
- Jika titik di atas garis dan kami menghubungkannya ke kelas −1 atau 0 , maka nilai fungsi akan menjadi negatif dari 0 sebelumnya − infty . Maka kita akan mengasumsikan bahwa kemungkinan pembayaran utang ada di dalam [0,0.5) dan, semakin besar nilai fungsi modulo, semakin tinggi kepercayaan diri kami.
- Intinya adalah pada garis lurus, di perbatasan antara dua kelas. Dalam hal ini, nilai fungsi f(w,xi)=w0+w1xi1+w2xi2 akan sama 0 dan probabilitas pembayaran pinjaman sama dengan 0,5 .
Sekarang, bayangkan kita tidak memiliki dua faktor, tetapi puluhan, peminjam bukan tiga, tetapi ribuan. Maka alih-alih garis lurus kita akan memiliki bidang
m-dimensi dan koefisien
w kami akan diambil bukan dari plafon, tetapi ditarik sesuai dengan semua aturan, tetapi berdasarkan akumulasi data pada peminjam yang mengembalikan atau tidak mengembalikan pinjaman. Dan sungguh, ingatlah, kami sekarang memilih peminjam dengan rasio yang sudah dikenal
w . Bahkan, tugas model regresi logistik adalah untuk menentukan parameter
w di mana nilai fungsi kerugian
Logistic Loss akan cenderung minimum. Tapi bagaimana vektor dihitung
vecw , kami masih mencari tahu di bagian 5 artikel. Sementara itu, kami kembali ke tanah yang dijanjikan - kepada bankir kami dan tiga kliennya.
Berkat fungsinya
f(w,xi)=w0+w1xi1+w2xi2 kita tahu siapa yang bisa diberi pinjaman, dan siapa yang perlu ditolak. Tetapi Anda tidak dapat pergi ke direktur dengan informasi seperti itu, karena mereka ingin mendapatkan kemungkinan pembayaran kembali pinjaman dari setiap peminjam dari kami. Apa yang harus dilakukan Jawabannya sederhana - kita perlu mengubah fungsinya
f(w,xi)=w0+w1xi1+w2xi2 yang nilainya terletak pada kisaran
(− infty,+ infty) pada fungsi yang nilainya akan berada dalam kisaran
[0,1] . Dan ada fungsi seperti itu, itu disebut
fungsi respon logistik atau konversi reverse-logit . Bertemu:
sigma( vecwT vecxi)= frac11+e− vecwT vecxi$
Mari kita lihat langkah-langkah untuk mendapatkan
fungsi respons logistik . Perhatikan bahwa kita akan melangkah ke arah yang berlawanan, mis. kami berasumsi bahwa kami tahu nilai probabilitas, yang terletak pada kisaran dari
0 sebelumnya
1 dan kemudian kita akan "memutar" nilai ini di seluruh rentang angka dari
− infty sebelumnya
+ infty .
03. Keluarkan fungsi respons logistik
Langkah 1. Transfer nilai probabilitas ke kisaran [0,+ infty)
Pada saat transformasi fungsi
f(w,xi)=w0+w1xi1+w2xi2 ke
fungsi respons logistik sigma( vecwT vecxi)= frac11+e vecwT vecxi$ kita akan meninggalkan analis kredit kita sendiri, dan bukannya melalui bandar taruhan. Tidak, tentu saja, kami tidak akan bertaruh, semua yang menarik minat kami di sana adalah arti dari ungkapan, misalnya, peluang 4 banding 1. Peluang yang lazim bagi semua pemain taruhan adalah rasio "sukses" dengan "kegagalan". Dalam hal probabilitas, odds adalah probabilitas dari suatu peristiwa yang terjadi dibagi dengan probabilitas bahwa peristiwa itu tidak akan terjadi. Kami menulis formula untuk peluang acara
(odds+) :
odds+= fracp+1−p+
dimana
p+ - probabilitas terjadinya suatu peristiwa,
(1−p+) - probabilitas BUKAN terjadinya suatu peristiwa
Misalnya, jika kemungkinan bahwa kuda muda, kuat, dan bersemangat tinggi, yang dijuluki "Veterok" akan mengalahkan di balapan, seorang wanita tua yang lemah dan berjuluk "Matilda" sama dengan
0,8 , maka kemungkinan keberhasilan Veterka akan
4 untuk
1(0,8/(1−0,8)) dan sebaliknya, mengetahui peluang, tidak akan sulit bagi kita untuk menghitung probabilitas
p+ :
fracp+1−p+=4 mkern15mu Longrightarrow mkern15mup+=4(1−p+) mkern15mu Longrightarrow mkern15mu5p+=4 mkern15mu Longrightarrow mkern15mup+=0,8Dengan demikian, kami telah belajar untuk "menerjemahkan" probabilitas menjadi peluang yang mengambil nilai dari
0 sebelumnya
+ infty . Mari kita mengambil satu langkah lagi dan belajar bagaimana "menerjemahkan" probabilitas ke garis bilangan bulat dari
− infty sebelumnya
+ infty .
Langkah 2. Kami menerjemahkan nilai probabilitas ke dalam rentang (− infty,+ infty)
Langkah ini sangat sederhana - kami prolog peluang berdasarkan nomor Euler
e dan dapatkan:
f(w,xi)= vecwT vecx=ln(odds+)
Sekarang kita tahu bahwa jika
p+=0,8 lalu hitung nilainya
f(w,xi) itu akan sangat sederhana dan, terlebih lagi, itu harus positif:
f(w,xi)=ln(odds+)=ln(0.8/0.2)=ln(4) kurang−lebih+1.38629 . Begitulah.
Demi rasa ingin tahu, kami memeriksa apakah
p+=0,2 maka kita berharap untuk melihat nilai negatif
f(w,xi) . Kami memeriksa:
f(w,xi)=ln(0.2/0.8)=ln(0.25) kira−kira−1.38629 . Baiklah
Sekarang kita tahu bagaimana menerjemahkan nilai probabilitas dari
0 sebelumnya
1 pada garis bilangan bulat dari
− infty sebelumnya
+ infty . Pada langkah selanjutnya, kita akan melakukan yang sebaliknya.
Sementara itu, kami mencatat bahwa sesuai dengan aturan logaritma, mengetahui nilai fungsi
f(w,xi) , Anda dapat menghitung peluang:
odds+=ef(w,xi)=e vecwT vecx
Metode penentuan peluang ini akan berguna pada langkah selanjutnya.
Langkah 3. Kami mendapatkan formula untuk menentukan p+
Jadi kami belajar, mengetahui
p+ temukan nilai fungsi
f(w,xi) . Namun, pada kenyataannya, kita membutuhkan segalanya yang sebaliknya - mengetahui nilainya
f(w,xi) untuk menemukan
p+ . Untuk melakukan ini, kita beralih ke konsep seperti fungsi kebalikan dari peluang, sesuai dengan yang:
p+= fracodds+1+odds+
Dalam artikel kami tidak akan menurunkan rumus di atas, tetapi memeriksa angka-angka dari contoh di atas. Kita tahu bahwa dengan odds 4 banding 1 (
odds+=$ ), probabilitas suatu peristiwa yang terjadi adalah 0,8 (
p+=0,8 ) Mari kita lakukan substitusi:
p+= frac41+4=0,8 . Ini bertepatan dengan perhitungan kami yang dilakukan sebelumnya. Kami melanjutkan.
Pada langkah terakhir, kami menyimpulkan itu
odds+=e vecwT vecx , yang berarti bahwa Anda dapat membuat substitusi dalam fungsi odds terbalik. Kami mendapatkan:
p+= frace vecwT vecx1+e vecwT vecx
Bagi pembilang dan penyebut dengan
e vecwT vecx lalu:
p+= frac11+e− vecwT vecx= sigma( vecwT vecx)
Untuk setiap pemadam kebakaran, untuk memastikan bahwa kami tidak melakukan kesalahan di mana pun, kami akan melakukan satu pemeriksaan kecil lagi. Pada langkah 2, kita cocok untuk
p+=0,8 ditentukan itu
f(w,xi) approx+1.38629 . Kemudian, gantikan nilainya
f(w,xi) dalam fungsi respons logistik, kami berharap mendapatkan
p+=0,8 . Pengganti dan dapatkan:
p+= frac11+e−1.38629=0,8Selamat, pembaca yang budiman, kami baru saja mengembangkan dan menguji fungsi respons logistik. Mari kita lihat grafik fungsi.
Bagan 3 “Fungsi Respons Logistik”

Kode untuk merencanakan import math def logit (f): return 1/(1+math.exp(-f)) f = np.arange(-7,7,0.05) p = [] for i in f: p.append(logit(i)) fig, axes = plt.subplots(figsize = (14,6), dpi = 80) plt.plot(f, p, color = 'grey', label = '$ 1 / (1+e^{-w^Tx_i})$') plt.xlabel('$f(w,x_i) = w^Tx_i$', size = 16) plt.ylabel('$p_{i+}$', size = 16) plt.legend(prop = {'size': 14}) plt.show()
Dalam literatur, Anda juga dapat menemukan nama fungsi ini sebagai
fungsi sigmoid . Grafik dengan jelas menunjukkan bahwa perubahan utama dalam kemungkinan memiliki suatu objek ke kelas terjadi dalam kisaran yang relatif kecil
f(w,xi) suatu tempat dari
−4 sebelumnya
+4 .
Saya mengusulkan untuk kembali ke analis kredit kami dan membantunya menghitung kemungkinan pembayaran kembali pinjaman, jika tidak ia berisiko dibiarkan tanpa bonus :)
Tabel 2 "Calon peminjam"
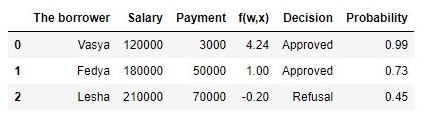
Kode untuk menghasilkan tabel proba = [] for i in df['f(w,x)']: proba.append(round(logit(i),2)) df['Probability'] = proba df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision', 'Probability']]
Jadi, kami menentukan probabilitas pembayaran kembali pinjaman. Secara keseluruhan, ini tampaknya benar.
Memang, probabilitas bahwa Vasya dengan gaji 120.000 akan dapat memberikan 3.000 bulanan ke bank mendekati 100%. Ngomong-ngomong, kita harus memahami bahwa bank dapat memberikan pinjaman kepada Lesha juga jika kebijakan bank memberikan, misalnya, untuk memberi pinjaman kepada pelanggan dengan kemungkinan pembayaran kembali pinjaman lebih dari, katakanlah, 0,3. Hanya dalam kasus ini, bank akan membentuk cadangan yang lebih besar untuk kemungkinan kerugian.
Juga harus dicatat bahwa rasio gaji terhadap pembayaran minimal 3 dan dengan margin 5.000 diambil dari langit-langit. Karena itu, kami tidak dapat menggunakan vektor bobot dalam bentuk aslinya
vecw=(−5000,1,−3) . Kami perlu sangat mengurangi koefisien, dan dalam hal ini kami membagi masing-masing koefisien dengan 25.000, yaitu, pada kenyataannya, kami menyesuaikan hasilnya. Tetapi ini dilakukan dengan sengaja untuk menyederhanakan pemahaman materi pada tahap awal. Dalam kehidupan, kita tidak perlu menemukan dan menyesuaikan koefisien, tetapi untuk menemukannya. Hanya di bagian artikel selanjutnya kita akan mendapatkan persamaan yang parameternya dipilih
vecw .
04. Metode kuadrat terkecil untuk menentukan vektor bobot vecw dalam fungsi respons logistik
Kita sudah tahu metode seperti itu untuk memilih vektor bobot
vecw sebagai
metode kuadrat terkecil (OLS) dan, pada kenyataannya, mengapa kita tidak menggunakannya dalam masalah klasifikasi biner? Memang, tidak ada yang mencegah penggunaan
MNC , hanya metode ini dalam masalah klasifikasi memberikan hasil yang kurang akurat daripada
Kehilangan Logistik . Ada pembenaran teoretis untuk ini. Mari kita mulai dengan melihat satu contoh sederhana.
Misalkan model kami (menggunakan
MSE dan
Logistic Loss ) sudah memulai pemilihan vektor bobot
vecw dan kami menghentikan perhitungan pada beberapa langkah. Tidak masalah, di tengah, di akhir atau di awal, yang utama adalah bahwa kita sudah memiliki beberapa nilai vektor bobot dan anggap, pada langkah ini, vektor bobot
vecw untuk kedua model tidak memiliki perbedaan. Kemudian kami mengambil bobot yang diperoleh dan menggantinya ke
fungsi respons logistik (
frac11+e− vecwT vecx ) untuk beberapa objek yang termasuk dalam kelas
+1 . Kami akan menyelidiki dua kasus ketika, sesuai dengan vektor bobot yang dipilih, model kami sangat keliru dan sebaliknya - model sangat yakin bahwa objek tersebut termasuk kelas.
+1 . Mari kita lihat denda apa yang akan "dikeluarkan" saat menggunakan
MNC dan
Logistic Loss .
Kode untuk menghitung denda tergantung pada fungsi kerugian yang digunakan Kasing dengan kesalahan kotor - model mengklasifikasikan objek
+1 dengan probabilitas 0,01
Penalti saat menggunakan
OLS adalah:
MSE=(y−p+)=(1−0.01)2=0,9801Penalti saat menggunakan
Kehilangan Logistik adalah:
LogKehilangan=loge(1+e−yf(w,x))=loge(1+e−1(−4.595...)) kira−kira4,605Kasus dengan kepastian yang kuat - model mengklasifikasikan objek
+1 dengan probabilitas 0,99
Penalti saat menggunakan
OLS adalah:
MSE=(1−0.99)2=$0,000Penalti saat menggunakan
Kehilangan Logistik adalah:
LogKehilangan=loge(1+e−4.595...) sekitar0,01Contoh ini menggambarkan dengan baik bahwa dengan kesalahan kotor, fungsi
Kehilangan Log kehilangan model secara signifikan lebih dari
MSE . Sekarang mari kita memahami apa saja prasyarat teoritis untuk menggunakan fungsi
Kehilangan Log Kehilangan dalam masalah klasifikasi.
05. Metode Kredibilitas Maksimum dan Regresi Logistik
Seperti yang dijanjikan di awal, artikel ini dipenuhi dengan contoh-contoh sederhana. Di studio, contoh lain dan tamu lama adalah peminjam bank: Vasya, Fedya, dan Lesha.
Untuk setiap pemadam kebakaran, sebelum mengembangkan contoh, izinkan saya mengingatkan Anda bahwa dalam hidup kita berurusan dengan sampel pelatihan ribuan atau jutaan objek dengan puluhan atau ratusan tanda. Namun, di sini angkanya diambil sehingga mereka cocok dengan mudah ke kepala data pemula pemula.
Kami kembali misalnya. Bayangkan bahwa direktur bank memutuskan untuk memberikan pinjaman kepada semua yang membutuhkan, terlepas dari kenyataan bahwa algoritma menyarankan untuk tidak memberikannya kepada Lesha. Dan sudah cukup waktu berlalu dan kami menjadi tahu yang mana dari tiga pahlawan yang membayar pinjaman, dan siapa yang tidak. Apa yang diharapkan: Vasya dan Fedya melunasi pinjaman, tetapi Alex tidak. Sekarang mari kita bayangkan bahwa hasil ini akan menjadi sampel pelatihan baru bagi kita dan, pada saat yang sama, semua data tentang faktor-faktor yang mempengaruhi kemungkinan pembayaran kembali pinjaman (gaji peminjam, jumlah pembayaran bulanan) tampaknya telah menghilang. Kemudian, secara intuitif, kita dapat mengasumsikan bahwa setiap peminjam ketiga tidak mengembalikan pinjaman ke bank, atau dengan kata lain, kemungkinan pinjaman dikembalikan oleh peminjam berikutnya.
p= frac23 . Ada bukti teoritis untuk asumsi intuitif ini dan didasarkan pada
metode kemungkinan maksimum , sering disebut dalam literatur sebagai
prinsip kemungkinan maksimum .
Pertama, berkenalanlah dengan alat konseptual.
Kemungkinan
sampel adalah kemungkinan mendapatkan sampel seperti itu, untuk mendapatkan pengamatan / hasil yang tepat, yaitu. produk dari probabilitas memperoleh masing-masing hasil sampel (misalnya, pinjaman Vasya, Feday dan Lesha pada saat yang sama dilunasi atau tidak dilunasi).
Fungsi likelihood mengaitkan kemungkinan sampel dengan nilai-nilai parameter distribusi.
Dalam kasus kami, sampel pelatihan adalah skema Bernoulli umum di mana variabel acak hanya mengambil dua nilai:
1 atau
0 . Oleh karena itu, kemungkinan sampel dapat ditulis sebagai fungsi dari kemungkinan parameter
p sebagai berikut:
P( mkern5mu vecy mkern5mu| mkern5mup)= prod limit3i=1pyi(1−p)(1−yi) mkern5mu= mkern5mup1(1−p)1−1 centerdotp1(1−p)1−1 centerdotp0(1−p)1−0 mkern5mu== mkern5mup centerdotp centerdot(1−p) mkern5mu= mkern5mup2(1−p)Catatan di atas dapat diartikan sebagai berikut. Peluang bersama Vasya dan Fedya akan membayar kembali pinjaman adalah sama dengan
p centerdotp=p2 , kemungkinan bahwa Alex TIDAK akan membayar pinjaman
1−p (karena BUKAN pelunasan pinjaman), oleh karena itu, probabilitas gabungan dari ketiga peristiwa tersebut adalah
p2(1−p) .
Metode kemungkinan maksimum adalah metode untuk memperkirakan parameter yang tidak diketahui dengan memaksimalkan fungsi kemungkinan . Dalam kasus kami, kami perlu menemukan nilai seperti itup dimana P(→y|p)=p2(1−p)mencapai maksimum.Dari mana ide tersebut berasal - untuk mencari nilai parameter yang tidak diketahui di mana fungsi kemungkinan mencapai maksimum? Asal usul ide tersebut berasal dari anggapan bahwa pengambilan sampel adalah satu-satunya sumber pengetahuan tentang populasi umum yang tersedia bagi kami. Segala sesuatu yang kita ketahui tentang populasi disajikan dalam sampel. Oleh karena itu, yang dapat kami katakan adalah bahwa sampel adalah cerminan paling akurat dari populasi yang tersedia bagi kami. Oleh karena itu, kita perlu menemukan parameter di mana sampel yang tersedia menjadi yang paling memungkinkan.Jelas, kita berhadapan dengan masalah optimisasi di mana diperlukan untuk menemukan titik ekstrem dari suatu fungsi. Untuk menemukan titik ekstrem, perlu mempertimbangkan kondisi orde pertama, yaitu, untuk menyamakan turunan dari fungsi ke nol dan menyelesaikan persamaan untuk parameter yang diinginkan. Namun, pencarian turunan suatu produk dari sejumlah besar faktor dapat memakan waktu lama, sehingga ada teknik khusus untuk menghindarinya - transisi ke logaritma fungsi kemungkinan . Mengapa transisi seperti itu dimungkinkan? Kami memperhatikan fakta bahwa kami tidak mencari ekstrem fungsi itu sendiriP(→y|p) , dan titik ekstrim, yaitu, nilai parameter yang tidak diketahui p dimana P(→y|p)mencapai maksimum. Setelah transisi ke logaritma, titik ekstrem tidak berubah (walaupun ekstrem itu sendiri akan berbeda), karena logaritma adalah fungsi monoton.Mari kita, sesuai dengan yang disebutkan di atas, terus mengembangkan contoh pinjaman kami dengan Vasya, Fedi dan Lesha. Pertama, mari kita beralih ke logaritma fungsi kemungkinan :logP(→y|p)=logp2(1−p)=2logp+log(1−p)Sekarang kita dapat dengan mudah membedakan ekspresi p :
∂logP(→y|p)∂p=∂∂p(2logp+log(1−p))=2p−11−pDan akhirnya, pertimbangkan kondisi urutan pertama - kami menyamakan turunan dari fungsi ke nol:2p−11−p=0⟹2p=11−p⟹2(1−p)=p⟹p=23Dengan demikian, penilaian intuitif kami tentang kemungkinan pembayaran kembali pinjaman p=23secara teoritis dibuktikan.Hebat, tapi apa yang kita lakukan sekarang dengan informasi ini? Jika kita berasumsi bahwa setiap peminjam ketiga tidak mengembalikan uang ke bank, maka peminjam yang ketiga pasti akan bangkrut. Begitulah, tetapi hanya ketika menilai probabilitas pembayaran pinjaman sama dengan23Kami tidak memperhitungkan faktor-faktor yang mempengaruhi pelunasan pinjaman: gaji peminjam dan jumlah pembayaran bulanan. Ingatlah bahwa sebelumnya kami menghitung probabilitas pembayaran pinjaman oleh setiap klien, dengan mempertimbangkan faktor-faktor ini. Adalah logis bahwa probabilitas yang kami dapatkan berbeda dari konstanta sama dengan23 .
Mari kita tentukan kemungkinan sampel:Kode untuk menghitung kemungkinan sampel from functools import reduce def likelihood(y,p): line_true_proba = [] for i in range(len(y)): ltp_i = p[i]**y[i]*(1-p[i])**(1-y[i]) line_true_proba.append(ltp_i) likelihood = [] return reduce(lambda a, b: a*b, line_true_proba) y = [1.0,1.0,0.0] p_log_response = df['Probability'] const = 2.0/3.0 p_const = [const, const, const] print ' p=2/3:', round(likelihood(y,p_const),3) print '****************************************************************************************************' print ' p:', round(likelihood(y,p_log_response),3)
Kemungkinan pengambilan sampel dengan nilai konstan p=23 :P(→y|p)=p2(1−p)=232(1−23)≈0.148Kemungkinan pengambilan sampel dalam menghitung kemungkinan pembayaran pinjaman dengan mempertimbangkan faktor-faktor akun →x :P(→y|p)=3∏i=1pyi(1−p)(1−yi)=p11(1−p1)1−1⋅p12(1−p2)1−1⋅p03(1−p3)1−0==p1⋅p2⋅(1−p3)=0.99⋅0.73⋅(1−0.45)≈0.397Kemungkinan sampel dengan probabilitas yang dihitung tergantung pada faktor-faktor lebih tinggi dari kemungkinan dengan nilai probabilitas yang konstan. Apa yang sedang dibicarakan ini? Ini menunjukkan bahwa pengetahuan tentang faktor-faktor memungkinkan untuk memilih secara lebih akurat kemungkinan pembayaran kembali pinjaman untuk setiap klien. Oleh karena itu, ketika mengeluarkan pinjaman lain, akan lebih tepat untuk menggunakan model untuk menilai probabilitas pembayaran utang yang diusulkan pada akhir bagian ke-3 dari artikel tersebut.Tapi kemudian, jika kita perlu memaksimalkan fungsi kemungkinan sampel, lalu mengapa tidak menggunakan beberapa algoritma yang akan memberikan probabilitas untuk Vasya, Fedi dan Lesha, misalnya, masing-masing sama dengan 0,99, 0,99 dan 0,01. Mungkin algoritma semacam itu akan menunjukkan dirinya dengan baik dalam sampel pelatihan, karena itu akan membawa nilai kemungkinan sampel lebih dekat ke1, tetapi, pertama, algoritma semacam itu kemungkinan besar akan mengalami kesulitan dengan kemampuan generalisasi, dan kedua, algoritma ini pasti tidak akan linier. Dan jika metode berurusan dengan pelatihan ulang (kemampuan generalisasi yang sama lemahnya) jelas tidak termasuk dalam rencana artikel ini, maka mari kita lihat paragraf kedua secara lebih rinci. Untuk melakukan ini, jawab saja pertanyaan sederhana. Bisakah probabilitas membayar pinjaman kepada Vasya dan Feday sama, dengan mempertimbangkan faktor-faktor yang diketahui oleh kami? Dari sudut pandang logika suara, tentu saja tidak, itu tidak bisa. Jadi, Vasya akan memberikan 2,5% dari gajinya per bulan untuk membayar pinjaman, dan Fedya - hampir 27,8%. Juga pada grafik 2 "Klasifikasi pelanggan" kita melihat bahwa Vasya jauh lebih jauh dari garis yang memisahkan kelas daripada Fedya. Dan akhirnya, kita tahu fungsinyaf(w,x)=w0+w1x1+w2x2untuk Vasya dan Fedi dibutuhkan arti yang berbeda: 4.24 untuk Vasya dan 1.0 untuk Fedi. Sekarang, jika Fedya, misalnya, mendapat pesanan lebih besar atau meminta pinjaman yang lebih kecil, maka kemungkinan melunasi pinjaman dari Vasya dan Fedi akan serupa. Dengan kata lain, hubungan linier tidak bisa dibodohi. Dan jika kita benar-benar menghitung peluangw , tetapi tidak mengambilnya dari langit-langit, kami dapat dengan aman menyatakan bahwa nilai-nilai kami w sebaiknya Anda menilai kemungkinan pelunasan pinjaman oleh masing-masing peminjam, tetapi karena kami sepakat untuk mempertimbangkan bahwa penentuan koefisien wdilakukan sesuai dengan semua aturan, maka kami akan mempertimbangkannya begitu - koefisien kami memungkinkan kami untuk memberikan perkiraan probabilitas yang lebih baik :)Namun, kami terganggu. Pada bagian ini, kita perlu memahami bagaimana vektor bobot ditentukan→w, yang diperlukan untuk menilai kemungkinan pengembalian pinjaman oleh setiap peminjam.Ringkas secara singkat arsenal apa yang kita cari peluangnyaw :
1. Kami berasumsi bahwa hubungan antara variabel target (nilai perkiraan) dan faktor yang mempengaruhi hasilnya adalah linear. Untuk alasan ini, fungsi regresi linier formulir digunakan.f(w,x)=→wTX yang garisnya membagi objek (klien) ke dalam kelas +1 dan −1 atau 0(pelanggan yang mampu membayar pinjaman dan tidak mampu). Dalam kasus kami, persamaan memiliki bentukf(w,x)=w0+w1x1+w2x2 .
2. Kami menggunakan fungsi transformasi log terbalik dari formulirp+=11+e−→wT→x=σ(→wT→x) untuk menentukan probabilitas bahwa suatu objek milik kelas +1 .
3. Kami menganggap sampel pelatihan kami sebagai implementasi dari skema Bernoulli yang digeneralisasi , yaitu, untuk setiap objek dihasilkan variabel acak, yang dengan probabilitasp (sendiri untuk setiap objek) mengambil nilai 1 dan dengan probabilitas (1–p)- 0.4. Kita tahu bahwa kita perlu memaksimalkan fungsi kemungkinan sampel , dengan mempertimbangkan faktor-faktor yang diterima, sehingga sampel yang ada menjadi yang paling mungkin. Dengan kata lain, kita perlu memilih parameter seperti itu di mana sampel akan menjadi yang paling masuk akal. Dalam kasus kami, parameter yang dipilih adalah probabilitas pelunasan pinjamanp , yang pada gilirannya tergantung pada koefisien yang tidak diketahui w .
Jadi kita perlu menemukan vektor bobot seperti itu →wdi mana kemungkinan sampel akan maksimal.5. Kami tahu bahwa untuk memaksimalkan fungsi kemungkinan sampel, Anda dapat menggunakan metode kemungkinan maksimum . Dan kita tahu semua trik untuk bekerja dengan metode ini.Berikut ini adalah multi-jalur :)Dan sekarang ingat bahwa pada awal artikel kami ingin menurunkan dua jenis fungsi kerugian Kehilangan Logistik , tergantung pada bagaimana kelas objek ditetapkan. Kebetulan dalam masalah klasifikasi dengan dua kelas, kelas dilambangkan sebagai+1 dan 0 atau −1 .
Tergantung pada penunjukannya, output akan memiliki fungsi kerugian yang sesuai.Kasus 1. Klasifikasi objek menjadi +1 dan 0
Sebelumnya, dalam menentukan kemungkinan sampel di mana kemungkinan pelunasan hutang oleh peminjam dihitung berdasarkan faktor dan koefisien yang ditentukan w , kami menerapkan rumus:P(→y|p)=3∏i=1pyi(1−p)(1−yi)Sebenarnya piMerupakan nilai dari fungsi respons logistik p+=11+e−→wT→x=σ(→wT→x) untuk vektor bobot yang diberikan →wMaka tidak ada yang mencegah kita dari menulis fungsi kemungkinan sampel seperti ini:P(→y|σ(→wTX))=n∏i=1σ(→wT→xi)yi(1−σ(→wT→xi)(1−yi)→max
Itu terjadi bahwa kadang-kadang, untuk beberapa analis pemula, sulit untuk segera memahami bagaimana fungsi ini bekerja. Mari kita lihat 4 contoh singkat yang akan menjelaskan semuanya:1. Jikayi=+1 (mis., sesuai dengan sampel pelatihan, objek milik kelas +1), dan algoritma kami σ(→wTX)) menentukan kemungkinan mengklasifikasikan objek +1 sama dengan 0,9, maka potongan kemungkinan sampel ini akan dihitung sebagai berikut:0.91⋅(1−0.9)(1−1)=0.91⋅0.10=0.92. Jikayi=+1 , dan σ(→wTX))=0.1 , maka perhitungannya akan seperti ini:0.11⋅(1−0.1)(1−1)=0.11⋅0.90=0.13. Jikayi=0 , dan σ(→wTX))=0.1 , maka perhitungannya akan seperti ini:0.10⋅(1−0.1)(1−0)=0.10⋅0.91=0.94. Jikayi=0 , dan σ(→wTX))=0.9 , maka perhitungannya akan seperti ini:0.90⋅(1−0.9)(1−0)=0.90⋅0.11=0.1Jelas, fungsi kemungkinan akan dimaksimalkan dalam kasus 1 dan 3, atau dalam kasus umum, dengan nilai duga yang benar dari probabilitas mengklasifikasikan objek sebagai kelas. +1 .
Karena kenyataan bahwa ketika menentukan probabilitas mengklasifikasikan objek sebagai kelas +1 kita tidak tahu hanya koefisien w, maka kita akan mencari mereka. Seperti disebutkan di atas, ini adalah masalah optimisasi di mana kita pertama-tama perlu menemukan turunan dari fungsi kemungkinan sehubungan dengan vektor bobotw .
Namun, masuk akal untuk menyederhanakan tugas terlebih dahulu: kita akan mencari turunan dari logaritma fungsi kemungkinan .Llog(X,→y,→w)=n∑i=1(−yilogeσ(→wT→xi)−(1−yi)loge(1−σ(→wT→xi)))→min
Mengapa, setelah logaritma, dalam fungsi kesalahan logistik , kami mengganti tanda dengan+ pada − .
Semuanya sederhana, karena biasanya untuk meminimalkan nilai fungsi dalam masalah penilaian kualitas model, kami mengalikan sisi kanan ekspresi dengan −dan karenanya alih-alih memaksimalkan, sekarang kami meminimalkan fungsinya.Sebenarnya, sekarang, di depan mata Anda sendiri, fungsi kerugian - Kehilangan Logistik untuk pelatihan yang ditetapkan dengan dua kelas sangat menderita .+1 dan 0 .
Sekarang, untuk menemukan koefisien, kita hanya perlu mencari turunan dari fungsi kesalahan logistik dan kemudian, menggunakan metode optimasi numerik, seperti gradient descent atau stochastic gradient descent, pilih koefisien yang paling optimalw .
Tetapi, mengingat ukuran artikel yang sudah kecil, diusulkan untuk melakukan pembedaan secara mandiri atau, mungkin, ini akan menjadi topik untuk artikel berikutnya dengan banyak aritmatika tanpa contoh-contoh terperinci seperti itu.Kasus 2. Klasifikasi objek menjadi +1 dan −1
Pendekatan di sini akan sama dengan kelas 1 dan 0tetapi jalur itu sendiri ke output dari fungsi kehilangan Kehilangan Logistik akan lebih berornamen. Turun. Untuk fungsi kemungkinan, kami menggunakan operator "jika ... lalu ..." . Itu kalaui objek th milik kelas +1 , kemudian untuk menghitung kemungkinan sampel, kami menggunakan probabilitas p jika objek milik kelas −1 , maka dalam pengganti verisimilitude (1−p) .
Seperti inilah fungsi kemungkinannya:P(→y|σ(→wTX))=n∏i=1σ(→wT→xi)[yi=+1](1−σ(→wT→xi)[yi=−1])→max
Kami akan menulis dengan jari bagaimana ini bekerja. Pertimbangkan 4 kasus:1. Jikayi=+1 dan σ(→wT→xi)=0.9 , maka dalam verisimilitude sampel "pergi" 0.92. Jikayi=+1 dan σ(→wT→xi)=0.1 , maka dalam verisimilitude sampel "pergi" 0.13. Jikayi=−1 dan σ(→wT→xi)=0.1 , maka dalam verisimilitude sampel "pergi" 1−0.1=0.94. Jikayi=−1 dan σ(→wT→xi)=0.9 , maka dalam verisimilitude sampel "pergi" 1−0.9=0.1Jelas, dalam kasus 1 dan 3, ketika probabilitas ditentukan dengan benar oleh algoritma, fungsi kemungkinan akan dimaksimalkan, itulah yang ingin kami dapatkan. Namun, pendekatan ini agak rumit, dan kami akan mempertimbangkan rekaman yang lebih ringkas di bawah ini. Tapi pertama-tama, logaritma fungsi kemungkinan dengan perubahan tanda, karena sekarang kita akan menguranginya.Llog(X,→y,→w)=n∑i=1(−[yi=+1]logeσ(→wT→xi)−[yi=−1]loge(1−σ(→wT→xi)))→min
Pengganti sebagai gantinya σ(→wT→xi) ekspresi 11+e−→wT→xi :
Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(1−11+e−→wT→xi))→min
Sederhanakan istilah yang tepat di bawah logaritma menggunakan teknik aritmatika sederhana dan dapatkan:Llog(X,→y,→w)=n∑i=1(−[yi=+1]loge(11+e−→wT→xi)−[yi=−1]loge(11+e→wT→xi))→min
Dan sekarang saatnya untuk menyingkirkan operator "jika ... maka ..." . Perhatikan bahwa saat objekyi milik kelas +1 , lalu dalam ekspresi di bawah logaritma, dalam penyebut, e diangkat ke kekuasaan −→wT→xi jika objek milik kelas −1 lalu $ e $ dinaikkan ke daya +→wT→xi .
Oleh karena itu, menulis gelar dapat disederhanakan dengan menggabungkan kedua kasus menjadi satu: −yi→wT→xi .
Kemudian fungsi kesalahan logistik berbentuk:Llog(X,→y,→w)=n∑i=1−loge(11+e−yi→wT→xi)→min
Sesuai dengan aturan logaritma, balikkan fraksi dan keluarkan tanda " − "(minus) per logaritma, kami mendapatkan:Llog(X,→y,→w)=n∑i=1loge(1+e−yi→wT→xi)→min
Berikut adalah fungsi kerugian Logistik kerugian , yang digunakan dalam set pelatihan dengan objek yang terkait dengan kelas:+1 dan −1 .
Nah, pada titik ini saya mengambil cuti saya dan kami mengakhiri artikel.← Karya penulis sebelumnya - "Kami membawa persamaan regresi linier ke dalam bentuk matriks"Bahan pendukung
1. Sastra
1) Analisis regresi terapan / N. Draper, G. Smith - edisi ke-2. - M .: Keuangan dan Statistik, 1986 (diterjemahkan dari bahasa Inggris)2) Teori Probabilitas dan Statistik Matematika / V.E. Gmurman - edisi ke-9. - M .: Sekolah Tinggi, 20033) Teori Probabilitas / N.I. Chernova - Novosibirsk: Novosibirsk State University, 20074) Analisis bisnis: dari data hingga pengetahuan / Paklin N. B., Oreshkov V. I. - edisi ke-2. - St. Petersburg: Peter, 20135) Ilmu Data Ilmu Data dari awal / Joel Grass - St. Petersburg: BHV Petersburg, 20176) Statistik praktis untuk spesialis Ilmu Data / P. Bruce, E. Bruce - St. Petersburg: BHV Petersburg, 20182. Kuliah, kursus (video)
1) Inti dari metode kemungkinan maksimum, Boris Demeshev2) Metode kemungkinan maksimum dalam kasus kontinu, Boris Demeshev3) Regresi logistik. Kursus terbuka ODS, Yury Kashnitsky4) Kuliah 4, Evgeny Sokolov (dengan video 47 menit)5) Regresi logistik, Vyacheslav Vorontsov3. Sumber internet
1) Model linier klasifikasi dan regresi2) Mudah untuk memahami regresi logistik3) Fungsi logistik kesalahan4) Tes independen dan rumus Bernoulli5) Balada IMF6) Metode kemungkinan maksimum7) Rumus dan sifat logaritma8) Mengapa jumlahnya e ?9) Klasifikasi linier