Menjelang awal kursus “Matematika untuk Ilmu Data. Advanced Course " kami melakukan webinar terbuka dengan topik" Metode Analisis Regresi dalam Ilmu Data ". Di sana kami berkenalan dengan konsep regresi linier, mempelajari di mana dan bagaimana mereka dapat diterapkan dalam praktik, dan juga mempelajari topik dan bagian analisis matematika, aljabar linier, dan teori probabilitas apa yang digunakan dalam bidang ini. Dosen - Peter Lukyanchenko , dosen di Sekolah Tinggi Ekonomi, Kepala Proyek Teknologi.
Jika kita berbicara tentang matematika dalam konteks Ilmu Data, kita dapat memilih tiga masalah yang paling sering diselesaikan (walaupun tentu saja ada lebih banyak masalah):

Mari kita bicarakan tugas-tugas ini secara lebih rinci:
- Tugas analisis regresi atau mengidentifikasi dependensi (ketika kita memiliki serangkaian pengamatan tertentu). Pada grafik di atas, Anda dapat melihat bahwa ada variabel tertentu x dan variabel tertentu y, dan kami mengamati nilai y untuk x tertentu. Kami tahu titik-titik ini dan mengetahui koordinatnya, dan kami juga tahu bahwa x entah bagaimana memengaruhi y, yaitu, kedua variabel ini saling bergantung satu sama lain. Secara alami, kami ingin menghitung persamaan ketergantungan mereka - untuk ini kami menggunakan model regresi linear pasangan klasik , ketika diasumsikan bahwa ketergantungan mereka dapat digambarkan oleh garis lurus tertentu. Dengan demikian, maka koefisien garis lurus dipilih untuk meminimalkan kesalahan dalam deskripsi data. Dan hanya pada jenis kesalahan apa (metrik kualitas) yang akan dipilih, hasil aktual dari membangun regresi linier tergantung.
- Tugas lain dari analisis data adalah sistem rekomendasi . Ini adalah ketika kita mengatakan bahwa ada, misalnya, toko online, mereka memiliki set barang tertentu, dan seseorang melakukan pembelian. Berdasarkan informasi ini, dimungkinkan untuk memberikan deskripsi orang ini dalam ruang vektor, dan, setelah membangun ruang vektor ini, membangun ketergantungan matematis dari probabilitas orang ini akan membeli produk ini atau itu, dengan mengetahui pembelian sebelumnya. Dengan demikian, kita berbicara tentang klasifikasi, ketika kita mengklasifikasikan pembeli potensial berdasarkan prinsip-prinsip: "beli-tidak beli", "menarik-tidak menarik", dll. Ada berbagai pendekatan: berbasis pengguna dan berbasis barang.
- Area ketiga adalah visi komputer . Dalam perjalanan tugas ini, kami mencoba menentukan di mana objek yang menarik bagi kami berada. Ini sebenarnya adalah solusi untuk masalah meminimalkan kesalahan dengan memilih piksel tertentu yang membentuk gambar objek.
Dalam ketiga masalah, ada optimasi, minimisasi kesalahan, dan keberadaan satu atau model lain yang menggambarkan ketergantungan variabel. Pada saat yang sama, di dalam masing-masing terletak representasi data yang diuraikan menjadi deskripsi vektor. Dalam artikel kami, kami akan memberikan perhatian khusus pada bagian yang mempengaruhi
model regresi .
Kami telah menyebutkan bahwa ada satu set pasangan data tertentu: X dan Y. Kami tahu nilai apa yang Y ambil sehubungan dengan X. Jika X adalah waktu, maka kami mendapatkan model deret waktu di mana Y adalah, katakanlah, harga minyak dan pada saat yang sama, rubel terhadap nilai tukar dolar, dan X adalah periode waktu tertentu dari 2014 hingga 2018:
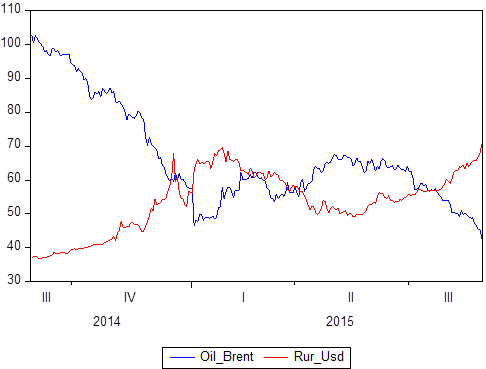
Jika Anda membangun secara grafis, jelas bahwa kedua seri waktu ini saling bergantung. Setelah mendefinisikan konsep korelasi, Anda dapat menghitung tingkat ketergantungannya, dan kemudian, jika Anda tahu bahwa beberapa nilai berkorelasi sempurna (korelasinya 1 atau -1), Anda dapat menggunakan ini untuk meramalkan tugas atau untuk tugas deskripsi.
Perhatikan ilustrasi berikut:
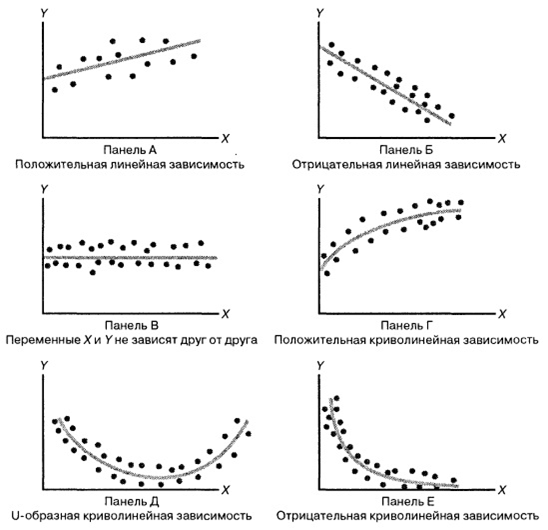
Bagian tersulit dalam pembentukan model regresi adalah
awalnya menempatkan beberapa fungsi spesifik dalam ingatannya . Misalnya, untuk Gambar A adalah Y = kX + b, untuk B adalah Y = -kX + b, dalam gambar C "permainan" sama dengan beberapa angka, grafik pada gambar D kemungkinan besar didasarkan pada root dari " X ", di dasar D, mungkin parabola, dan di dasar E - hiperbola.
Ternyata
kita memilih beberapa model ketergantungan data , dan jenis-jenis ketergantungan antara variabel acak berbeda. Semuanya tidak begitu jelas, karena bahkan dalam gambar sederhana ini kita melihat berbagai ketergantungan. Dengan memilih hubungan tertentu, kita dapat menggunakan metode regresi untuk mengkalibrasi model.
Kualitas perkiraan Anda akan tergantung pada model mana yang Anda pilih . Jika kita fokus pada model regresi linier, maka kita mengasumsikan bahwa ada serangkaian nilai nyata:

Angka ini menunjukkan 4 nilai yang diamati dari X1, X2, X2, X4. Untuk masing-masing X, nilai Y diketahui (dalam kasus kami, ini adalah poin: P1, P2, P3, P4). Inilah poin-poin yang sebenarnya kami amati pada data. Jadi, kami menerima dataset tertentu. Dan untuk beberapa alasan, kami memutuskan bahwa regresi linier paling menggambarkan hubungan antara X dan pemain. Selanjutnya, seluruh pertanyaan adalah bagaimana membangun persamaan garis lurus Y = b
1 + b
2 X, di mana b
2 adalah koefisien kemiringan, b
1 adalah koefisien persimpangan. Seluruh pertanyaan adalah b2 dan b1 mana
yang paling baik diatur sehingga garis lurus ini menggambarkan hubungan antara variabel-variabel ini seakurat mungkin.
Poin R
1 , R
2 , R
3 , R
4 adalah nilai yang diberikan model kami pada nilai X. Apa yang terjadi? Poin P adalah poin yang benar-benar kami amati (sebenarnya dikumpulkan), dan poin R adalah poin yang kami amati dalam model kami (yang dihasilkannya). Berikut ini adalah logika manusia yang sangat sederhana: sebuah
model akan dianggap kualitatif jika dan hanya jika titik R sedekat mungkin dengan titik P.Jika kita membangun jarak antara titik-titik ini untuk "X" yang sama (P
1 - R
1 , P
2 - R
2 , dll.), Maka kita mendapatkan apa yang disebut kesalahan regresi linier. Kami mendapatkan penyimpangan dalam regresi linier, dan penyimpangan ini disebut U
1 , U
2 , U
3 ... U
n . Dan kesalahan ini bisa dalam plus atau minus (kita bisa melebih-lebihkan atau meremehkan). Untuk membandingkan penyimpangan ini, mereka perlu dianalisis. Metode yang sangat besar dan indah digunakan di sini - mengkuadratkan (mengkuadratkan “membunuh” tanda). Dan jumlah kuadrat dari semua penyimpangan dalam statistik matematika disebut RSS (Jumlah Sisa Kuadrat). Dengan meminimalkan RSS dengan b
1 dan dengan meminimalkan RSS dengan b
2 , kami memperoleh koefisien optimal yang sebenarnya diturunkan
dengan metode kuadrat terkecil .
Setelah kami membangun regresi, menentukan koefisien optimal b
1 dan b
2 , dan kami memiliki persamaan regresi, masalah tidak berakhir di sana, dan masalah terus berkembang. Faktanya adalah jika regresi itu sendiri ditandai pada satu grafik, semua nilai yang kita miliki, serta nilai rata-rata "permainan", maka jumlah kesalahan kuadrat dapat diklarifikasi.
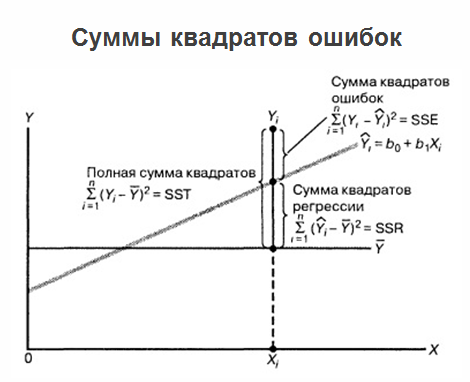
Pada saat yang sama, dianggap berguna untuk menampilkan kesalahan prediksi regresi sehubungan dengan variabel X. Lihat gambar di bawah ini:

Kami mendapat semacam regresi dan menggambar data sebenarnya. Kami mendapat jarak dari setiap nilai riil ke regresi. Dan kami menggambarnya relatif terhadap nilai nol untuk nilai yang sesuai dari X. Dan pada gambar di atas kita melihat gambar yang sangat buruk:
kesalahan tergantung pada X. Beberapa ketergantungan korelasi dengan jelas dinyatakan:
semakin jauh sepanjang "X" kita bergerak, semakin besar signifikansi kesalahan . Ini sangat buruk. Kehadiran korelasi dalam kasus ini menunjukkan bahwa kami keliru mengambil model regresi, dan ada beberapa parameter yang kami "tidak pikirkan" atau hanya diabaikan. Lagi pula, jika semua variabel ditempatkan di dalam model, kesalahan harus benar-benar acak dan tidak harus bergantung pada apa faktor Anda sama.
Kesalahan harus dengan distribusi probabilitas yang sama , jika tidak, prediksi Anda akan salah. Jika Anda telah menggambar kesalahan model Anda di pesawat dan bertemu dengan segitiga yang berbeda, lebih baik untuk memulai semua dari awal dan sepenuhnya menceritakan kembali model tersebut.
Dengan menganalisis kesalahan, Anda bahkan dapat segera memahami di mana kesalahan perhitungannya, jenis kesalahan apa yang mereka buat. Dan di sini kita tidak bisa gagal menyebutkan teorema Gauss-Markov:

Teorema menentukan kondisi di mana estimasi yang diperoleh dengan metode kuadrat terkecil adalah yang terbaik, konsisten, efektif dalam kelas estimasi linier yang tidak bias.
Kesimpulannya dapat ditarik sebagai berikut: sekarang kita memahami bahwa
area membangun model regresi, dalam arti tertentu, adalah puncak dari sudut pandang matematika , karena menggabungkan semua bagian yang mungkin sekaligus, yang dapat berguna dalam analisis data, misalnya:
- aljabar linier dengan metode representasi data;
- analisis matematis dengan teori optimisasi dan sarana analisis fungsi;
- teori probabilitas dengan cara menggambarkan peristiwa dan jumlah acak dan memodelkan hubungan antar variabel.
Kolega, saya sarankan semua sama, tidak terbatas pada membaca dan menonton seluruh webinar . Artikel itu tidak termasuk momen yang berkaitan dengan pemrograman linier, optimisasi dalam model regresi, dan detail lain yang mungkin berguna bagi Anda.