Ask Ethan # 4: Mapas Astronômicos Estranhos

Eu tenho um mapa existencial, cuja superfície inteira diz "Você está aqui".
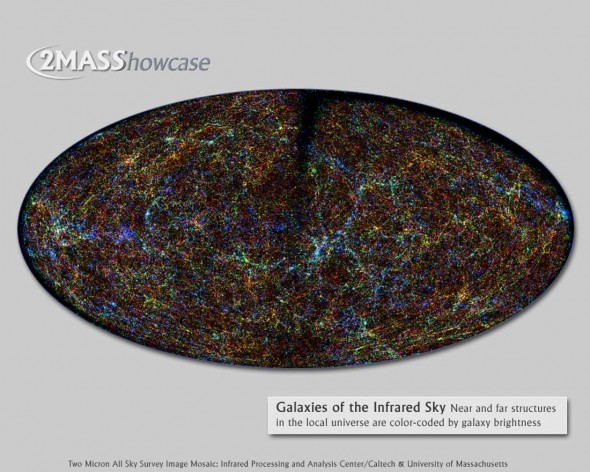
Steven Wright

Reader pergunta:

Os mapas cósmicos de radiação de fundo de microondas parecem um oval plano. Como isso se relaciona com a visão do céu, que é uma esfera? Por exemplo, um mapa da Terra pode ser distorcido para nos mostrar o mundo em duas dimensões ou ser cortado em fatias. Que parte do céu estamos olhando enquanto observamos o mapa KMFI? Ela está distorcida? E se isso é apenas parte do céu - falta alguma informação importante?

Ele fala sobre essas fotos: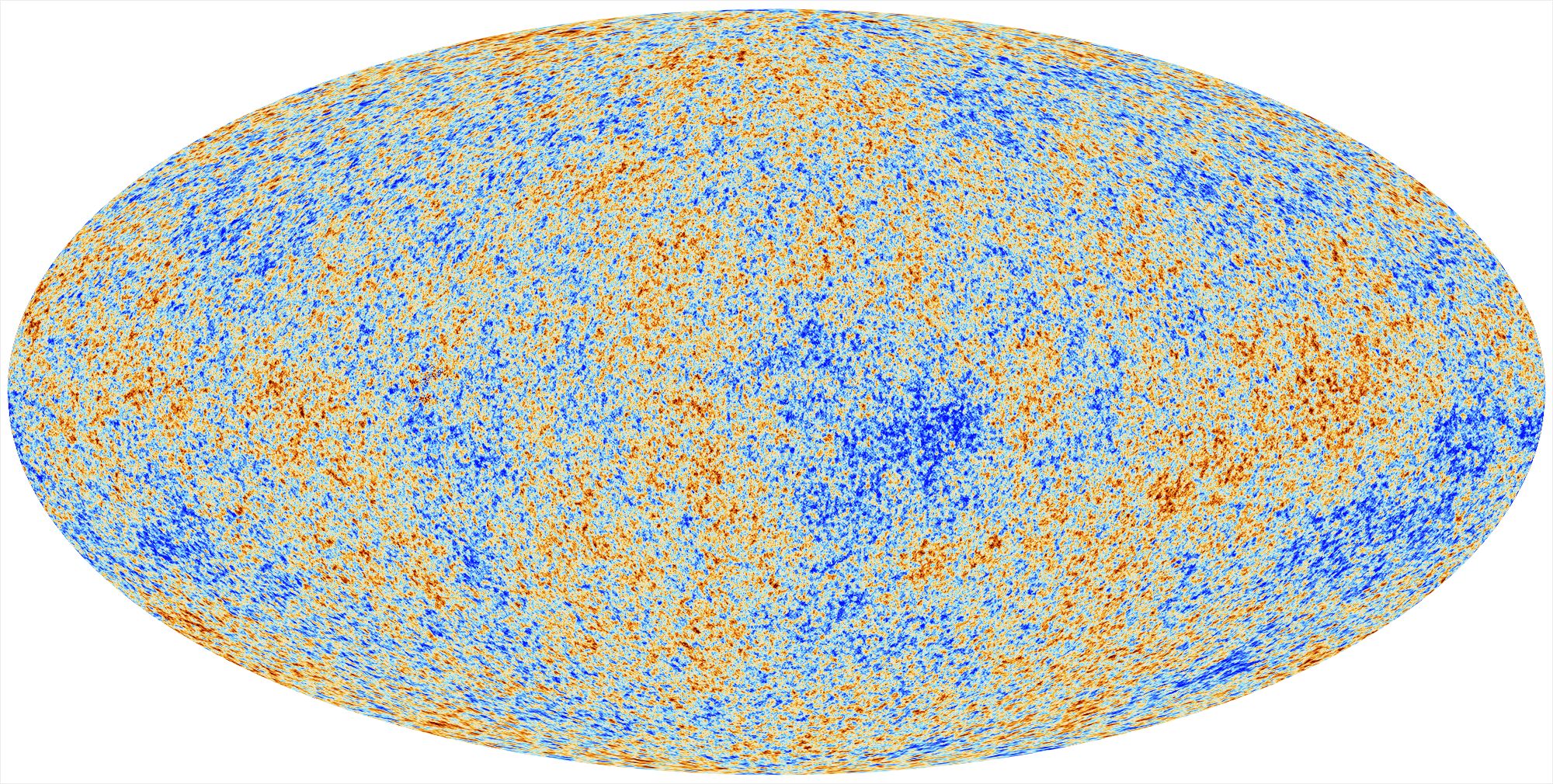


é difícil de acreditar, mas o céu inteiro está realmente criptografado aqui.

Imagine a Terra:


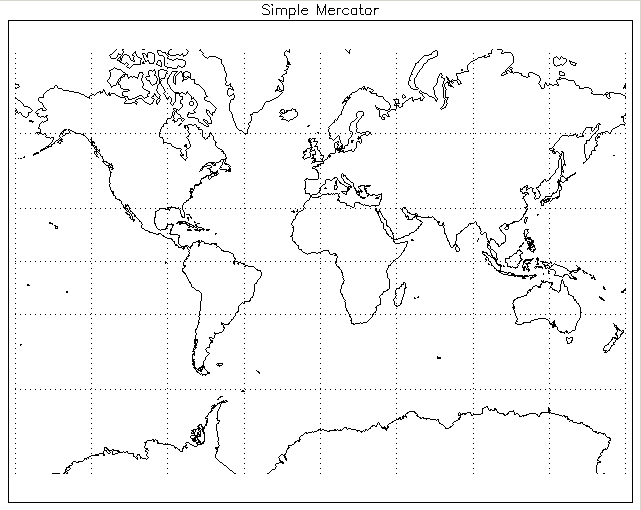você está acostumado a essas cartas. Se você mora nos EUA, está acostumado ao fato de que a América do Norte geralmente está localizada no centro do mapa. Se estiver no Reino Unido, estamos acostumados ao fato de o cartão estar centrado para que a França seja cortada dos dois lados.

Esses cartões são geralmente aceitos e, ao mesmo tempo, extremamente imprecisos. Você ficará surpreso que a África tenha mais do que o dobro do tamanho da Antártica, a América do Sul seja mais que a Rússia e a Austrália seja três vezes maior que a Groenlândia. Tudo isso se deve ao fato de a superfície da Terra não ser plana, mas localizada em uma esfera.



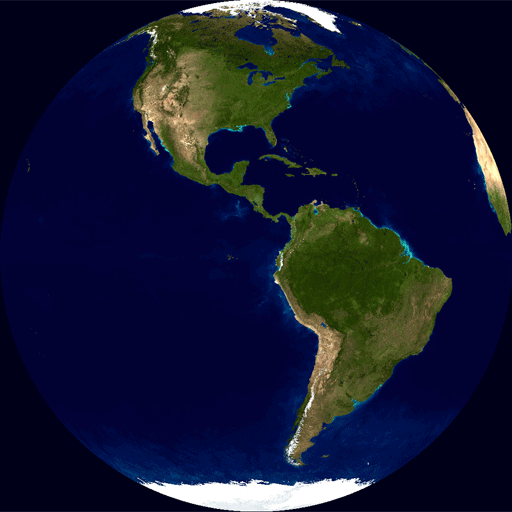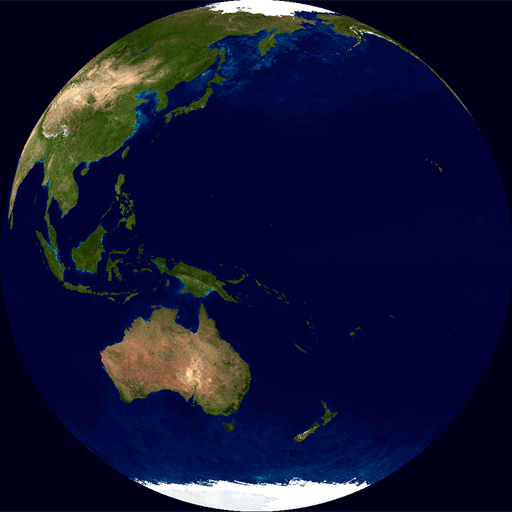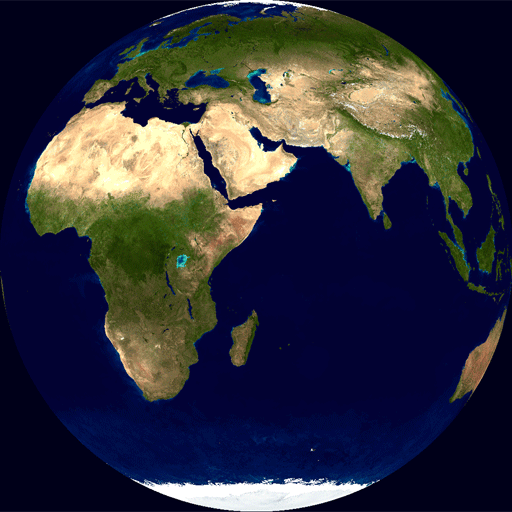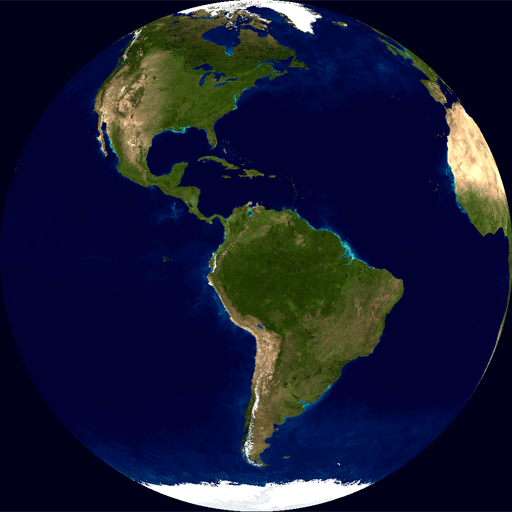Se você tentar expandir a superfície de uma esfera, nada de bom resultará dela. Pegue uma laranja, descasque-a e tente endireitar a pele sobre a mesa. Na melhor das hipóteses, você terminará com algo assim:



Ao espalhar uma esfera em um avião, você precisa sacrificar alguma coisa. Se você insistir em criar um mapa plano, poderá fazer um mapa conectado por perpendiculares à latitude e longitude, mas será impreciso. Isso é chamado de projeção de Mercator.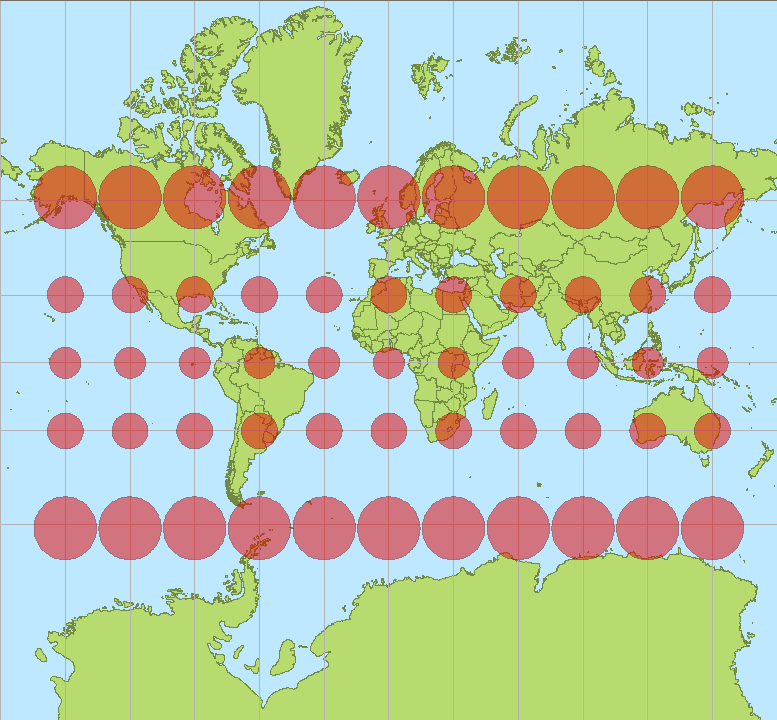


Distorções de áreas na projeção Mercator

Você pode manter a precisão da apresentação e a perpendicularidade da latitude e longitude, se negligenciar as partes conectadas do mapa - como no exemplo da casca de laranja.

Um compromisso pode ser alcançado pressionando a longitude e aumentando a latitude:



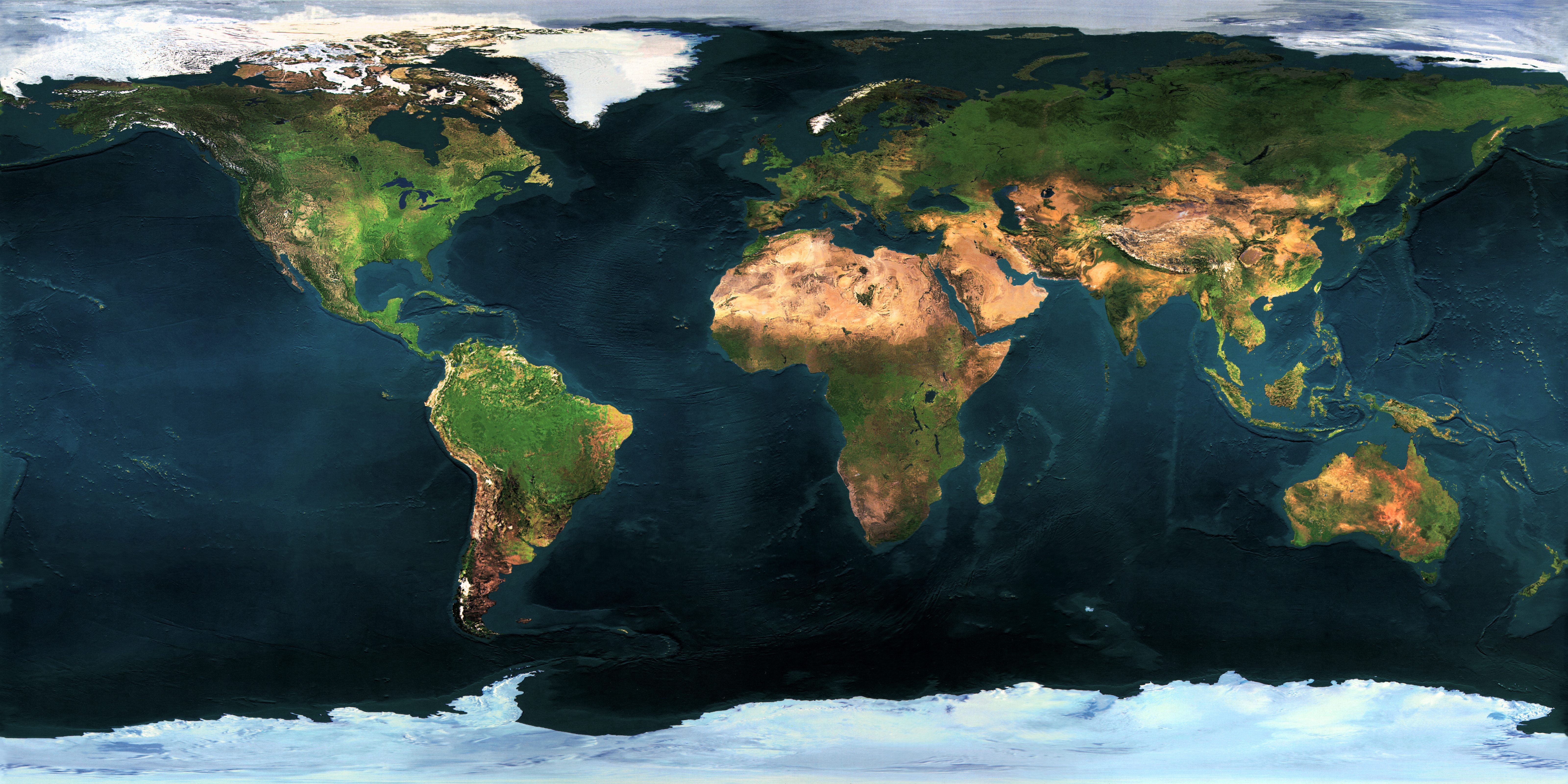tudo isso é bastante inconveniente, mas é mais conveniente não fazê-lo. É impossível preservar a perpendicularidade da latitude e longitude, a precisão da apresentação e a conexão do mapa - a superfície da esfera não pode ser perfeitamente endireitada.

Isso vale para um mapa da Terra e para um mapa do céu.



O que quer que façamos ao renderizar o céu, teremos que sacrificar alguma coisa. A única questão é o que exatamente.

Como o tamanho é importante na astronomia, não podemos sacrificar isso. Também é importante manter a coerência da imagem - não há lacunas no espaço. Resta negligenciar a perpendicularidade da latitude e longitude (declinação e ascensão reta, como são chamadas em astronomia), para que ângulos e formas não sejam representados com precisão. Isso pode ser feito com o mapa da Terra: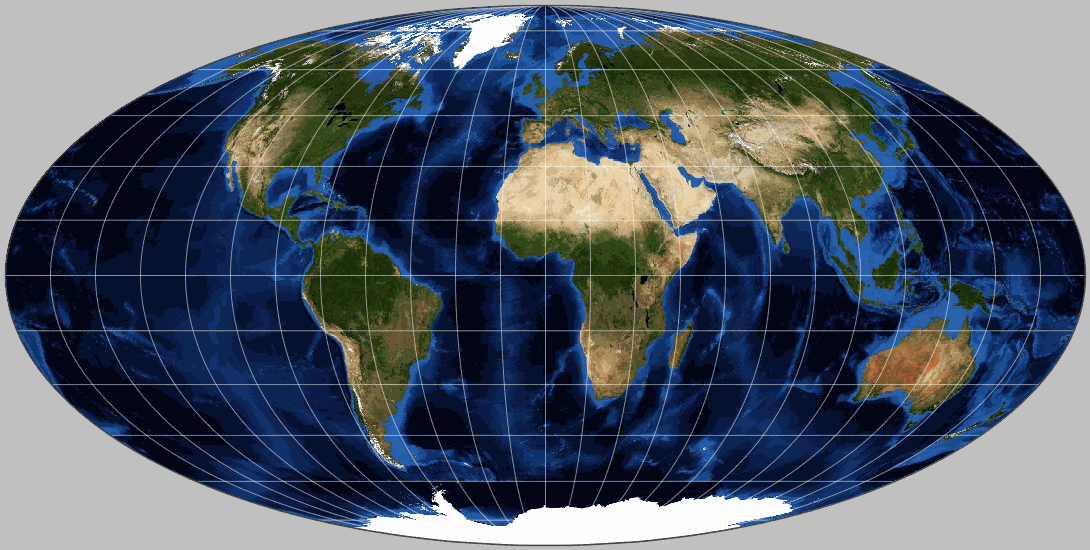



esse método é chamado de projeção de Mullveide e, se você se lembra do que eu falei anteriormente:

• África mais que dobra a Antártica
• A América do Sul é mais do que a Rússia
• A Austrália é três vezes maior que a Groenlândia

será mais fácil acreditar quando se olha para uma projeção dessas. É o que fazemos com o céu - usamos essa projeção para uma representação bidimensional.

Em vez de mostrar uma fotografia de uma parte do céu:



mostramos tudo de uma vez na projeção galáctica de Mollweide:



O telescópio Planck olhou para a parte de microondas do espectro e viu toda a radiação de todas as fontes no céu, incluindo galáxias, luz e poeira zodiacais, bem como pré-históricas reflexão cósmica do Big Bang.



E, finalmente, subtraindo a luz galáctica, a temperatura média do corpo negro de 2.725 K



KMPI e nosso movimento pelo universo,


podemos ver uma parte importante da radiação residual do KMPF.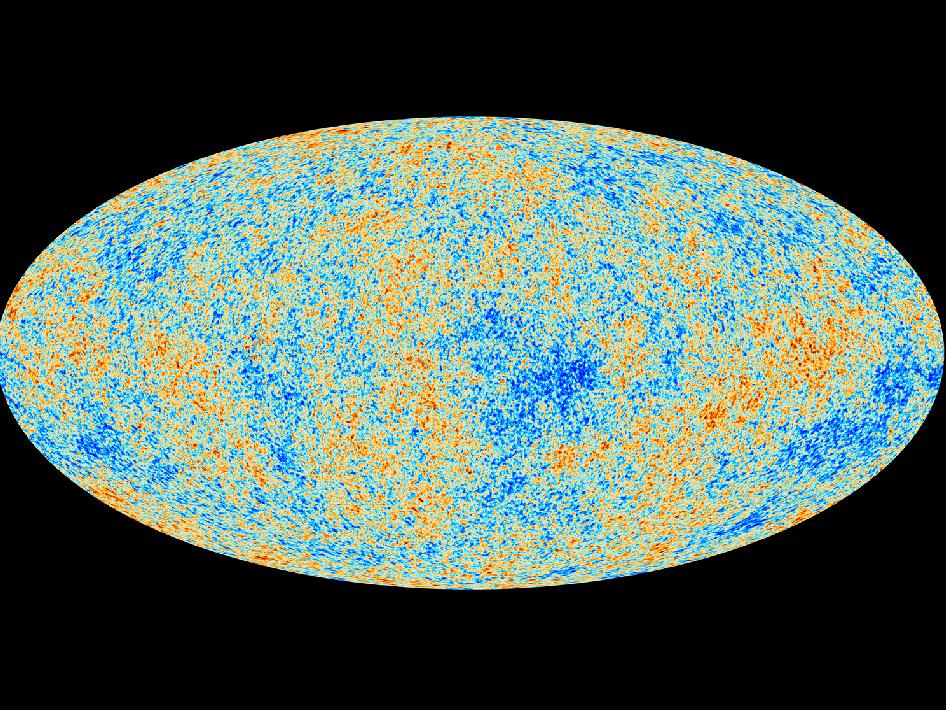


Nós a dividimos em componentes usando harmônicos esféricos, analisamos e percebemos o universo. Tudo isso é feito na projeção de Mollveide e, portanto, os mapas celestes são assim. Nada está faltando neles - você pode ver o céu inteiro de cada vez. Você só precisa se acostumar um pouco.

Source: https://habr.com/ru/post/pt380791/