O "paradoxo da inspeção" está em toda parte

Muitas pessoas conhecem o chamado "paradoxo da amizade" nas redes sociais, mencionado pela primeira vez no trabalho científico de 1991, quando as redes sociais estavam apenas offline. Esse paradoxo se aplica às redes sociais modernas na Internet.

Se você pegar qualquer usuário do Facebook e selecionar aleatoriamente algum de seus amigos, com uma probabilidade de 80%, um amigo terá mais "amigos". As pessoas que são novas na estatística matemática estão muito chateadas pelo fato de quase todos os amigos terem mais sucesso na comunicação do que eles mesmos. Mas não há razão para a depressão: deve ser assim, de acordo com a ciência e o senso comum.

O Paradoxo da Amizade é uma das formas do “Paradoxo da Inspeção”, que é encontrado em toda parte e muitas vezes engana os habitantes da cidade.

A essência do paradoxo da amizade é que os usuários com um grande número de amigos têm maior probabilidade de pertencer à amostra estatística. Por exemplo, de acordo com a Stanford Large Network Dataset Collection , o usuário médio do Facebook tem 42 amigos em uma amostra de 4.000 pessoas, e cada um desses amigos tem uma média de 91 amigos.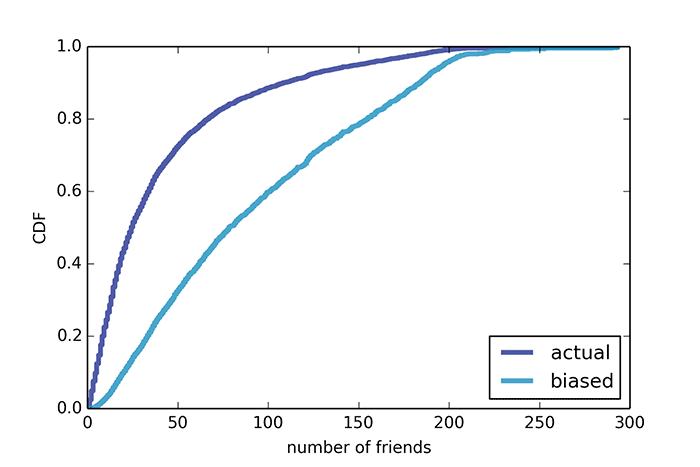



O mesmo é observado em outras áreas de pesquisa.

Por exemplo, o paradoxo do tamanho da classe. Suponha que entrevistemos os alunos quantas pessoas estudam com eles em um grupo e, em seguida, derivemos a média aritmética de suas respostas - e obtemos 56 pessoas. Mas a administração da universidade diz que o número médio de estudantes em um grupo é 31. Curiosamente, ninguém está mentindo, e os dois valores são justos. Apenas durante a pesquisa, estudantes de grandes grupos têm maior probabilidade de entrar na amostra, porque na verdade existem mais deles. Se tivermos dois grupos de 10 e 100 pessoas, 100 de 110 participantes nomearão o tamanho do grupo como 100 pessoas, e apenas 10 pessoas nomearão o tamanho do grupo 10. O tamanho médio do grupo, de acordo com esta pesquisa, será de 92 alunos.

Parece um erro comum, mas é uma fonte de mal-entendidos em muitas situações reais. Por exemplo, ao analisar o tráfego de passageiros em transporte público. Um professor de ciência da computação, Allen Downey, para um artigo no Journal of the American Statistical Society fornece um exemplo do tempo médio entre os trens da Red Line em Boston. Ele registrou a hora de chegada de 70 trens entre as 17:00 e as 18:00.



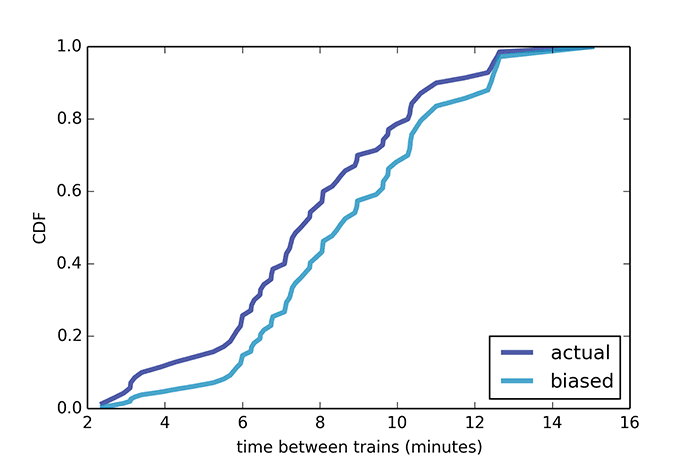O intervalo mínimo entre os trens foi de 3 minutos, o máximo - 15 minutos. De acordo com dados reais, o intervalo médio entre trens é de 7,8 minutos, ou seja, o tempo médio de espera de um trem deve ser de aproximadamente 3,9 minutos. Mas uma pesquisa de passageiros mostra que o tempo médio de espera foi de 4,4 minutos e o intervalo entre trens foi de 8,8 minutos, ou seja, 15% a mais.

O motivo é que, com um atraso maior no trem, mais passageiros o aguardam, enquanto os trens que chegam com um intervalo mais curto ficam menos lotados. Consequentemente, a maioria dos passageiros reclama da queda do carro e do longo tempo de espera do trem, enquanto, segundo a empresa, o tempo e a carga médios dos carros são normais.

O mesmo problema com voos. A maioria dos passageiros fala sobre salas de espera cheias de cabine, enquanto as companhias aéreas reclamam de perder lucros porque muitos voos voam quase vazios. Ambos estão certos.

O “paradoxo da inspeção” é observado, por exemplo, em corridas de longa distância ou quando se viaja de carro pela rodovia. Em cada um desses casos, o participante do movimento ultrapassa "muito devagar" e é ultrapassado por "muito rápido". Isso cria uma impressão subjetiva de que todos os participantes do movimento são divididos em muito devagar ou muito rápido, mas não na média.

O exemplo mais recente de Allen Downey nasceu depois de ler Orange - The Hit of the Season, um livro de memórias de Piper Kerman, que passou 13 meses na prisão federal. Em um dos fragmentos do livro, ela expressa surpresa pela longa duração das sentenças que os prisioneiros estão cumprindo. Obviamente, a garota não está familiarizada com as leis da estatística matemática. Mas, de acordo com o paradoxo da inspeção, se você for preso em um momento aleatório e escolher um prisioneiro aleatório, então com um alto grau de probabilidade, ele será condenado a um longo período de prisão. Isso não é evidência do sistema penitenciário desumano dos Estados Unidos, mas uma simples conclusão do paradoxo da inspeção.



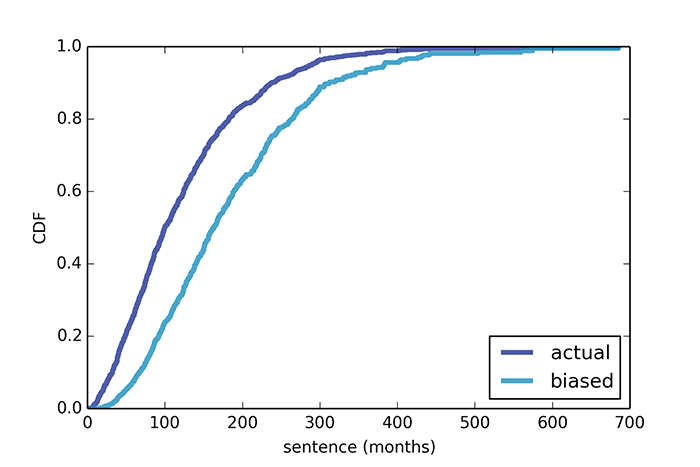Segundo dados oficiais da Comissão de Penas dos EUA, o prazo médio é de 121 meses, e o "prazo médio subjetivo" para entrevistar prisioneiros é de 183 meses.

Mesmo ao entrevistar prisioneiros próximos por treze meses, como mostra o cálculo, o resultado médio obtido não difere muito da pesquisa inicial única.



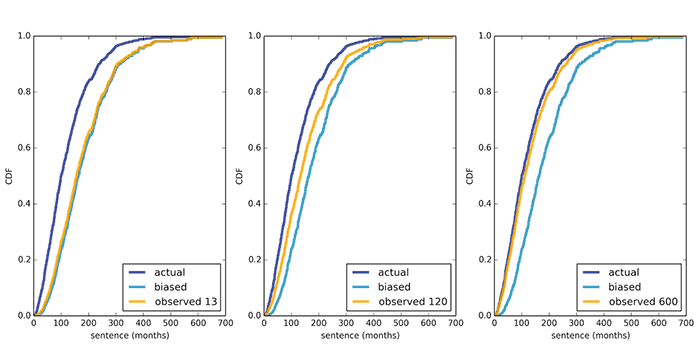Um número mais ou menos objetivo pode ser obtido entrevistando-se por 600 meses ou mais.

Source: https://habr.com/ru/post/pt383787/