Alguns sensores de aceleração requerem calibração zero adicional após a montagem na placa. Quando vi várias fontes com a calibração de sensores de aceleração, onde o componente G era levado em consideração simplesmente subtraindo = 9,8 m / s2 do eixo Z, surgiu a idéia de escrever esta nota.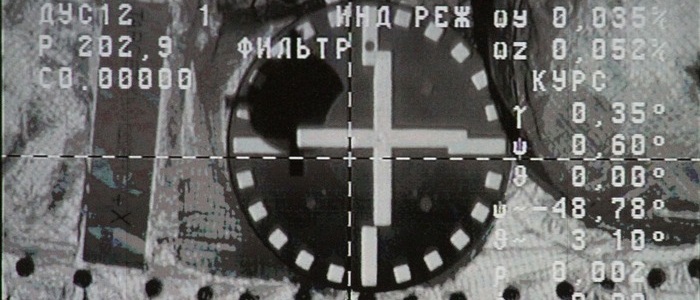
Estrutura de publicação
- Problema
- Declaração do problema e método de solução
- Como conseguir os pontos?
- Como calcular o centro da bola?
- Como acelerar a busca pelo centro da bola?
- De que outra forma acelerar a busca pelo centro da bola?
- Sobre erros de medição
- Total
Problema
Qual é o problema - os sensores MEMS após a instalação na placa sofrem pequenas deformações que afetam:- posição zero;
- escala de valores medidos;
- a perpendicularidade dos eixos entre si.
E se a escala e a perpendicularidade forem violadas de maneira não tão perceptível, a posição do zero ficará emaranhada tangivelmente. Por exemplo, se você converter o valor típico do deslocamento zero para o acelerômetro do sensor MPU9250 em m / s 2 , isso será obtido na região de 0,2 m / s 2 . Ou seja, o sensor está parado, mas mostra aceleração e, após 5 segundos, obtemos uma velocidade de 1 m / s. Por um lado, todos os dados do sensor são sempre passados por algum tipo de filtro (por exemplo, tal ). Mas, por outro lado, por que o filtro deve compensar constantemente esse viés? Afinal, o sensor mostrará movimento onde não está. Isso reduz a precisão do resultado. Em suma, você precisa encontrar o valor de correção uma vez e subtrair esse valor de suas leituras durante a operação do sensor.A solução mais simples para encontrar o valor do deslocamento zero, que vem à mente imediatamente, é criar as condições sob as quais o sensor deve mostrar com precisão zero. O valor registrado no sensor é o valor do deslocamento zero! Assim? Mas a gravidade não está constantemente atuando no acelerômetro. Para evitá-lo, será necessária a ausência de peso (o lançamento não funcionará). O campo magnético da Terra atua na bússola e sua rotação no giroscópio. Portanto, se você não tem uma espaçonave pessoal, precisará criar algo.A segunda solução que vem à mente imediatamente é colocar o sensor (ou melhor, seu eixo) em uma posição em que saberemos exatamente o que o sensor deve mostrar. A diferença entre o que o sensor mostra e o que deve mostrar - e haverá um deslocamento zero! Assim? Por exemplo, sabemos que se o acelerômetro for colocado em um nível com o horizonte, em teoria, o vetor de aceleração gravitacional será direcionado exatamente ao longo do eixo Z do sensor. A magnitude do vetor de aceleração que conhecemos.No entanto, há um problema. Consiste no fato de que não podemos definir com precisão o eixo do sensor em um nível com o horizonte. O fato é que a superfície na qual confiaremos não é paralela à placa de circuito impresso. Isso, por sua vez, não é paralelo ao local em que o sensor está localizado. O sensor em si não fica exatamente no seu local e os eixos dentro do sensor não são paralelos ao corpo do sensor. O erro ao definir o eixo em relação ao horizonte em 1 grau fornece uma projeção comparável em tamanho ao valor do deslocamento do zero, que queremos encontrar. No caso de um magnetômetro, também não sabemos para onde o vetor do campo magnético é direcionado. Em teoria, ao norte. Mas, na prática, o próprio campo magnético da Terra é heterogêneo em intensidade e direção. Além disso, objetos de metal próximos fazem seus ajustes.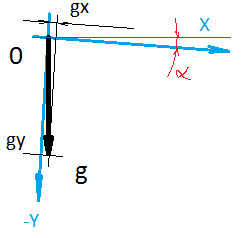
Declaração do problema e método de solução
A tarefa é a seguinte: precisamos determinar o vetor de deslocamento zero usando as leituras do sensor, que sempre registram o vetor de deslocamento + vetor de influência externa constante (aceleração gravitacional, rotação da Terra, campo magnético da Terra), a magnitude e a direção que não sabemos (no caso do acelerômetro) sabemos o valor, mas, novamente, a escala do sensor pode não ser igual a 1).Maneira de resolver. Este artigo propõe determinar o vetor de deslocamento da seguinte maneira. Pegamos e giramos o sensor de todas as maneiras e registramos as leituras do sensor. Após N medições, os valores retirados do sensor e localizados no gráfico serão uma bola, cujo raio é a magnitude do impacto externo e o centro é o deslocamento zero exato desejado.Como conseguir os pontos?
Para facilitar o próprio procedimento de medição, você pode escrever um programa simples. Ele deve registrar os sensores quando o dispositivo estiver parado. Só precisamos colocar o dispositivo na posição desejada. Para determinar um estado estacionário, também é adequado um acelerômetro não calibrado - basta fazer a diferença entre o valor atual e o anterior. E se houver mais barulho, então corrigimos o movimento. Meu limite é obtido na região de 0,07G. Se você segurar com as mãos, mais do que esse valor sairá. Usei fita adesiva para fixar a posição. Se ainda não der certo, verifique se há uma geladeira, um ventilador ou algo semelhante por perto.Como pode estar no código
static TSumSensorsData g_sens_data[2];
static int32_t g_sens_data_sum_cnt[2];
static uint8_t g_sens_data_num;
IS_INTERRUPT void on_dma_raw_ready_calibrate_step1()
{
SensorRawBuffer *raw = sensor_get_raw_buffer();
g_sens_data[g_sens_data_num].acc_x += swap_i16(raw->accell_x_unswap);
g_sens_data[g_sens_data_num].acc_y += swap_i16(raw->accell_y_unswap);
g_sens_data[g_sens_data_num].acc_z += swap_i16(raw->accell_z_unswap);
g_sens_data[g_sens_data_num].gyro_x += swap_i16(raw->gyro_x_unswap);
g_sens_data[g_sens_data_num].gyro_y += swap_i16(raw->gyro_y_unswap);
g_sens_data[g_sens_data_num].gyro_z += swap_i16(raw->gyro_z_unswap);
g_sens_data[g_sens_data_num].mag_x += raw->mag_x_raw * g_mag_calibrate.kx;
g_sens_data[g_sens_data_num].mag_y += raw->mag_y_raw * g_mag_calibrate.ky;
g_sens_data[g_sens_data_num].mag_z += raw->mag_z_raw * g_mag_calibrate.kz;
g_sens_data_sum_cnt[g_sens_data_num]++;
}
void sensors_calibrate_program(FlashROM *flash_ptr)
{
double calibrate_result_error[3];
TVector16 calibrate_result[3];
int32_t radius[ACCEL_NO_MOTION_DETECT_COUNT];
uint8_t raw_is_deleted[ACCEL_NO_MOTION_DETECT_COUNT];
TVector16 raw[3][ACCEL_NO_MOTION_DETECT_COUNT];
. . .
g_sens_data_sum_cnt[0] = 0;
g_sens_data_num = 0;
int16_t prev_avg_x = 0;
int16_t prev_avg_y = 0;
int16_t prev_avg_z = 0;
int8_t low_motion_cnt = 0;
while(low_motion_cnt < ACCEL_NO_MOTION_DETECT_COUNT)
{
if (g_sens_data_sum_cnt[g_sens_data_num] >= ACCEL_NO_MOTION_DETECT_SAMPLES)
{
uint8_t new_data_num = (g_sens_data_num + 1) & 1;
g_sens_data[new_data_num].acc_x = 0;
g_sens_data[new_data_num].acc_y = 0;
g_sens_data[new_data_num].acc_z = 0;
g_sens_data[new_data_num].gyro_x = 0;
g_sens_data[new_data_num].gyro_y = 0;
g_sens_data[new_data_num].gyro_z = 0;
g_sens_data[new_data_num].mag_x = 0;
g_sens_data[new_data_num].mag_y = 0;
g_sens_data[new_data_num].mag_z = 0;
g_sens_data_sum_cnt[new_data_num] = 0;
uint8_t old_data_num = g_sens_data_num;
g_sens_data_num = new_data_num;
int16_t avg_x = g_sens_data[old_data_num].acc_x / g_sens_data_sum_cnt[old_data_num];
int16_t avg_y = g_sens_data[old_data_num].acc_y / g_sens_data_sum_cnt[old_data_num];
int16_t avg_z = g_sens_data[old_data_num].acc_z / g_sens_data_sum_cnt[old_data_num];
int16_t dx = avg_x - prev_avg_x;
int16_t dy = avg_y - prev_avg_y;
int16_t dz = avg_z - prev_avg_z;
prev_avg_x = avg_x;
prev_avg_y = avg_y;
prev_avg_z = avg_z;
if ((abs_i16(dx) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dy) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dz) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE))
{
raw[RAW_ACC][low_motion_cnt].x = avg_x;
raw[RAW_ACC][low_motion_cnt].y = avg_y;
raw[RAW_ACC][low_motion_cnt].z = avg_z;
raw[RAW_GYRO][low_motion_cnt].x = g_sens_data[old_data_num].gyro_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].y = g_sens_data[old_data_num].gyro_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].z = g_sens_data[old_data_num].gyro_z / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].x = g_sens_data[old_data_num].mag_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].y = g_sens_data[old_data_num].mag_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].z = g_sens_data[old_data_num].mag_z / g_sens_data_sum_cnt[old_data_num];
low_motion_cnt++;
beep();
delay_ms(2000);
}
}
}
. . .
}
Para colocar a bola no gráfico, você precisa torcer o dispositivo com o sensor de acordo com um determinado esquema. Para esses fins, o globo é adequado, pois possui uma marcação. Você pode pensar que precisa esculpir em todo o mundo. Mas isso não é verdade.Exemplo de resultado incorreto É necessário esculpir o sensor não em toda a superfície do globo, mas em um meridiano. Suponha que levemos sete pontos no meridiano (o primeiro e o último nos polos norte e sul). Em cada ponto do meridiano, conectamos o dispositivo ao globo e ainda giramos o dispositivo em torno de seu eixo com um certo passo, por exemplo, 30 a 35 graus. Acontece que, se você girar 12 vezes em torno de seu eixo, serão obtidos 7 pontos no total de 84 medições.
A beleza do método é que tudo pode ser feito "no joelho". A precisão do posicionamento não desempenha um papel especial, basta girar de acordo com o esquema para que o vetor de influência externa no gráfico atraia uma bola. O correto se parece com isso - veja a figura (o centro está marcado com uma marca).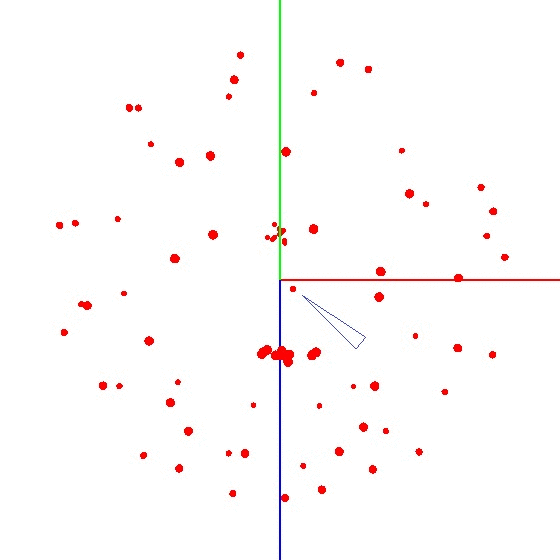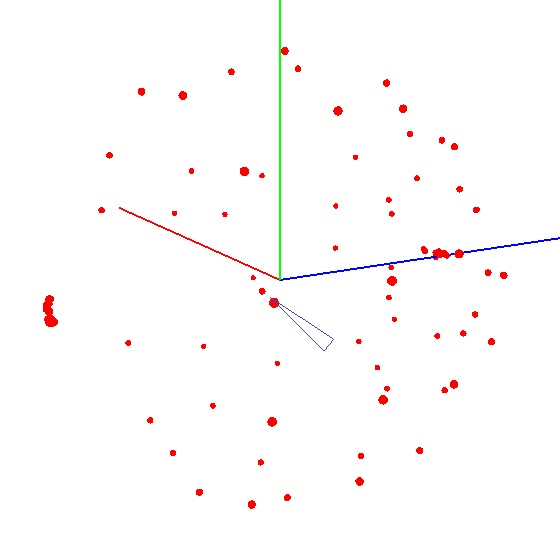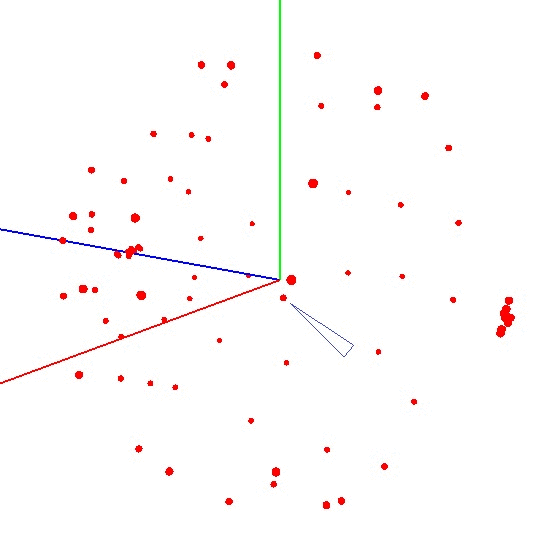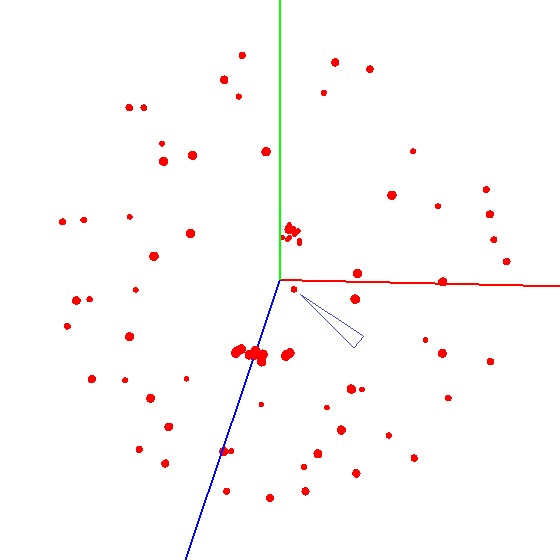
Como calcular o centro da bola?
Esta é uma tarefa interessante e possui várias soluções. Pode parecer que, para procurar o centro, basta tomar a média aritmética das coordenadas dos pontos obtidos. No entanto, não é assim - os pontos podem ser localizados de maneira desigual na bola (veja a Fig.).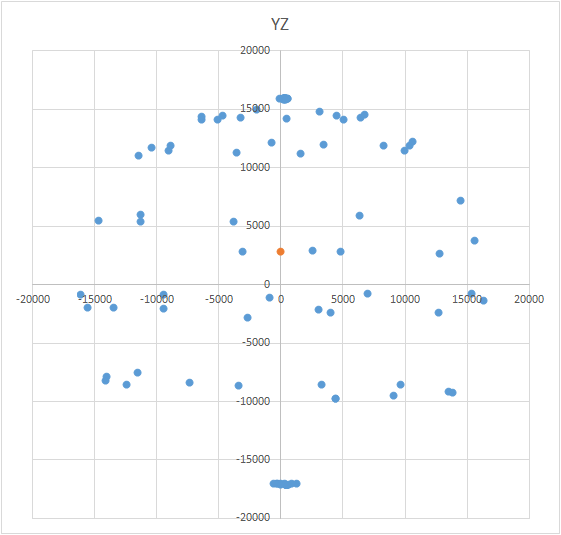
A equação da aparência de esferas como a seguinte: (x - a) 2 + (Y - B) 2 + (z - C) 2 = R 2 , em que X, Y, Z são as coordenadas do ponto encontra-se sobre a bola. A, B, C são as coordenadas do centro nos eixos x, ye z, respectivamente. R é o raio da bola. Você pode criar um sistema de equações e tentar resolvê-lo mais simplesmente usando algum método. Ou você pode simplesmente encontrar o centro (é como um método de aproximações sucessivas). O significado do método é simples: o valor do erro (X - A) 2 + (Y - B) 2+ (Z - C) 2 - R 2 deve tender para zero. Isso significa que a soma dessas quantidades para todos os pontos da esfera também deve tender a zero. Sabendo disso, podemos escolher os valores A, B e C para os quais o erro para todos os pontos será mínimo. A área de pesquisa é limitada pelo tamanho da bola (cubo condicional). Ou seja, devemos colocar sequencialmente o centro da bola em todos os pontos do cubo e calcular o erro. Onde há um erro mínimo - existe o centro.
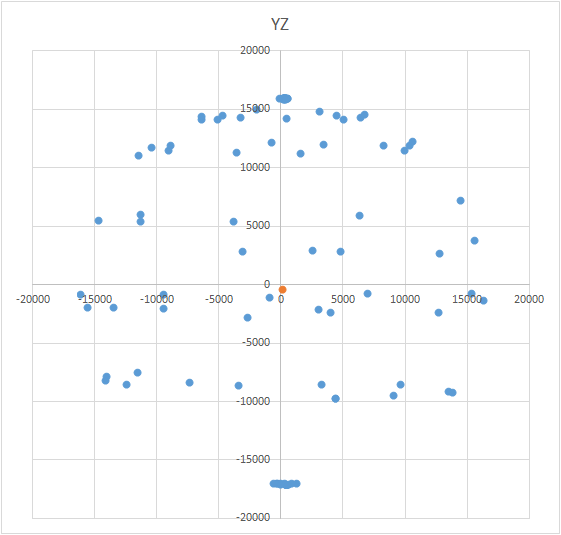Como R, precisamos levar o valor teórico do vetor de influência externa - para o acelerômetro, essa é a aceleração da gravidade, para a bússola - essa é a magnitude média do campo magnético da Terra, para o giroscópio - a velocidade de rotação da Terra. Obviamente, na fórmula deve haver valores de uma dimensão (unidades convencionais do sensor ou m / s 2, graus / s, etc.). É mais conveniente converter em unidades arbitrárias do sensor correspondente.Como calcular um determinado valor nas unidades padrão do sensor?= * / ( — )
: 16- ±2g ?:
9,8 /2 * 65536 / (2g + 2g) = 9,8 /2 * 65536 / (2 * 9,8 /2 + 2 * 9,8 /2) = 16384 . . .
A propósito, se você conhece exatamente o raio da bola, pode calcular o centro apenas pela sua “cunha”. Ou seja, em pontos localizados apenas em um pedaço da superfície da bola. Mas este não é o nosso caso.Como acelerar a busca pelo centro da bola?
É necessário procurar o centro não no cubo inteiro (as dimensões da bola), mas ao longo da linha, cujo início é arbitrário, cada ponto seguinte fica mais próximo do centro real e o final está no centro. Suponha que partimos do ponto (0; 0; 0) ... Sempre nos movemos com um passo constante. Portanto, se imaginarmos um conjunto de cubos 3x3x3, em que cada face é igual ao tamanho da etapa e também imaginarmos que a posição atual é o cubo do meio, teremos 9 + 8 + 9 opções para colocar o próximo ponto. Nós apenas temos que estar em cada ponto, para calcular em qual dos 26 pontos vizinhos o erro será menor. Se o erro for menor no ponto atual e não em um dos vizinhos, significa que ele está no centro e a pesquisa terminou.
Como pode estar no códigoPublic Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai, B + bi, C + ci, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
Exit Do
End If
A = A + ai_min
B = B + bi_min
C = C + ci_min
Loop
. . .
De que outra forma acelerar a busca pelo centro da bola?
Precisa pesquisar com passo variável. Primeiro, procuramos o centro em grandes etapas. Encontramos o centro, reduzimos o passo e a partir dele começamos a procurar mais. E assim por diante, até obter o resultado da precisão necessária.Como pode estar no códigoPublic Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
step = 1000
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai * step, B + bi * step, C + ci * step, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
step = step / 10
If step < 0.01 Then
Exit Do
End If
Else
A = A + ai_min * step
B = B + bi_min * step
C = C + ci_min * step
End If
Loop
. . .
Sobre erros de medição
Durante as medições, pode haver situações em que, por algum motivo, o resultado da medição possa estar muito mais distante da superfície da bola. Ou pode haver muitos pontos. Ou, em geral, o resultado das medições pode não ser uma bola, mas um "ovo" ou um "dirigível". Nesse caso, é claro, você precisa repetir todas as medições, identificando as possíveis causas de erros. Por exemplo, para um magnetômetro, ele pode ser um parafuso ou um prego em uma mesa e você está fazendo medições diretamente acima dele. E quanto mais baixo você abaixa o sensor ao longo do meridiano, mais forte o metal afetará o resultado. Portanto, é necessário determinar o limite do valor de erro permitido. Para não refazer as medições devido a vários pontos claramente errados, você pode aplicar um filtro. O princípio do filtro é muito simples - depois de calcular o centro pela primeira vez, classifique os pontos pelo nível de erro em cada um deles.Alguns dos pontos com o maior erro podem ser simplesmente descartados (por exemplo, 10%). Então você precisa repetir a busca pelo centro.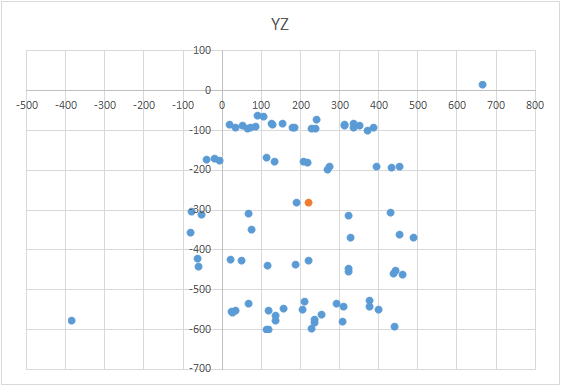
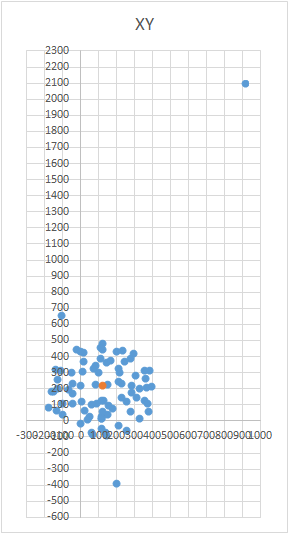
Total
O método tem uma precisão muito boa. O método permite que você faça com meios improvisados simples (bola, banco, etc.). Funciona rápido o suficiente. Código simples. Muitos sensores possuem registros especiais nos quais você pode escrever o valor encontrado e o sensor subtrai-o rapidamente. Esses registradores geralmente têm o prefixo "TRIM", como no MPU9260, ou "OFFSET", como no LSM303. Mas o conhecido LIS302DL não possui esses registros.Não se esqueça de colocar um sinal de mais, se você gostou. Escreva nos comentários seus métodos para calibrar sensores.