🖖🏾 🐋 👩🏾‍🤝‍👨🏼 Luz comprimida ou o que tem ondas gravitacionais 🌈 😐 🛩️

Olá GT! Hoje falaremos sobre um estado incomum de luz e suas aplicações igualmente incomuns. Bem-vindo ao gato.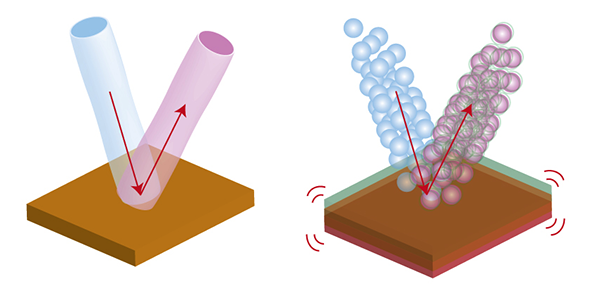

Um policial para Heisenberg que excedeu a velocidade.
"Você sabe o quão rápido você estava dirigindo?"
"Não, mas eu sei exatamente onde eu estava."
(anedota barbada)

A relação de incerteza de Heisenberg proíbe medir simultaneamente a coordenada e a velocidade (momento) de uma partícula. Além disso, ninguém se preocupa em medir com precisão uma das quantidades - mas a segunda incerteza se torna ainda maior.

Em geral, as relações de incerteza são bastante comuns na física. Por exemplo, a mesma relação é verdadeira para uma onda eletromagnética: relaciona sua intensidade (= número de fótons) e fase :

Devido a esta incerteza, não podemos medir com precisão o sinusóide descrito pela onda, pois o observador estará sempre na neblina:

Isso pode ser mostrado visualmente em um gráfico de pizza, em que a amplitude corresponde ao raio do ponto, fase - o ângulo entre a direção do ponto e o eixo X. O verde mostra a incerteza:

Nesse caso, ninguém se preocupa em determinar com precisão a amplitude ou a fase. Então o círculo de erros se transformará em uma elipse, encolhendo em uma direção e se estendendo na outra:

Essa condição é chamada de luz comprimida , porque as flutuações de amplitude ou fase são compactadas ao longo de um dos eixos, reduzindo o erro de medição. O primeiro é chamado de compressão de amplitude (a elipse é esticada através do raio, é possível medir com precisão a amplitude nos máximos e mínimos da onda senoidal); a segunda fase (elipse ao longo do raio, você pode medir a fase nos zeros da onda senoidal).

Por que isso é importante?

Para a luz comum, não podemos medir a amplitude ou a fase com mais precisão do que o círculo de erros nos fornece. Isso é chamado de nível de ruído quântico padrão . A luz compactada permite reduzir o erro em uma direção e "mergulhar" sob esse nível de ruído. De certa forma, podemos [pathos_mode_on] tomar medidas mais precisas do que a natureza gostaria [pathos_mode_off].

Um exemplo simples.

Toda fonte de luz gera um número inteiro de fótons a cada segundo. Pode mudar de um segundo para o outro devido à natureza quântica da luz, formando a distribuição do número de fótons (mencionei isso na história de Hanbury Brown e Twiss ).

O número de fótons é igual à intensidade da luz. Ou seja, a intensidade é um pouco de "ruído" - varia de segundo para segundo. Este é o nível de ruído quântico padrão.

Mas se o número de fótons não mudar de segundo para segundo (figura à direita), a intensidade será estritamente constante e desprovida de ruído. Esta será a luz que é maximamente comprimida em amplitude. O fluxo de fótons ao mesmo tempo é mais ou menos assim:

Ou seja, os fótons são emitidos estritamente periodicamente. Se a periodicidade for violada, a luz ainda permanece em certa medida compactada.

Por que isso é necessário?

Ao contrário de outros objetos exóticos, o uso de luz compactada se mostrou muito promissor.

Telecom. A transmissão de informações modulando uma variável compactada (amplitude (AM) ou fase (FM), o termo mais geral em quadratura) permite aumentar a taxa de sinal / ruído. É possível construir amplificadores que adicionam ruído apenas àquela quadratura que não é compactada e que não transmite um sinal útil.

Emaranhamento quântico. Em alguns casos, paralelos podem ser traçados entre o emaranhado de fótons e a compressão da luz. Por exemplo, você pode confundir dois feixes de luz: um comprimido em amplitude, o segundo em fase.

Criptografia quântica. Provém do emaranhamento quântico e da imagem acima. No esquema mais simples da criptografia quântica, Alice transmite informações para Bob usando fótons com polarização aleatória. A direção da compactação pode desempenhar o papel de compactação: se for selecionada incorretamente, um invasor que intercepte o canal de comunicação medirá o ruído em vez do sinal.

Detectores de ondas gravitacionais. Para esta tarefa, você precisa capturar as menores flutuações de grandes cargas. Isso geralmente é feito usando um interferômetro Michelson. É construído de maneira muito simples: um laser, dois espelhos e uma placa translúcida:

Um laser é refletido a partir de dois espelhos, duas reflexões interferem e um padrão de interferência se forma na tela. Se um dos espelhos se mover, a imagem também se moverá. Isso acontece devido a uma mudança na fase da onda: o espelho se afastou - o caminho do laser ficou um pouco mais longo, uma fase adicional entrou - as tiras de interferência mudaram.

Como o interferômetro mede a fase, sua resolução não pode ser melhor que a incerteza da fase. Para um laser convencional, ele é limitado a um nível de ruído quântico padrão. Porém, se substituirmos o laser por uma fonte de luz compactada em fase, esse problema desaparecerá e poderemos medir distâncias com precisão sem precedentes.

Hoje, isso é feito em um dos maiores detectores de ondas gravitacionais GEO600 e, aparentemente, está planejado para o detector espacial LISA. A propósito, entre os usuários do GT, há Shkaff , que está fazendo isso e está pronto para responder às suas perguntas nos comentários.

Medição de fase precisa. A luz comprimida por fase pode ser útil para medições usando o método de contraste de fase, uma técnica cotidiana da biologia moderna.

Como gerar?

Criar luz compactada não é tão simples. Para isso, são utilizados processos ópticos não lineares. É muito difícil explicar nos dedos, mas vou dar um exemplo.

Em alguns cristais, observa-se um efeito chamado não linearidade de Kerr - a dependência do índice de refração da intensidade da luz. Vamos enviar um pulso de laser para esse cristal. Para qualquer pulso, a intensidade nas frentes é menor que no centro - o que significa que o índice de refração mudará mais fortemente onde o centro do pulso está agora. A diferença nos índices de refração leva ao fato de que a fase da onda no centro e nas frentes varia de maneira diferente. A totalidade dessas mudanças leva ao fato de que a fase se define um pouco melhor que o normal, e a intensidade - pelo contrário, um pouco pior. Olá, luz apertada :).

Como detectar?

A luz compactada também pode ser medida de várias maneiras.

1. Esquema Hanbury Brown-Twiss.

Em uma série sobre Hanbury Brown e Twiss, eu disse que a função de correlação g ⁽²⁾ corresponde à largura da distribuição do número de fótons. A compressão da amplitude da luz significa que o número de fótons é determinado melhor que o normal. Portanto, no sentido amplo da palavra g ^{(2), é} menor que a unidade - um sinal de luz espremida.

2. Detector de balança. É como um circuito Hanbury Brown-Twiss, mas em vez de correlações, subtraímos ou adicionamos sinais de dois diodos (a nosso pedido):

Um espelho translúcido transmite ou reflete cada fóton aleatoriamente. Essa aleatoriedade introduz ruído quântico adicional (como ruído de tiro) no sinal . Esse ruído tem um sinal diferente em dois diodos: se um fóton é refletido, ele não voa; se voar, não será refletido.

Se subtrairmos o sinal de um diodo de outro, o ruído quântico não irá a lugar algum. E se somarmos? Então o barulho desaparecerá, porque tem um sinal diferente. (Outra explicação: dividimos a luz em duas partes e depois as dobramos - isso, obviamente, não adicionou ruído adicional.)

Portanto, a subtração nos adiciona ruído com um nível quântico padrão, e a adição não muda nada. Se a luz estudada foi comprimida em amplitude (ou seja, “silenciosa”), a subtração a tornará mais barulhenta e a adição a deixará inalterada. Alternando entre adição e subtração, podemos medir o nível de ruído e, se for diferente, observamos a luz comprimida pela amplitude.

O ruído após adição (vermelho) e subtração (azul) é mais ou menos assim. O ruído vermelho é muito mais fraco e corresponde à luz compactada.

3. Homodyning. A compactação de amplitude é fácil de medir, mas e a compactação de fase? Se for possível "girar" a orientação da elipse (ou seja, a fase da luz), a luz da fase espremida se tornará espremida em amplitude. A fase pode ser girada misturando a luz com a onda de referência. Isso é muito semelhante ao oscilador local do receptor, apenas no oscilador local a frequência das ondas de referência e estudadas é diferente, mas no oscilador local não é (daí o nome).

Mesmo no homódino, você precisa selecionar a fase da onda de referência. Em eletrônica, isso é feito por um deslocador de fase, em óptica por uma linha de atraso (quanto mais tarde a luz chegar, mais a fase funcionará). A mistura ocorre no mesmo espelho translúcido:

A onda de referência vem de baixo. E então - o mesmo detector equilibrado.

E de interessante

Até agora, a luz compactada é usada apenas em interferometria ultra-precisa. O problema é que é incrivelmente frágil. Isso é fácil de entender pelo exemplo da luz ideal ampliada por amplitude (o fluxo de fótons é estritamente periódico):

Na propagação da luz, as perdas são inevitáveis, sempre acidentais. Isso significa que os fótons desaparecerão do fluxo aleatoriamente:

Como você pode ver, quase nada resta da periodicidade. Bem como da compressão. Portanto, a luz compactada é muito difícil de transmitir a longas distâncias.

E finalmente, vamos admirar o esquema do detector gravitacional GEO 600 perto de Hannover:

A fonte de luz compactada está em um fundo amarelo. Utiliza um processo óptico não linear, mas não a não linearidade de Kerr, mas a geração do segundo harmônico da radiação. A linha pontilhada vermelha é luz compactada. Acima, à direita, há um interferômetro Michelson com ombros de 600 metros; os espelhos estão suspensos em cargas que devem oscilar das ondas gravitacionais. A imagem do interferômetro é obtida no fotodiodo no canto inferior direito.

Fontes de
M. Fox. Ótica quântica: uma introdução - Oxford University Press, 2006.
Agradecimentos a Shkaff pelos comentários dos especialistas.

Imagens gratuitas : KDPV , 1 , 2 , 3 , 4 , 5 , 6, 7 , 8 , 9 , 10 .