Pergunte a Ethan No. 78: por que E = mc2?
A equação mais famosa de Einstein é calculada mais lindamente do que se poderia esperar.
Resulta da teoria especial da relatividade que massa e energia são manifestações diferentes da mesma coisa - um conceito desconhecido da mente comum.
- Albert Einstein
Alguns conceitos científicos estão tão mudando o mundo e são tão profundos que quase todo mundo sabe sobre eles, mesmo que eles não entendam completamente. Por que não trabalhar juntos? Toda semana você envia suas perguntas e sugestões, e essa semana escolhi uma pergunta de Mark Liyuv, que pergunta:Einstein derivou a equação E = mc 2 . Mas unidades de energia, massa, tempo e comprimento já eram conhecidas antes de Einstein. Então, como fica tão bonito? Por que não há constante para duração ou tempo? Por que não é E = amc 2 , onde a é alguma constante?Se nosso Universo não tivesse sido organizado como está agora, tudo poderia ter sido diferente. Vamos ver o que eu quero dizer.
Por um lado, temos objetos com massas: das galáxias, estrelas e planetas às menores moléculas, átomos e partículas fundamentais. Embora sejam minúsculos, cada um dos componentes do que nos é conhecido sob o nome de matéria tem uma propriedade fundamental da massa, o que significa que, mesmo que excluamos seu movimento, mesmo que o reduzamos a uma parada completa, ainda afetará todos os outros objetos do universo.
Especificamente, exerce força gravitacional sobre todo o resto do Universo, não importa a que distância esteja o objeto distante. Ele desenha tudo para si mesmo, é atraído por todo o resto e também possui a energia inerente à sua própria existência.A última afirmação é contra-intuitiva, uma vez que a energia, pelo menos na física, é mencionada como a possibilidade de fazer algo - a capacidade de fazer o trabalho. E o que você pode fazer se ficar parado?Antes de responder, vamos olhar para o outro lado da moeda - coisas sem massa.
Por outro lado, existem coisas que não têm massa - por exemplo, luz. Essas partículas têm uma certa energia, e isso é fácil de entender, observando sua interação com outras coisas - quando absorvidas, a luz transfere sua energia para elas. A luz com energia suficiente pode aquecer a matéria, adicionar energia cinética (e velocidade), levar elétrons a níveis mais altos de energia ou até ionizar, dependendo da energia.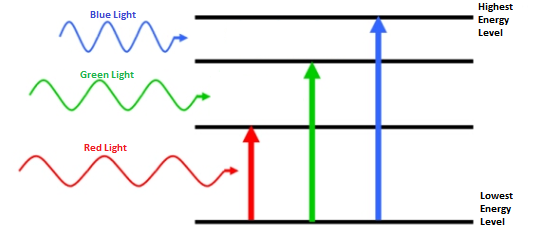
Além disso, a quantidade de energia contida em uma partícula sem massa é determinada apenas por sua frequência e comprimento de onda, cujo produto é sempre igual à velocidade da partícula: a velocidade da luz. Isso significa que as ondas mais longas têm frequências mais baixas e menos energia, enquanto as curtas têm frequências e energia mais alta. Uma partícula maciça pode ser desacelerada, e as tentativas de extrair energia de uma massa sem massa levarão apenas a uma extensão de sua onda, e não a uma mudança de velocidade.
Tendo isso em mente, vamos pensar como a energia em massa pode ser equivalente ao trabalho? Sim, você pode pegar uma partícula de matéria e uma antimatéria (elétron e pósitron), juntá-las e obter partículas sem massa (dois fótons). Mas por que as energias de dois fótons são iguais às massas de um elétron e um pósitron multiplicadas pelo quadrado da velocidade da luz? Por que não há outro fator, por que a equação exatamente iguala E e mc 2 ?
O que é interessante, de acordo com o SRT, é que a equação simplesmente deve se parecer com E = mc 2 , sem nenhum desvio. Vamos falar sobre os motivos disso. Primeiro, imagine que você tem uma caixa no espaço. É imóvel e possui espelhos nos dois lados, e por dentro há um fóton voando para um dos espelhos.
Inicialmente, a caixa não se move, mas como os fótons têm energia (e momento), quando o fóton colide com o espelho em um lado da caixa e pula, a caixa começará a se mover na direção em que o fóton se moveu originalmente. Quando o fóton atinge o outro lado, ele ricocheteia no espelho do outro lado, alterando o momento da caixa para zero. E continuará sendo refletido dessa maneira, enquanto a caixa se moverá no meio do caminho em uma direção e a outra metade permanecerá imóvel.Em média, a caixa se moverá e, portanto, como possui massa, terá uma certa energia cinética, graças à energia do fóton. Mas também é importante lembrar o impulso, o momento do objeto. O momento do fóton está relacionado à sua energia e comprimento de onda de maneira muito simples: quanto menor a onda e maior a energia, maior o momento.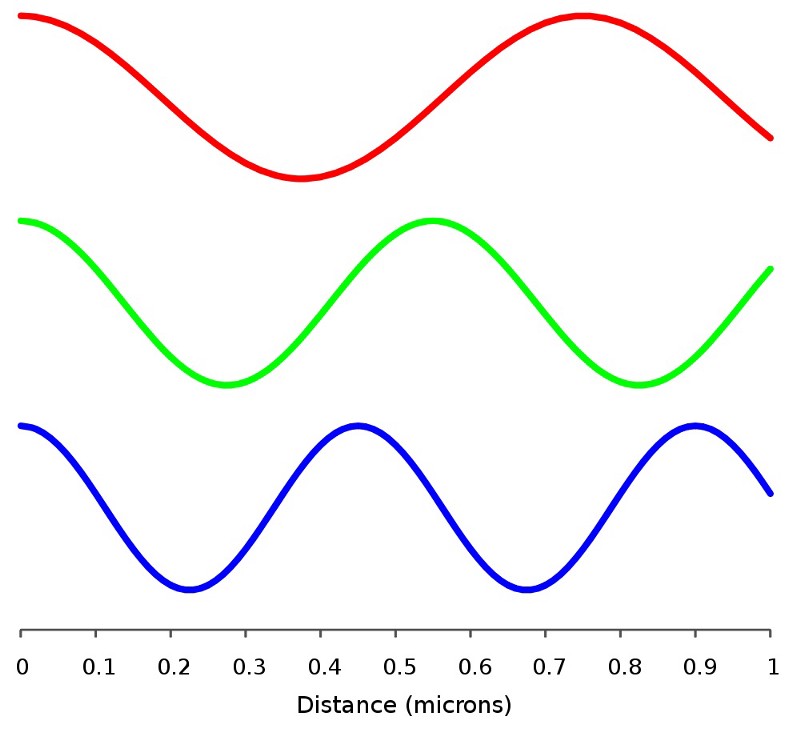
Vamos pensar no que isso significa e, para isso, realizaremos outro experimento. Imagine o que acontece quando apenas o fóton se move inicialmente. Ele terá uma certa quantidade de energia e momento. Ambas as propriedades devem ser preservadas, para que no momento inicial a energia do fóton seja determinada pelo seu comprimento de onda, e a caixa tenha apenas a energia restante - seja ela qual for - e o fóton tenha todo o momento do sistema, e o momento da caixa é zero.
Então o fóton colide com a caixa e é absorvido temporariamente. Momento e energia devem ser conservados - estas são as leis básicas de conservação do Universo. Se o fóton é absorvido, existe apenas uma maneira de manter o momento - a caixa deve se mover a uma certa velocidade na mesma direção em que o fóton estava se movendo.Até agora, tudo bem. Só agora podemos nos perguntar qual é a energia da caixa. Acontece que, se seguirmos nossa fórmula usual para energia cinética, K E = ½mv 2 , presumivelmente conhecemos a massa da caixa e, com base no conceito de momento, sua velocidade. Mas se compararmos a energia da caixa com a energia do fóton, que ele possuía antes da colisão, veremos que a caixa tem energia insuficiente.Um problema? Não, é bem simples de resolver. A energia do sistema caixa / fóton é igual à massa restante da caixa mais a energia cinética da caixa mais a energia do fóton. Quando uma caixa absorve um fóton, a maior parte de sua energia é destinada ao aumento da massa da caixa. Quando a caixa absorve um fóton, sua massa muda (aumenta) em comparação com o que era antes da colisão.Quando a caixa novamente emite um fóton na outra direção, recebe momento e velocidade ainda maiores (que são compensados pelo momento negativo do fóton na direção oposta), ainda mais energia cinética (e o fóton tem energia), mas perde parte da massa restante em troca. Se tudo for calculado (existem três maneiras diferentes de fazer isso e também há uma descrição), você descobrirá que a única transformação de massa que permite economizar energia e momento será E = mc2 .
Se você adicionar qualquer constante, a equação deixará de ser equilibrada e você perderá ou ganhará energia toda vez que emitir ou absorver um fóton. Tendo descoberto a antimatéria na década de 1930, vimos diretamente a confirmação de que a energia pode ser convertida em massa e vice-versa, e os resultados das transformações coincidiram exatamente com E = mc 2 , mas foi através de experimentos mentais que essa fórmula pôde ser derivada várias décadas antes das observações. Somente alinhando o fóton com a massa efetiva equivalente a m = E / c 2 , podemos garantir a conservação de energia e momento. E, embora digamos E = mc 2 , Einstein primeiro escreveu a fórmula de maneira diferente, atribuindo a massa equivalente em energia a partículas sem massa.Então, obrigado pela maravilhosa pergunta, Mark, e espero que esse experimento mental o ajude a entender por que precisamos não apenas da equivalência de massa e energia, mas também porque há apenas um valor possível para a "constante" nessa equação, que ajudará a preservar energia e momento - e é isso que o nosso universo exige. A única equação que funciona é E = mc 2 . Envie-me suas perguntas e sugestões para os seguintes artigos.Source: https://habr.com/ru/post/pt396379/
All Articles