👩🏼‍⚕️ 👨🏽‍⚖️ 🏫 Ficamos em forma: da geometria hiperbólica aos complexos cúbicos e vice-versa 🆖 ❌ ☝️

A prova marca o fim de uma era no estudo de formas tridimensionais.

Há trinta anos, o matemático William Thurston falou sobre sua visão: sistematizando todas as formas tridimensionais finitas possíveis.

Thurston, detentor do Fields Prize, que passou a maior parte de sua carreira nas Universidades de Princeton e Cornell, possuía uma capacidade sobrenatural de representar o inimaginável: não apenas as formas que vivem no espaço tridimensional usual, mas também uma variedade muito maior de formas com propriedades tão complexas que só podem se encaixar espaço com muitas dimensões. Onde outros matemáticos viam o início das formas, Thurston via estruturas: simetrias, superfícies, a relação entre diferentes figuras.

William Thurston em Berkeley em 1991.

"Depois de muitos anos de estudo, muitas pessoas têm a impressão de que a matemática é um assunto estrito e formal que lida com regras complexas e obscuras", escreveu ele em 2009. "A boa matemática é exatamente o oposto disso." A matemática é a arte da compreensão humana ... A matemática canta quando sentimos isso em todo o cérebro. ”

A visão de Thurston foi baseada em um casamento entre duas abordagens aparentemente díspares para o estudo de figuras tridimensionais: geometria, um reino familiar de ângulos, comprimentos, regiões e volumes e uma topologia que estuda as propriedades de formas independentes de medições geométricas precisas - propriedades que não são mudando se o formulário for esticado ou torcido, como uma " alça ".

Para um topologista, a superfície da panela é equivalente à superfície de uma mesa, lápis ou bola; a superfície do copo é equivalente a uma rosquinha ou toro. Do ponto de vista de um topologista, a variedade de formas bidimensionais - superfícies - se resume a uma lista simples de categorias: esférica, toroidal e toroidal com um grande número de orifícios. (A maioria de nós apresenta esferas e toros como tridimensionais, mas, como os matemáticos os consideram superfícies ocas, eles consideram essas superfícies objetos bidimensionais, medidos por área de superfície e não por volume).

A idéia principal de Thurston era entender os três manifoldspossível através da união de geometria e topologia. Assim como a categoria topológica de 2 variedades, contendo a superfície de uma frigideira e um lápis, também contém uma esfera ideal, Thurston sugeriu que muitas categorias de variedades 3 contenham uma instância, uma variante 3 cuja geometria é tão homogênea e perfeita, tão bonita que, como Walter Neumann, da Columbia University, ela "toca como um sino". Além disso, Thurston sugeriu que os formulários que não possuem esse exemplo podem ser cortados em pedaços nos quais já serão.

Em um artigo de 1982, Thurston apresentou sua “hipótese de geometrização” entre 23 perguntas sobre 3-variedades que ofereciam aos matemáticos a direção do conhecimento de formas tridimensionais. (Havia 24 perguntas na lista, mas uma delas, ainda não resolvida, é mais como um beco intrigante do que a estrada principal).

"Thurston tinha um enorme talento para fazer as perguntas certas", diz Vladimir Markovich, matemático da Caltech. "Todos podem fazer perguntas, mas raramente acontece que uma pergunta leve a insights e beleza, assim como as perguntas de Thurston foram bem-sucedidas".

As perguntas inspiraram uma nova geração de matemáticos, dezenas dos quais decidiram conduzir seu trabalho sob a direção de Thurston. Seus "filhos" matemáticos expressam seu estilo, como escreveu Richard Brown.da Universidade. John Hopkins. "Eles olham para a matemática, como crianças em uma feira: com alegria e surpresa, fascinados por cada nova descoberta, e estão felizes em fazer parte de tudo".

Dezenas de anos após o surgimento do trabalho de Thurston, os matemáticos seguiram seu "mapa" da pesquisa, e sua motivação foi alimentada não tanto pelas aplicações possíveis de suas descobertas quanto pelo bom lugar que os três coletores ocupavam no estudo de formas. As formas bidimensionais são bastante comuns, são fáceis de descrever e dividir em categorias. Formas de quatro, cinco e mais multidimensionais são praticamente impossíveis de serem treinadas: a variedade de possibilidades é tão grande que os matemáticos se limitaram a conhecer apenas suas subclasses especiais. E no caso de formas tridimensionais de estrutura, por um lado, são misteriosas e difíceis, mas, por outro, são fundamentalmente reconhecíveis.

O trabalho de Thurston já passou 30 anos e todas as questões, exceto quatro, já foram resolvidas, incluindo a hipótese de geometrização, comprovada pelo matemático russo Grigory Perelman em 2002, que foi uma conquista marcante na matemática moderna. Mas as quatro tarefas restantes resistiram teimosamente.

"O fato de não termos sido capazes de resolvê-los por tanto tempo significa que algo muito profundo está escondido lá", disse Yair Minsky, da Universidade de Yale.

Finalmente, em março de 2012, Ian Aigol, da Universidade da Califórnia em Berkeley, despertou a comunidade matemática ao anunciar a prova da hipótese Wise que cobria as últimas quatro perguntas de Thurston de uma só vez.

Os matemáticos chamam esse resultado de fim de uma era.

"A visão das 3 variedades descrita por Thurston em seu trabalho naquela época pode ter parecido fantástica, mas agora está totalmente realizada", diz Danny Calegari, da Caltech. "Suas idéias foram surpreendentemente comprovadas - e todos os detalhes estavam corretos."

"Pareceu-me que havia um conhecimento especial e métodos especiais de pensamento que só me eram peculiares", escreveu Thurston, tendo recebido o prêmio de matemática Steele apenas alguns meses antes de sua morte, em agosto de 2012, aos 65 anos . "E estou muito feliz por ter atingido tal nível quando isso não é assim - muitas pessoas compartilharam minha maneira de pensar e muitas provaram os teoremas que eu empreendi sem sucesso".

A conquista de Aigol mostra a existência de um esquema simples para a construção de todos os três manifolds hiperbólicos compactos - o único tipo de formas tridimensionais que ainda não foi totalmente explicado.

"Agora entendemos exatamente como são as três variedades", disse Henry Wilton, da London University College. "Este é o culminar de uma enorme história de sucesso matemático".

Estudo de superfície

O programa de Thurston tentou fazer com três variedades o que os matemáticos fizeram com sucesso cem anos atrás com variedades bidimensionais. Para nos esticarmos antes de entender os coletores tridimensionais, vamos dar uma olhada no interior da classificação de superfícies “compactas orientáveis” (superfícies finitas sem perfurações e cortes com orientação constante).

Para abordar o problema de classificação, os matemáticos mostraram que, para qualquer superfície, é possível realizar sua simplificação seqüencial cortando-a ao longo das curvas até que ela se abra em um polígono plano.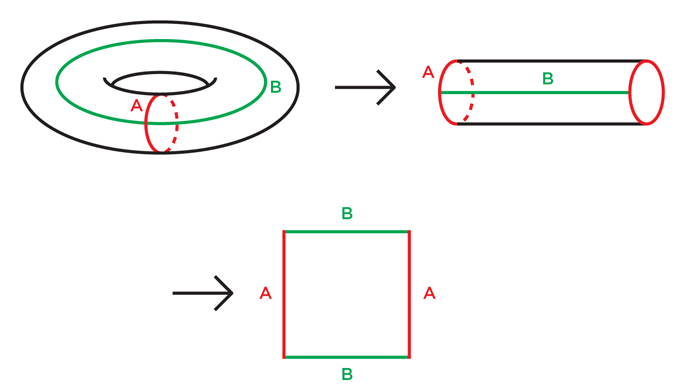

Fig. 1 1

É fácil mostrar isso para um toro: primeiro cortamos ao longo do loop A, como na Fig. 1, obtemos um cilindro. Depois cortamos o laço B, endireitamos o cilindro em um quadrado. A figura 2 é um pouco mais difícil de entender, mas mesmo lá, o corte ao longo de quatro curvas transforma um toro duplo (um toro com dois orifícios) em um octógono. Da mesma forma, para qualquer toro com n orifícios, podemos fazer 2n entalhes nos loops e expandi-lo para 4n-gon.

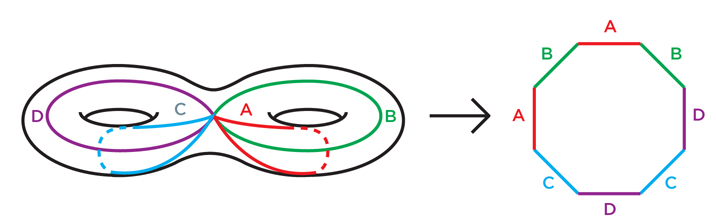Fig.2

Você pode tentar simplificar uma superfície indefinida arbitrária (e identificá-la) cortando-a de maneira semelhante. Se essa não é uma esfera, os topologistas mostraram que ela deve conter loops internos (loops que não se cruzam) que não podem ser puxados para um ponto - como A e B no toro. Cortar uma superfície ao longo de um desses loops remove várias propriedades topológicas interessantes da superfície. Os matemáticos mostraram que, para reduzir a superfície a um polígono plano, é necessário cortá-la um número finito de vezes.

Tendo simplificado a superfície ao nível do polígono, é fácil ver que, se colarmos suas bordas para restaurar a superfície original, teremos que fazer um toro, ou um toro duplo ou um triplo, etc. Afinal, a primeira colagem transformará o polígono na superfície da vista do túnel, e cada uma subseqüente adicionará um novo túnel ou simplesmente costurará partes abertas. Quando terminamos o processo, obtemos um toro com alguns buracos.

Essa abordagem não apenas demonstra a equivalência topológica de uma superfície com uma esfera ou algum toro: também fornece uma maneira de dotar uma superfície de uma estrutura geométrica simples e uniforme.

A esfera, obviamente, já possui uma estrutura geométrica unificada: sua geometria parece a mesma em qualquer lugar da esfera. A superfície da rosca, pelo contrário, não é de todo uniforme: a região da borda externa da rosca é dobrada de maneira semelhante a uma esfera, e a região do anel interno é dobrada como uma sela.

E não importa como você coloque o toro no espaço - não importa como você o estique e torça - você não poderá fazê-lo para que a geometria seja a mesma em qualquer lugar. Algumas partes arredondam-se como uma esfera, outras como uma sela, outras podem ser planas.

É possível, no entanto, equipar o toro com uma estrutura geométrica abstrata que seja idêntica a qualquer momento - basta declarar que em cada uma das pequenas seções do toro as distâncias e ângulos são determinados pela medição do quadrado a partir do qual, como vimos, o toro pode ser feito. Um toro físico no espaço comum, cujos comprimentos e ângulos correspondem a essa regra abstrata, não pode ser construído, mas essa definição de comprimentos e ângulos é internamente consistente. Como o quadrado tem a geometria plana (euclidiana) usual, dizemos que o toro pode ser equipado com uma estrutura euclidiana. Um toro com essa geometria se assemelha a um videogame no qual um personagem desaparece do lado esquerdo da tela e reaparece no lado direito, e desaparece do lado superior, aparece na parte inferior.

Tentando fazer esta operação com um toro duplo, encontraremos um obstáculo. Lembre-se de que podemos fazer um toro duplo colando as bordas de um octógono. Se declararmos que a geometria do toro duplo é copiar a geometria do octógono, encontraremos o problema de seus ângulos. Depois de colar o octógono em um toro duplo, os pontos de canto serão colados, em um ponto do toro duplo. Neste ponto, haverá oito ângulos, cada um adicionando 135 graus, que juntos serão 1080 graus em vez de 360.

Se tentarmos dar a estrutura geométrica do octógono ao toro duplo, acontece que nosso toro duplo terá a geometria euclidiana usual em todos os lugares, exceto por um ponto em que sua superfície se projeta como um chapéu pontiagudo (os pontos de canto não são um problema se colarmos um quadrado em um toro: colamos quatro ângulos retos e obtenha os 360 graus perfeitos).

Para obter uma estrutura geométrica suave no ponto de canto do toro duplo, é necessário que cada um dos oito ângulos contribua apenas 45 graus em vez de 135. É interessante que esse octógono exista, mas não viva no plano euclidiano usual, mas em outra estrutura chamada disco hiperbólico: o terceiro um tipo de geometria uniforme e consistente internamente, como esférica ou euclidiana. Mas, como é mais difícil de imaginar, ela foi descoberta pelos matemáticos apenas no início do século XIX.

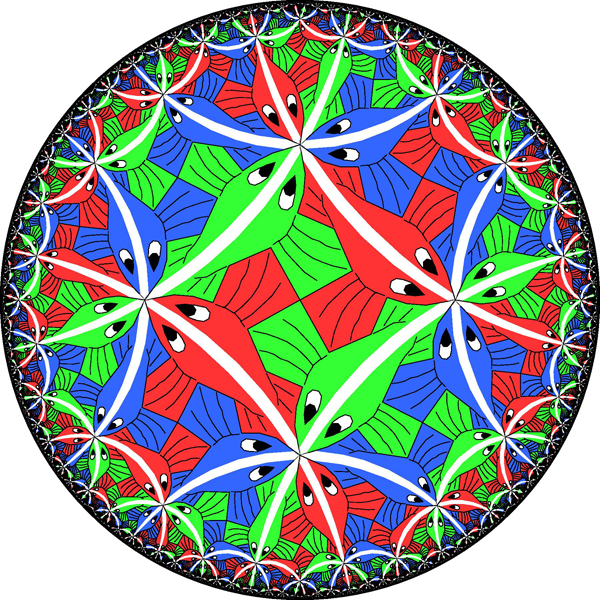Fig.3

Grosso modo, a geometria hiperbólica (ou geometria de Lobachevsky) é obtida se declararmos que todos os peixes da Fig. 3 são do mesmo tamanho. Pode-se imaginar que a Fig. 3 é na verdade uma imagem de disco obtida através de uma lente distorcida, o que torna o peixe mais próximo da borda menor do que o peixe do meio. Em um verdadeiro disco hiperbólico na frente da lente, todos os peixes têm o mesmo tamanho.

No espaço comum, é impossível fazer um disco hiperbólico regular e suave para que todos os peixes sejam realmente iguais. Mas, de um ponto de vista abstrato, a regra do tamanho do peixe fornece uma geometria internamente consistente e com a mesma aparência em qualquer ponto - não para um observador com uma lente distorcida, mas do ponto de vista de um residente de um disco hiperbólico.

Na geometria hiperbólica, o caminho mais curto, ou "geodésico", entre dois pontos, é o caminho pelo menor número possível de peixes. Esse caminho é sempre um semicírculo perpendicular ao limite do disco. Exemplos são semicírculos ao longo dos espinhos dos peixes. Do nosso ponto de vista distorcido, esses caminhos são curvos, mas para um residente do disco essas são linhas retas. Como Thurston disse, para dirigir ao longo dele, você não precisa girar o volante. Diferentemente do plano euclidiano, no qual as linhas paralelas sempre permanecem à mesma distância, em um disco hiperbólico duas linhas disjuntas podem divergir rapidamente muito uma da outra.

Do ponto de vista da geometria hiperbólica, as figuras na Fig. 4 são octógonos comuns com lados retos. Em um desses octógonos, todos os ângulos de 45 graus são exatamente o que precisamos para um toro duplo. Se colarmos corretamente os lados deste octógono, obtemos um toro duplo com uma estrutura hiperbólica ideal e uniforme.

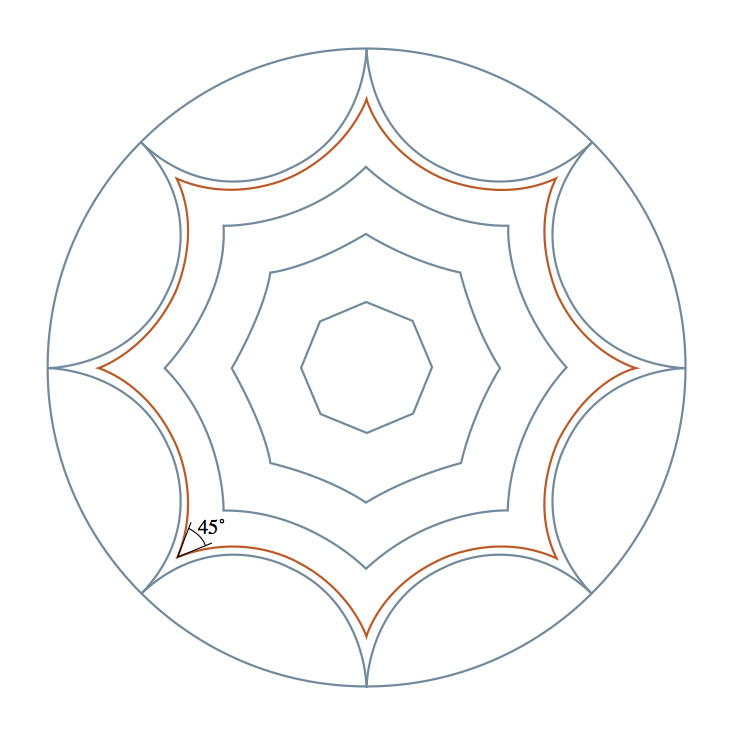Fig. 4

Da mesma forma, podemos equipar o toro triplo com uma estrutura hiperbólica. O toro triplo pode ser colado a partir de 12 gons; portanto, se fizermos 12 gons hiperbólicos com ângulos internos de 30 graus, sua geometria hiperbólica pode ser transferida suavemente para o toro triplo. Continuando o tema, podemos fornecer um toro com 4 furos, com o quinto e assim por diante, geometria hiperbólica. Nossa classificação de superfícies compactas é a seguinte: uma superfície com geometria esférica (esfera), outra com euclidiana (toro) e infinitas superfícies com geometria hiperbólica (todos os toro com mais de um orifício).

Nos últimos cem anos, essa classificação deu aos matemáticos um método muito proveitoso de transferir questões topológicas sobre superfícies para o domínio geométrico e vice-versa. A classificação de superfícies é a principal idéia no estudo de formas bidimensionais, uma descoberta usada por todos os outros estudos como ponto de partida.

Próxima medição

Os manifolds 3 são muito mais diversos que os 2 e os problemas com eles são mais complicados. Mesmo uma pergunta simples como a famosa conjectura de Poincaré - que pergunta se a versão tridimensional da esfera é a única forma tridimensional compacta na qual cada laço pode ser puxado para um ponto sem se prender ao buraco - permaneceu sem solução por quase cem anos após sua formulação por Henri Poincaré em 1904 ano.

Thurston, porém, sugeriu com ousadia que é possível criar uma classificação de formas tridimensionais semelhante à classificação existente de bidimensional.

As geometrias euclidianas, esféricas e hiperbólicas bidimensionais têm pares em três dimensões. Mas em três dimensões, a lista de geometrias “bonitas” não se limita a elas. Existem geometrias híbridas que são hiperbólicas ou esféricas em certas direções e euclidianas em outras. Em geral, existem oito tipos diferentes de geometrias em três dimensões, uniformes no sentido de que a geometria parece a mesma em qualquer ponto do espaço.

Thurston sugeriu que, assim como as superfícies, os três manifolds podem ser comparados com as estruturas geométricas naturais. Especificamente, ele sugeriu que se você cortar um coletor múltiplo compacto em pedaços de uma maneira especial, cada um poderá ser associado a uma das oito geometrias.

"O objetivo era unificar totalmente a topologia e a geometria em três dimensões", diz Minsky.

A abordagem natural para essa "hipótese de geometrização" foi tentar algo semelhante ao que fizemos com superfícies que cortamos ao longo de curvas até que revelassem todas as propriedades topológicas interessantes e até que fossem simplificadas para um polígono plano. Para coletores 3, uma abordagem semelhante será cortá-los ao longo de superfícies até que, esperançosamente, eles se simplifiquem em um poliedro, cujos lados opostos possam ser colados para obter a forma original. E se podemos construir esse poliedro usando a geometria correta, podemos transformar essa geometria em sua forma original, como foi o caso das superfícies.

Lembre-se de que, no caso de superfícies, cada curva tinha que atender a dois requisitos: a curva não se cruza consigo mesma (os matemáticos dizem que deve ser "embutida") e deve ser, como chamamos, topologicamente interessante, ou seja, cercar alguns os detalhes topológicos da superfície para que não possam ser puxados até um ponto (esse requisito garante que o corte ao longo dessa curva simplifique a topologia da superfície).

Em 1962, o matemático Wolfgang Haken provou que um coletor múltiplo pode ser simplificado para um polígono se o coletor 3 contiver uma superfície cujo corte satisfaz duas condições: ele deve ser incorporado e "incompressível", ou seja, qualquer topologia interessante uma curva na superfície também será topologicamente interessante no contexto mais geral do 3-manifold circundante.

Por exemplo, um toro não será incompressível no espaço tridimensional comum, já que o loop que passa pela abertura do toro é topologicamente interessante do ponto de vista da superfície do toro, mas no espaço tridimensional pode ser compactado para um ponto. Por outro lado, um toro é incompressível dentro de um distribuidor múltiplo, o que pode ser obtido espessando a superfície do toro, de modo que deixa de ser infinitamente fino. Para ser incompressível, cada característica topológica da superfície deve refletir alguma topologia interna do distribuidor múltiplo. Agora, um distribuidor múltiplo que possui uma superfície incompressível incorporada é chamado de distribuidor Haken.

Se o nosso coletor múltiplo tiver uma superfície incompressível integrada, o corte ao longo dele revelará algumas topologias interessantes e nos dará um coletor simplificado. Além disso, Haken mostrou que, se um coletor contiver uma dessas superfícies, o novo coletor obtido ao cortá-lo também será um coletor Haken: ele também terá uma superfície de corte incompressível incorporada. E após um número finito de tais etapas, como Haken mostrou, todas as características topológicas interessantes do coletor original serão cortadas e um simples poliedro permanecerá.

No final da década de 1970, Thurston mostrou que é possível equipar o poliedro resultante com uma das oito geometrias oito-dimensionais, de forma que ela seja transferida suavemente para o polígono recém-colado, combinando perfeitamente nos cantos e bordas do poliedro. Em outras palavras, Thurston provou sua hipótese de geometrização para aquelas variedades cuja decomposição padrão leva a peças que são variedades Haken.

Infelizmente, para um distribuidor múltiplo compacto e arbitrário, não há garantia de que ele tenha essa superfície. No final da década de 1970 e no início da década de 1980, Thurston convenceu a comunidade de que os 3 coletores que contêm uma superfície incompressível incorporada (coletores Haken) são exceções, não regras.

A busca pela prova da hipótese de geometrização para variedades que não sejam variedades de Haken paralisou os matemáticos por mais de vinte anos. Finalmente, em 2002, Perelman apresentou sua prova com base em áreas da matemática muito distantes das estudadas pela maioria dos seguidores de Thurston. (Parece que a prova de Perelman também tocou na hipótese do centenário de Poincaré, o que levou o Instituto de Matemática de Clay a oferecer a ele um prêmio de um milhão de dólares em 2010 - que ele rejeitou imediatamente por razões complexas).

A prova de Perelman foi um ponto de virada, combinando, como Thurston sonhava, topologia e geometria. Agora, cada problema topológico associado a 3 variedades tem um par geométrico e vice-versa. Mas o teorema de Perelman deixou muitas questões importantes não resolvidas sobre quais tipos de 3 variedades podem existir.

Ao classificar 2 variedades compactas (superfícies), os matemáticos não apenas mostraram que cada superfície pode ser equipada com uma estrutura geométrica, mas também fizeram uma lista completa de todas as variedades 2 possíveis. Em três dimensões, faltava uma lista dessas.

Sete das oito geometrias tridimensionais - todas menos hiperbólicas - eram bem conhecidas e, mesmo antes do trabalho de Perelman, os topologistas compilavam uma descrição completa dos tipos de variedades que admitem uma dessas sete geometrias. Essas formas são relativamente simples e poucas.

Mas, como no caso das superfícies, em três dimensões, verificou-se que a maioria dos manifolds é hiperbólica. E a cobertura de um grande número de possibilidades de 3 variedades hiperbólicas foi muito pior entre os matemáticos do que nas outras sete geometrias.

"Dos oito tipos de geometrias, as variedades hiperbólicas são as mais misteriosas e ricas", disse Nicolas Bergeron, da Universidade de Pierre e Marie Curie, em Paris.

O resultado de Perelman disse aos matemáticos que as variedades hiperbólicas eram a última fronteira - o único tipo de variedades 3 que faltava entender. Mas ele não lhes disse como são essas formas hiperbólicas.

Matéria de capa

Mais uma vez, os matemáticos puderam recorrer ao trabalho de Thurston para obter orientação. Sua famosa lista de perguntas continha muitas hipóteses sobre as propriedades de 3 variedades hiperbólicas, que incluíam duas hipóteses diretamente relacionadas à sua aparência: a "hipótese virtual de Haken" e a hipótese do "pacote virtual".

A hipótese virtual de Haken (HHC) afirma que todo distribuidor múltiplo hiperbólico compacto é quase um distribuidor Haken em certo sentido: é possível transformar o distribuidor em um distribuidor Haken expandindo seu número finito de vezes de uma certa maneira. Este novo coletor desdobrado é chamado de "cobertura finita" do coletor original.

Os matemáticos dizem que uma variedade N cobre outra variedade M, se, grosso modo, é possível envolver N em torno de M um certo número de vezes (possivelmente infinito), de modo que cada parte de M seja coberta tantas vezes quanto as outras. Para ser uma cobertura, esse invólucro deve ter várias outras propriedades - por exemplo, N não deve dobrar-se nem rasgar durante o envoltório. Cada pedaço de M é coberto com um monte de cópias idênticas em N. cobrindo-o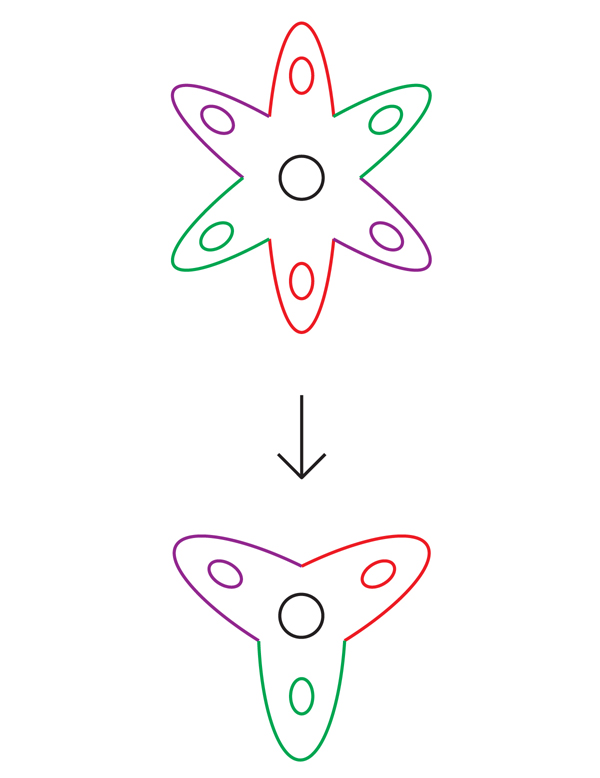

Fig . 5

Por exemplo, a flor de seis pétalas na Fig. 5 cobre uma flor de três pétalas: apenas enrole a flor de seis pétalas duas vezes ao redor da três pétalas. Cada ponto de cor de três pétalas é coberto com dois pontos de seis pétalas. Os matemáticos chamam isso de revestimento de duas camadas.

Da mesma forma, um cilindro infinito cobre o toro: basta enrolar o cilindro ao redor do toro um número infinito de vezes (Fig. 6). Cada ponto do cilindro é coberto: o loop A é coberto por um conjunto infinito de loops distribuídos uniformemente sobre o cilindro, e o loop B é implantado no cilindro em uma linha que segue adiante.

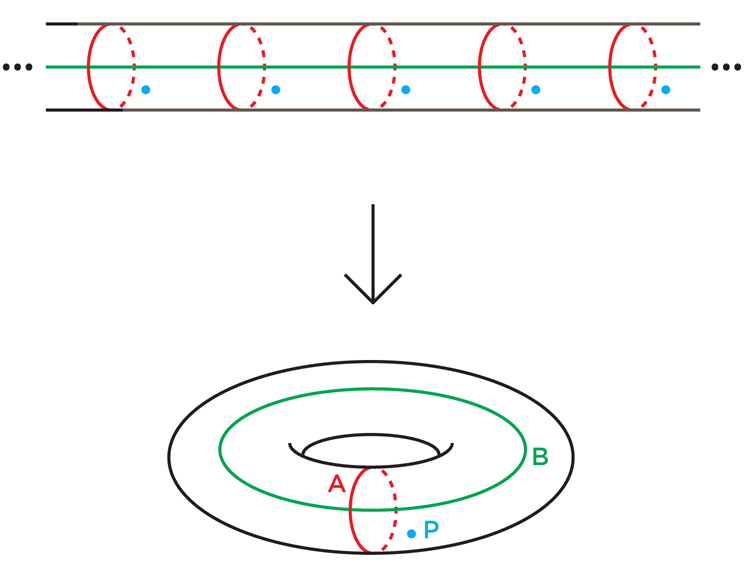Fig. 6 As

topologias da diversidade e suas coberturas estão intimamente relacionadas. Para recriar um coletor a partir de um revestimento de n camadas, você só precisa dobrar o revestimento n vezes. E vice-versa, para recriar o revestimento com base na variedade, você o corta, faz n cópias e cola-o ao longo das bordas (o revestimento de concreto que você recebeu depende da escolha da sequência de colagem).

Uma cobertura preserva algumas propriedades topológicas de uma variedade e revela outras. Um cilindro infinito, por exemplo, lembra que o loop A no toro está fechado, mas esquece que o loop B também está fechado.

Esse processo de implantação levou Thurston à esperança de que, para um distribuidor múltiplo, seja possível cobrir com um número finito de camadas, que será um distribuidor Haken. Já apontamos que não se deve esperar que um coletor triplo hiperbólico compacto arbitrário seja um coletor de Haken (que terá uma superfície incompressível embutida). Mas em 1968, o matemático alemão Friedhelm Waldhausen sugeriu que uma variedade desse tipo deveria conter pelo menos uma superfície incompressível, embora possa passar por si mesma e não ser incorporada.

Nesse caso, argumentou Thurston, pode haver um revestimento final no qual a superfície se desdobre de uma maneira que elimine todas as auto-interseções. Os revestimentos acabados são frequentemente simplificados dessa maneira. Por exemplo, uma vez que a curva na flor de três pétalas na Fig. 7 percorre o orifício central duas vezes, nenhum alongamento e deslocamento pode fazer com que ela não se cruze. Mas se girarmos essa curva em uma flor de seis pétalas, a partir de um certo ponto P, a curva vermelha resultante (que os matemáticos chamam de "subida" da curva original) passará pelo buraco central apenas uma vez e não se cruzará consigo mesma. (Há também um segundo aumento, uma curva azul cruzando o vermelho em dois pontos, fechando o ponto de interseção em uma flor de três pétalas).

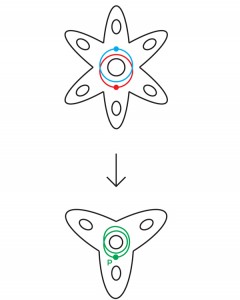Fig. 7

Em um artigo de 1982, Thurston sugeriu que, se tivermos um coletor 3 hiperbólico compacto, deve haver uma maneira de expandi-lo para incorporar superfícies na cobertura finita - ou seja, o coletor 3 deve ser "praticamente Haken".

Como já vimos, um coletor de Haken pode ser construído colando os limites das faces de um poliedro de uma certa maneira. O VGH implica que qualquer distribuidor múltiplo hiperbólico compacto possa ser construído colando primeiro o poliedro corretamente e, em seguida, envolvendo a forma resultante em torno de si um número finito de vezes.

Thurston fez uma suposição ainda mais rigorosa: que todo distribuidor múltiplo hiperbólico compacto pode ser praticamente estratificado, ou seja, ter uma cobertura estratificada finita. Uma variedade que "estratifica sobre um círculo" (como dizem os matemáticos) é construída espessando levemente a superfície, o que a torna tridimensional e colando as bordas interna e externa de qualquer maneira que garanta uma conexão suave das superfícies em cada ponto. (Essa colagem é impossível no espaço comum sem a interseção das partes do coletor resultante entre si, mas abstratamente ainda pode ser estudado). Diz-se que a estratificação dos coletores é possível, porque é possível imaginar como uma superfície espessa é esticada, de modo que as superfícies de contorno divergam muito uma da outra,depois desdobre e puxe-os um em direção ao outro antes de colar, e a variedade resultante se assemelha a uma pulseira com uma conta infinitamente fina na forma de uma superfície em cada ponto do fio da pulseira. Essas contas são camadas.

Cada coletor em camadas é um coletor de Haken, mas não vice-versa. Portanto, a hipótese de pacotes virtuais é mais forte que o VGH, e Thurston não tinha certeza de que isso era verdade. "Essa pergunta questionável, aparentemente, tem uma chance definida de obter uma resposta positiva", é tudo o que ele poderia escrever em uma obra de 1982.

Thurston declarou inicialmente o VGH em uma tentativa inicial de abordar sua hipótese de geometrização, que ele já havia provado para as variedades 3 de Haken. Se o VGH fosse verdadeiro e cada coletor múltiplo compacto fosse uma cobertura finita de Haken, talvez (Thurston esperasse) seria possível usar a estrutura de cobertura geométrica para construir a estrutura geométrica do coletor original.

30 anos depois, muito depois de Perelman provar a hipótese de geometrização por métodos completamente diferentes, o VGH e a hipótese do pacote virtual permaneceram não comprovadas. Eles, juntamente com duas outras hipóteses relacionadas a eles, permaneceram as únicas perguntas sem resposta de 23. Cálculos por computador falaram a favor da validade das coberturas finitas do VGH - Haken para cada um dos 10.000 coletores hiperbólicos selecionados por computador. Este trabalho foi realizado por Thurston e Nathan Dunfield, da Universidade de Illinois em Urbana-Champaign. Mas travar o computador não é prova.

“Quando Thurston apresentou essa hipótese virtual de Haken, essa pergunta parecia fácil. Mas ele resistiu teimosamente à decisão, que esclareceu o quão pouco entendemos nessa área, disse Minsky. "Aconteceu que nossa ignorância nessa direção era profunda."

Superfícies de construção

Em 2009, as águas turvas que cercavam o armazenamento de água e água começaram a ser purificadas. Naquele ano, Markovich e Jeremy Kahn, que trabalhavam na Stony Brook University, anunciaram a prova de um passo fundamental para provar o VHC. O resultado, que chamaremos de "teorema das superfícies incompressíveis", postula que todo distribuidor múltiplo hiperbólico compacto contém uma superfície incompressível (que, possivelmente, cruza consigo mesma e não é incorporada).

A prova de Kan e Markovich é um dos exemplos centrais da interação da topologia e geometria tridimensionais: o teorema das superfícies incompressíveis é uma afirmação puramente topológica, mas Kan e Markovich usaram ativamente outra estrutura retirada da geometria hiperbólica para provar isso.

Para construir a superfície dentro do distribuidor múltiplo, Kahn e Markovich usaram a propriedade de formas hiperbólicas chamadas “mistura exponencial”. Isso significa que, se você iniciar um caminho em algum lugar em uma pequena área dentro do coletor, escolha uma direção e imagine que sua área começa a se mover ao longo do rio que flui aproximadamente na direção selecionada, sua área se espalhará gradualmente e envolverá um coletor 3, para qualquer lugar possível, de qualquer direção possível. Além disso, fá-lo-á muito rapidamente no sentido exato "exponencial".

A propriedade de mistura é única para 3-manifolds hiperbólicos e cresce, grosso modo, pelo fato de que, em contraste com os espaços euclidianos, em um espaço hiperbólico, “linhas retas” ou geodésicas são dobradas uma em relação à outra. Se você selecionar uma pequena área de um disco hiperbólico e permitir que ele se mova na direção selecionada, ele crescerá exponencialmente rapidamente. Dentro de um coletor múltiplo compacto, a região de crescimento também aumentará exponencialmente, mas como o tamanho do coletor é finito, essa região acabará envolvendo-o repetidamente, sobrepondo-se muitas vezes. Além disso - e isso já é mais difícil de provar - a área envolverá o coletor uniformemente, passando por todos os pontos com aproximadamente a mesma frequência.

Os matemáticos lidaram com essa propriedade de mistura exponencial há mais de 25 anos e estudaram cuidadosamente as estatísticas desse “fluxo geodésico”, descobrindo aproximadamente quando e com que frequência uma determinada área passaria em um determinado ponto. Mas até que Kahn e Markovich adotassem o teorema da superfície incompressível adequadamente, os matemáticos não poderiam usar essa propriedade para construir estruturas topológicas em uma variedade (outro matemático, Lewis Bowen, da Universidade Texas A&M, tentou usar a mistura exponencial para construindo superfícies incompressíveis em 3 manifolds, mas seu trabalho se deparou com obstáculos técnicos).

Para ver como a propriedade da mistura exponencial ajuda a construir estruturas topológicas e geométricas, aplicamos-a a uma tarefa mais simples do que a construção de superfícies: a construção de um loop geodésico fechado cujo comprimento é próximo ao nosso grande número favorito (o denotamos por R).

Para criar um loop, selecionamos qualquer ponto de partida no coletor e em qualquer direção inicial e, em seguida, ligamos uma mangueira de rega imaginária localizada em uma área pequena, incluindo o ponto de partida, e a direcionamos aproximadamente na direção selecionada. Gotas de água voam ao longo do caminho geodésico e, enquanto R for grande o suficiente, misturar o fluxo significará que, quando as gotas ultrapassarem a distância R, elas serão distribuídas aproximadamente uniformemente por toda a variedade. Em particular, pelo menos uma gota terá que retornar à área do ponto de partida. Em seguida, construímos uma pequena ponte conectando o geodésico dessa gota ao ponto de partida para obter um loop quase perfeitamente geodésico com um comprimento de cerca de R. É fácil mostrar que, apertando esse loop com mais força no coletor,Você pode obter o loop geodésico perfeito.

Observe que o método nos fornece mais de um único loop geodésico próximo a R. Nesse processo, você pode usar qualquer ponto de partida e qualquer direção, para fazer muitos desses loops. Este é o princípio básico para a construção de estruturas usando mistura exponencial.

A mistura exponencial "afirma que, independentemente das estruturas da diversidade encontradas, você as encontrará em quantidades suficientes", diz Kalegari.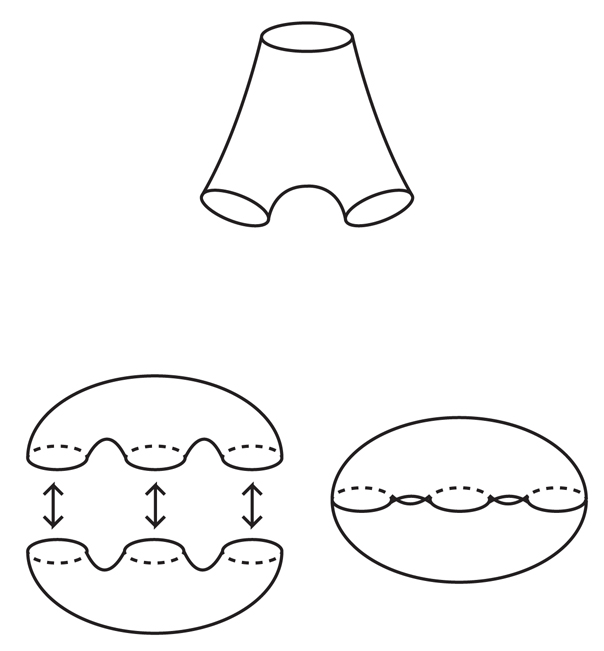

Fig. 8

Kan e Markovich usaram uma abordagem semelhante ao nosso exercício para criar "pares de calças" - superfícies topologicamente equivalentes a uma esfera com três furos (por assim dizer, um para o cinto e dois para as pernas). Essas calças são o material de partida para a construção de todas as superfícies compactas, exceto a esfera e o toro - por exemplo, colar (ou costurar) duas calças nos dá um toro duplo (fig. 8).

Kan e Markovich mostraram que, para qualquer número suficientemente grande de R, é possível construir muitos pares dessas calças dentro do coletor, que seus três “manguitos” se aproximarão do comprimento de R e serão quase completamente geodésicos, ou seja, cada pedaço da superfície das calças parecerá quase o mesmo do ponto vista da geometria hiperbólica.

Eles também mostraram que, para qualquer manguito, as calças têm outro par de calças, saindo do manguito aproximadamente na direção oposta. Costurando essas calças nos punhos, Kahn e Markovic receberam uma grande família de superfícies compactas, quase completamente geodésicas, com pequenas rugas nas costuras. As superfícies quase geodésicas são incompressíveis dentro de seus três coletores; portanto, a construção de Kan e Markovich provou o teorema das superfícies incompressíveis.

Esse método também mostrou que um distribuidor múltiplo possui não apenas uma superfície incompressível, mas "uma estrutura rica de superfícies quase geodésicas em lugares diferentes", diz Kalegari.

O trabalho de Kahn e Markovich lhes trouxe o Prêmio Clay Institute of Mathematics de 2012, concedido por avanços matemáticos.

"As técnicas de Kahn e Markovich não têm interesse inferior aos seus resultados, e este trabalho, sem dúvida, inspirará muitas outras áreas de pesquisa relacionadas a ele", previu Jeffrey Brock, da Brown University, em um artigo de 2011.

Estrutura oculta

Kan e Markovich criaram o ponto de partida para matemáticos que tentam provar o VHC.

Eles mostraram que é garantido que todo coletor contenha uma superfície incompressível. Mas essa superfície pode passar por si mesma, possivelmente em muitos lugares, e não ser incorporada. Para obter o VGHYU com base no trabalho de Kan e Markovich, os matemáticos precisavam encontrar uma cobertura finita do coletor, na qual, exatamente como no exemplo com cores de seis e três pétalas, a superfície sobe para um conjunto de superfícies que não se cruzam (embora possam se cruzar). Se fosse possível, cada um deles seria uma superfície incompressível embutida no revestimento, o que significa que o revestimento seria Haken.

Mas como encontrar essa cobertura?

"Há uma grande lacuna entre o trabalho de Kahn e Markovic e o WHC", diz Danfield. "A descoberta deles foi importante, mas não estava claro se isso ajudaria na busca de superfícies incorporadas".

O trabalho de Kahn e Markovich chamou a atenção de Daniel Wise, da Universidade McGill. Wise fez carreira na pesquisa sobre a remoção de auto-interseções de objetos topológicos usando coberturas finitas, mas ele trabalhou no contexto de "complexos cúbicos", objetos que, à primeira vista, são muito diferentes de 3 variedades. O trabalho de Kahn e Markovich ajudou Wise a mostrar outros matemáticos que esses dois contextos não são tão diferentes.

O complexo cúbico - é o complexo cúbico (CC): é um conjunto de cubos, não apenas um cubo tridimensional é chamado de “cubo” lá, mas também uma forma em qualquer número de dimensões, consistindo em todos os pontos cujas coordenadas estão, por exemplo, nos intervalos entre - 1 e +1. Por exemplo, um quadrado é um cubo bidimensional e um segmento é unidimensional. Cubos na espaçonave são conectados entre si ao longo de cantos, arestas, faces e lados de dimensões mais altas.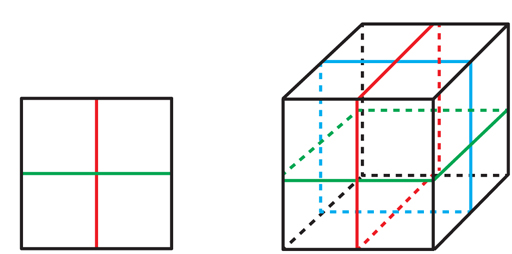

A Fig. 9

CC é muito diferente de 3 variedades - elas nem são variedades, pois as interseções de dois cubos de dimensões diferentes não se assemelham ao espaço usual de nenhuma das dimensões. Porém, os CCs são objetos simplificados nos quais um aspecto-chave da superfície contida em 3 variedades é estudado: o fato de que essa superfície pelo menos localmente divide seu ambiente em duas partes.

Se você precisar explorar objetos que dividem a forma em duas partes, os cubos são o campo natural para começar, por todas as formas possíveis, eles têm o mais simples desses objetos: hiperplanos que os cortam no meio. O quadrado possui dois hiperplanos (GP) - linhas verticais e horizontais, cortando-o ao meio. O cubo possui três GPs (veja a Fig. 9). Um cubo n-dimensional tem n GP se cruzando no centro.

"Os hiperplanos são semelhantes às superfícies em 3 manifolds, mas você os vê instantaneamente", diz Wise. "É difícil procurar superfícies, mas os hiperplanos estão disponíveis para você desde o início."

Se começarmos com um GP dentro de um cubo em um CQ, existe exatamente uma maneira de expandir um GP para um GP em cubos vizinhos; depois disso, existe exatamente uma maneira de expandi-los para os vizinhos; e assim por diante Portanto, para cada GP inicial no CC existe uma maneira única de expandi-lo para o GP em todo o CC (veja a Fig. 10).

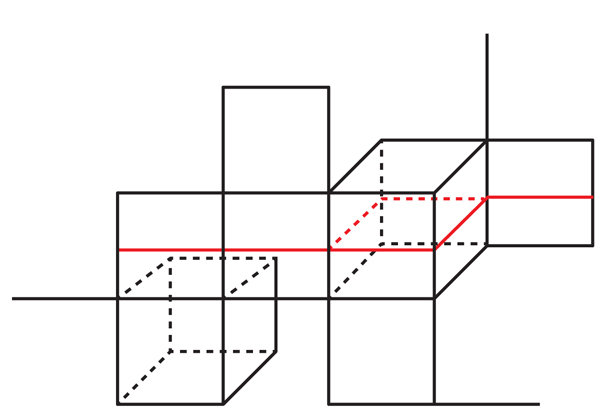Fig. 10. O hiperplano vermelho no quadrado mais à direita se expande exclusivamente para um hiperplano em todo o complexo cúbico.

Essa qualidade contrasta fortemente com os 3 manifolds, nos quais uma pequena área de superfície pode ser estendida para toda a superfície de várias maneiras. O CC com seus GPs é "bonito, claro e estrito", diz Eigol, e eles não têm a "flacidez" de 3 manifolds e suas superfícies.

Quando expandimos o GP na espaçonave, ele pode tropeçar no cubo do qual tudo começou e passar por ele perpendicular ao GP inicial (veja a Fig. 11). Em outras palavras, uma GPU estendida não será necessariamente incorporada. Como é o caso das superfícies dentro de 3 manifolds, pode-se perguntar se o QC possui uma cobertura finita na qual esses GPs com auto-interseção se elevam aos incorporados - esta é a versão da hipótese virtual de Haken para o QC.

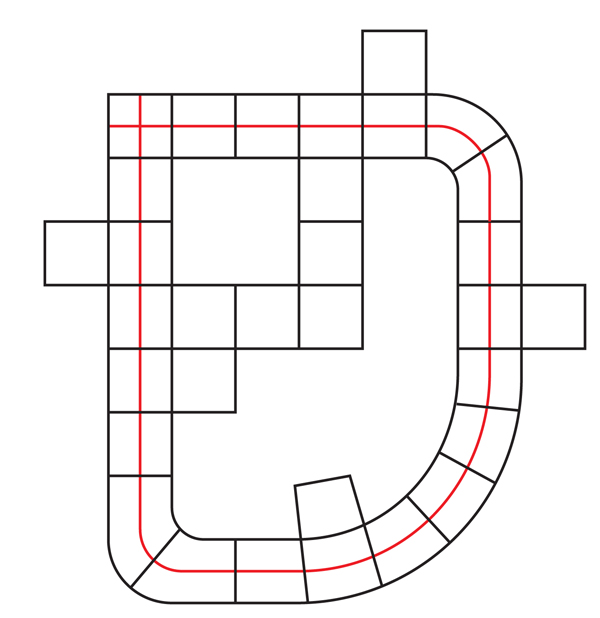Fig.11

Alguns anos atrás, Wise e Frédéric Haglund, da Universidade de Paris-Sul XI, identificaram uma classe de CQs “especiais” que, além de outras propriedades, possuem apenas GPUs integradas. Na última década, a Wise desenvolveu um arsenal de técnicas adaptadas para identificar "QCs especiais". Em 2009, Wise lançou um "trabalho principal" de 200 páginas, como Danfield o chamou, no qual descreveu um conjunto de descobertas relacionadas a QCs especiais, como "teoremas de combinação", mostrando como reunir QCs especiais para garantir novos QCs, também possuindo uma "especialidade". Em seu trabalho, Wise formulou uma hipótese que afirmava, grosso modo, que qualquer CQ com uma geometria dobrada de maneira semelhante a uma geometria hiperbólica é "virtualmente" especial - ou seja, possui uma cobertura finita especial. Essa hipótese foi chamada de hipótese sábia.

Wise estava convencido de que, se esse formulário for de alguma forma semelhante ao CQ - quando puder ser "cubado" -, a estrutura do CQ será a chave para descobrir muitas propriedades do formulário original.

"O CC era um segredo que as pessoas nem sabiam o que perguntar", disse ele. "Esta é uma estrutura oculta fundamental."

Florestas cúbicas

Weise estava extremamente preocupado com o cubo de formulários, mas a princípio seus colegas riram dele por causa dessa mania.

Então Kahn e Markovich provaram o teorema da superfície incompressível, e Wise e Bergeron publicaram imediatamente um artigo mostrando que a existência de superfícies incompressíveis em um coletor 3 hiperbólico compacto fornece um método para cubá-lo - e para que as superfícies do coletor 3 correspondam exatamente aos hiperplanos no complexo cúbico resultante .

A chave para o design de Wise e Bergeron foi o fato de Kahn e Markovich mostrarem como construir não uma, mas muitas superfícies. Seguindo a abordagem ao cubo, formulada pela primeira vez em 2003 por Michael Sageev, agora trabalhando em Technion (Israel), Wise e Bergeron começaram a tomar uma enorme coleção de superfícies de Kahn-Markovich - o suficiente para dividir um coletor de três em polígonos compactos.

Agora imagine um dos pontos de interseção dessas superfícies - por exemplo, existem n superfícies. A conjectura de Sageev era considerar essa interseção como uma sombra, por assim dizer, da interseção de n hiperplanos em um cubo n-dimensional. Um KK correspondente a uma variedade de três é construído, grosso modo, adicionando um cubo n-dimensional para cada interseção de n superfícies (na realidade, tudo isso é construído de maneira mais sutil para levar em conta várias circunstâncias topológicas imprevistas). Dois cubos em um complexo são adjacentes se seus pontos de interseção correspondentes em um coletor 3 forem conectados pela face de um dos polítopos.

"O complexo cúbico é necessário para calcular com precisão como as superfícies se cruzam entre si e entre si", diz Danfield.

Wise e Bergeron mostraram que esse KK é "equivalente homotopicamente" ao coletor original, ou seja, o KK pode ser comprimido e esticado (levando em consideração o achatamento em algumas dimensões e o processo inverso) até que o KK se transforme em um coletor e vice-versa. Além disso, essa equivalência homotópica transforma cada superfície de um coletor 3 no correspondente GP equivalente à homotopia em KK.

O CQ construído dessa maneira satisfaz os requisitos geométricos da hipótese Wise, o que significa que, se a hipótese Wise for verdadeira, esse CQ terá uma cobertura finita na qual todos os GPs serão incorporados.

Se esse revestimento final realmente existir (por exemplo, cobrindo m chapas), precisamos lembrar que o revestimento pode ser construído a partir do próprio QC, cortando-o de uma maneira especial, fazendo m cópias desse QC e colando-os nas linhas de corte. É fácil mostrar que esta receita para a fabricação de um revestimento pode ser transferida para a fabricação de uma cobertura final de um coletor 3 e que nessa cobertura final as superfícies de Kan-Markovich usadas para construir o CC subirão para as superfícies incorporadas. Em outras palavras, se a hipótese Wise for verdadeira, o IHC também será verdadeiro.

“Esse é um compromisso muito estranho: seu QC pode ser, por exemplo, 10.000 dimensional, e pode parecer que, em certo sentido, você está piorando a situação”, diz Wise. "Mas, apesar do valor do CQ, muitas de suas propriedades são muito fáceis de entender, portanto esse procedimento é muito valioso." "Preferimos algo grande, mas bem organizado, em vez de 3 variedades."

Mesmo depois que Wise e Bergeron estabeleceram uma conexão entre QC e VGH, a maioria dos topologistas que estudavam 3-manifolds ficou longe do QC. Talvez porque o trabalho de 200 páginas de Wise tenha sido desencorajador ou porque os CCs fossem muito diferentes de seus espaços usuais.

"Essas idéias eram esotéricas demais para pessoas que emergiam da geometria hiperbólica", diz Bergeron.

Mas um matemático já era bem versado na topologia de 3 variedades, bem como nas coisas combinatórias mais abstratas que Wise usou em sua abordagem.

"Acho que Jan Eigol foi o único especialista em 3 manifolds que entendeu cedo o suficiente como as idéias de Wise poderiam ser usadas para a topologia de 3 manifolds", diz Bergeron.

Eigol aprofundou o estudo do "trabalho principal" de Wise e ficou convencido de que todas as suas partes relacionadas à hipótese de Wise estavam corretas. Aigol está envolvida no VHC há algum tempo; ele percebeu que a abordagem de Wise, transformando superfícies flácidas em hiperplanos cristalinos, era exatamente o que ele precisava.

"A KK nos fornece florestas para a construção do revestimento final", disse ele.

Para construir um revestimento final especial na espaçonave Wise-Bergeron, a Aigol começou a cortar a espaçonave ao longo do GP em "cubos de Lego". Ele então atribuiu cores às faces dos blocos, para que quaisquer duas faces encontradas no canto tivessem cores diferentes. Então, Eigol mostrou que, grosso modo, existe uma maneira de colar um número finito de cópias de cubos de Lego nas faces com as mesmas cores, de modo que as cores nas laterais dessas faces também correspondam. Como resultado, cada GP estendido terá a mesma cor. O CQ resultante será o revestimento final do original e todos os seus GPs serão incorporados, uma vez que quaisquer dois GPs cruzados serão de cores diferentes, portanto, este não será um GP se cruzando.

Em 12 de março, Aigol anunciou a prova da hipótese Wise e, portanto, da hipótese virtual Haken.

"Foi a notícia mais emocionante desde que Perelman comprovou a hipótese de geometrização", disse Danfield.

As informações passaram por uma comunidade de pesquisadores de 3 variedades, e o CQ imediatamente se tornou um tópico comum para todos os topologistas.

"Acho que até agora a comunidade matemática não entendeu o quão poderoso é o trabalho de Wise", disse Aigol. "Acho que meu resultado vai explicar às pessoas o incrível progresso que ele fez".

Agora, de acordo com Wise, os matemáticos estão começando a perceber que "toda vez que você cria algo em cubo, pode revelar todos os tipos de segredos da estrutura".

Fim de uma era

A prova de Aigol da teoria de Wise foi a prova de "4 pelo preço de 1": provou não apenas o VGH, mas também as outras três das 23 perguntas de Thurston, que até então permaneciam em aberto. No período que antecedeu a prova, Eigol e outros matemáticos mostraram que todas as três questões - a hipótese do pacote virtual e mais duas questões técnicas sobre as 3 variedades hiperbólicas - também se seguiram da hipótese Wise.

No caso da hipótese do pacote virtual, lembramos que o objetivo era mostrar que cada coletor hiperbólico compacto 3 possui uma cobertura finita que é entrelaçada em um círculo, ou seja, construída colando as partes opostas de uma superfície espessa. Pelo VGH, sabemos que um coletor possui um revestimento finito de Hakenov - ou seja, o revestimento tem uma superfície incompressível incorporada. Se você abrir o coletor Haken ao longo dessa superfície, obterá algo que parece uma superfície espessa nas extremidades, mas como Deus sabe o que há nas "entranhas".

Yang Aigol em uma recente viagem a Daejeon, Coréia do Sul.

Em 2008, de acordo com Kalegari, houve um “avanço surpreendente” quando a Eigol mostrou que três coletores hiperbólicos que satisfazem condições técnicas especiais são estratificados virtualmente. No ano seguinte, a Wise, com base nisso, mostrou que todos os coletores Haken são praticamente estratificados. Ou seja, existe uma maneira de expandir o coletor Haken para obter uma cobertura finita que revele uma topologia complexa e leve a um coletor foliado simples. Portanto, se o coletor é virtualmente Hakenov, deve ser praticamente estratificado.

"Acho que todo mundo acreditava que o VGH seria verdadeiro, mas a hipótese do pacote virtual parecia menos acessível para nós", disse Kalegari. "Para mim, o fato de que a hipótese de estratificação virtual segue o VGH é um dos lados mais chocantes de toda a história."

Com a prova da hipótese do pacote virtual, "você pode ser tentado e decidir que os 3 manifolds são muito simples porque os manifolds estratificados em um círculo são simples", disse Minsky. "Mas acho que isso nos ensina que as variedades estratificadas em um círculo não são nada simples e mais astutas do que esperávamos."

Ao mesmo tempo, o teorema do pacote virtual significa que existe uma receita simples e informativa para a criação de todos os 3 coletores hiperbólicos compactos: comece com uma superfície espessa, cole sua borda interna e externa com rotações ao seu gosto e dobre o coletor um número finito de vezes.

“Se você me pedisse um distribuidor múltiplo hiperbólico, eu perguntaria de que tipo você precisa - que tipo de pacote e cobertura final? - diz Kalegari. "Agora sabemos que, nesse processo, não perdemos um único distribuidor múltiplo".

Embora os matemáticos precisem de tempo para testar minuciosamente o trabalho de Eigol, muitos deles estão otimistas quanto à aprovação no teste.

"Jan Aigol não é uma pessoa descuidada", diz Minsky.

Agora que, aparentemente, a última pergunta da lista de Thurston foi resolvida, os pesquisadores estão começando a se perguntar como será a região de topologia das 3 variedades em um admirável mundo novo depois de Thurston.

Os matemáticos concordam que terão muito trabalho para encontrar coisas úteis que o CQ pode oferecer para formulários em cubos. E para as três variedades em si, de acordo com a Aigol, chegou o fim da era - e o começo da próxima.

"Na maioria das áreas da matemática, não há um plano que possa traçar o caminho para 20 a 30 anos à frente, como foi conosco", diz ele. Agora, ele sugere, a topologia de 3 variedades e geometria pode se tornar semelhante a outras áreas da matemática nas quais os cientistas tocam e progridem, mesmo sem o luxo de uma grande imagem hipotética do que está acontecendo.

"Novas gerações de matemáticos farão as seguintes perguntas importantes", diz Aigol.

Ficamos em forma: da geometria hiperbólica aos complexos cúbicos e vice-versa