🏍️ ⛈️ 📵 Como fazer previsões científicas 🧚🏾 🈺 👨🏾

Previsões, não chance.Como

fazer previsões de qualquer evento para que cientistas sérios acreditem em você, você se torne famoso e ganhe um Nobel? É muito simples: você precisa convencer os cientistas de que suas previsões são apenas previsões, não acaso. Um curso escolar em teoria das probabilidades é suficiente para isso. Portanto, apenas três pontos precisam ser concluídos.

Ponto 1. Vamos descrever o evento previsto, limitando-o ao tempo e intervalo espacial. Por exemplo, argumentamos que um determinado evento ocorrerá no dia seguinte (intervalo de tempo) dentro de 100 km (intervalo espacial).

Em seguida, precisamos calcular a probabilidade de ocorrência acidental desse evento no intervalo especificado. Existem vários métodos para isso, dependendo do tipo de eventos, sua distribuição, etc. Mas isso deve ser feito e, para isso, indicamos um tempo claro e um intervalo espacial do evento. Indique essa probabilidade por P _chance.

Tentação:Neste ponto, eu realmente quero trapacear, declarando um intervalo igual ao infinito. Ou seja, este evento do outro lado da Terra - estávamos um pouco enganados nas coordenadas, mas o fato de que é um ano depois é um erro no tempo. Mas, infelizmente - é exatamente por isso que precisamos de uma avaliação da ocorrência aleatória. No caso de um intervalo infinito, será muito próximo de 1.

Ponto 2. A seguir, veremos quantos dos eventos previstos ocorreram. E com base nisso, calcularemos a probabilidade de nossas previsões. Ou seja, se no intervalo indicado o evento realmente aconteceu, coloque um mais um, não aconteceu - zero e, portanto, para todas as nossas previsões. Indique essa probabilidade P _antes.

Tentação:Às vezes, um evento não se enquadra no nosso alcance. Mais uma hora, menos um quilômetro. E eu realmente quero contar isso como uma coincidência. Muitos pesquisadores inescrupulosos fazem isso. Mas não - precisamos expandir inicialmente o leque de previsões ou lançar nosso evento fora da contagem como malsucedido.

Dilema: E existe um dilema tão interessante - se aumentarmos o alcance, mais eventos previstos cairão nele. Mas - a probabilidade de coincidência acidental aumentará. Reduzindo o alcance - diminuímos a precisão de nossas previsões.

Análise de avaliação Em seguida, você pode realizar uma análise de avaliação do _caso P. e P _anterior.Se a probabilidade de um evento acidental for muito maior do que o previsto, ou eles forem aproximadamente iguais, então estamos fazendo algo errado. Enganação, fatos adequados - mas não previsões. Se P _caso.muito menos que 1 e P _antes.mais de pelo menos 0,5 - então podemos dizer que o estudo foi bem sucedido. Em seguida, precisamos criar estimativas probabilísticas mais precisas, depois escrever artigos e concorrer ao Nobel. A análise da avaliação será concluída.

Parece-lhe que este artigo é sobre nada, e tudo isso é óbvio para as coisas do pesquisador? Mas, infelizmente, a pesquisa que fiz abaixo mostra um completo mal-entendido dessas coisas por pessoas oficialmente envolvidas na ciência.

Parte Dois: Previsão de Terremotos

Passamos ao estudo da confiabilidade das previsões de terremotos. Fui encorajado a escrever este artigo pela discussão iniciada nos comentários deste post . A essência é a seguinte: uma certa equipe de cientistas acredita que pode prever terremotos, e um dos autores até coloca essas previsões no site . Eu me comprometi a verificar a confiabilidade do ponto de vista estatístico.

Para começar, surgiu a complexidade com os limites das previsões - o autor não indica diretamente em nenhum lugar em que faixa é feita. Ou seja, como entender que esse evento é exatamente o que previmos? Não há resposta em artigos científicos. Além disso, o gráfico de precisão das previsões mostra que os autores consideram eventos bem-sucedidos acima de 1000 km como previsões bem-sucedidas. do ponto previsto.

Mas nós mesmos podemos determinar os limites. Para fazer isso, pegue estas citações de seus trabalhos científicos :

O epicentro do terremoto, até agora, inclui uma área com um raio de cerca de 50 km.

Vemos que o erro em graus (cerca de 100 km) é uma precisão bastante aceitável nas coordenadas. Isso é confirmado pelo gráfico acima. Para o intervalo de tempo, tire o dia com base na seguinte citação:

O tempo do início do suposto terremoto pode variar em ± 13 horas a partir do tempo estimado. Das 1.118 previsões, 978 casos se realizaram no dia em que foram previstas;

Segundo os autores, a precisão alegada de tal previsão:

O sucesso dessas previsões é de cerca de 70 a 80%.

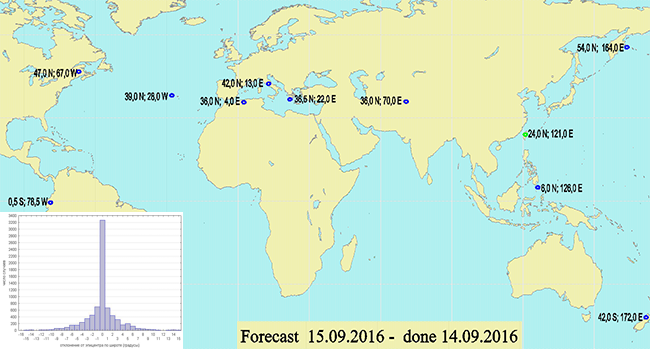
Avaliação independente da previsão.

A avaliação foi realizada em 15 de setembro de 2016 (pude verificar se a previsão realmente apareceu um dia antes do evento e não mudou desde então). Para não criar uma carga no site do autor, anexo uma foto com uma previsão.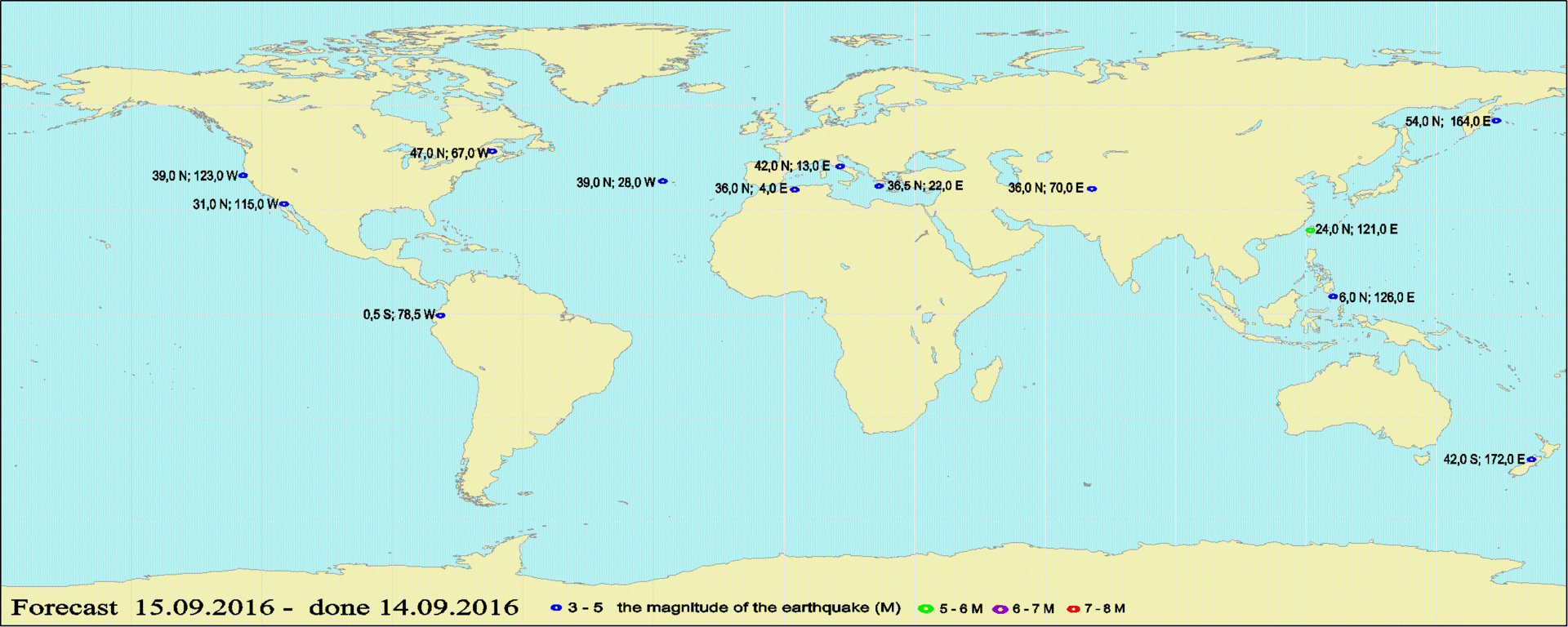

Os dados reais foram obtidos no site da EMSC, que
tem a oportunidade de ver todos os terremotos por qualquer período de tempo, com certas magnitudes. Os dados podem ser baixados na forma de um CSV ou sobrepostos em um mapa do Google:

Vemos uma incompatibilidade completa de dados.Os dados foram coletados para 15 de setembro, foram selecionados todos os eventos com magnitude superior a 3. Se compararmos essas imagens, veremos que os focos não coincidem em dezenas de graus. Lá você nem precisa se aprofundar nos cálculos, nos desenhos, e assim tudo fica claro. Mas você pode fazer uma análise extra. Na tabela da coluna esquerda, estão os dados previstos, à direita - as coordenadas do epicentro mais próximo, se o epicentro estiver mais próximo do que cerca de uma dúzia de graus a partir do ponto previsto.

Predito	Real
24N 121E (grande)
39N 123W
31N 115W
47N 67W
0.5S 78.5W	3.34S 80.8W
39N 28W
42N 13E	42.8N 13.2E
36N 4E
36.5N 22E	40.1N 24.8E
36N 70E
54N 164E
6N 126E	3.8N 129.1E
42S 172E

Dos 13 eventos (um deles é forte), apenas 4 ocorreram dentro de 1000 km. do ponto indicado, e apenas um se encaixa no quadrado reivindicado de 50 km.

Algo coincidiu?

Mas um deles coincidiu com o grau! Aconteceu alguma coisa? Não, tudo é mais simples, não se encaixa aleatoriamente. Como pode ser visto na tabela Nie de terremotos reais, ela tremia todos os dias, começando em 10 de setembro. Portanto, a probabilidade de um evento no ponto indicado para 15 de setembro era muito próxima de 1.

Data	Latitude	Longitude	Magnitude
15/09/2016	42,82	13,19	4.3.
14/09/2016	42,73	13,18	3.2.
13/09/2016	42,58	13,2	3.4.
12/09/2016	42,8	13,22	3.2.
11/09/2016	42,68	13,28	3.3.
09/10/2016	42,79	13,24	3.1.
09/10/2016	42,96	13.16	3.3.
09/10/2016	42,84	13,26	3

Devido à aparente discrepância entre as duas figuras - terremotos previstos e reais, não há razão para conduzir análises adicionais - podemos tirar conclusões.

Conclusão

A julgar pelas estatísticas, as previsões desses cientistas não têm poder. Quem exatamente os autores enganam - pessoas ou a si mesmos, permanece desconhecido. Mas seus gráficos, nos quais mostram a precisão das previsões, não são verdadeiros.

O que, de fato, se correlaciona bem com o trabalho dos cientistas do USGS que, em trabalhos recentes, mostraram a impossibilidade de previsões de curto prazo, já que o sistema é caótico - por causa da estrutura complexa da crosta terrestre, a perturbação cresce exponencialmente. É como com um monte de areia - aspersão em um grão de areia, sabemos que mais cedo ou mais tarde a colina desmoronará (previsões de longo prazo (anos, décadas) são feitas) - mas não sabemos quando exatamente isso acontecerá (curto prazo (dia e horas) não é possível). Cada vez mais interessante , aqui escrito , na seção "Lições do passado, dúvidas e esperanças para o futuro".

Como fazer previsões científicas

Parte Dois: Previsão de Terremotos

More articles: