Em novembro de 2012, Randal Monroe publicou uma história em quadrinhos xkcd com um calendário no qual o tamanho dos números de cada mês era proporcional à frequência com que esse número é mencionado nos livros por seu próprio nome (por exemplo, "14 de outubro") no banco de dados do Google Ngrams desde 2000. A maioria das principais datas são bastante óbvias: 04 de julho , 25 de dezembro , o primeiro dia de cada mês, o último dia de quase todos os meses, e de 11 de setembro , deixando todos para trás. Poucos dias parecem muito menores que o resto. Por exemplo, 29 de fevereiro- um pequeno ponto. Mas se você olhar de perto, poderá ver que o 11º dia de cada mês é relativamente pequeno. Uma nota foi enviada aos quadrinhos: “Em todos os meses, exceto em setembro, o dia 11 é mencionado com muito menos frequência do que o resto das datas. Isso foi até 11 de setembro de 2001, e não sei por que isso acontece. " Vasculhei os dados e acho que descobri o porquê.

No começo, eu tinha certeza de que o 11º é diferente do resto. Um mês pode durar até 31 dias e alguns desses dias certamente serão os menores de todos. Talvez o 11º número do calendário não seja o menor, apenas nossos olhos se apegam a ele. Então eu comparei os dados reais, e não apenas estudei os quadrinhos. O banco de dados Ngrams retorna o número total de vezes que uma frase é mencionada por um ano, normalizada pelo número de livros publicados naquele ano.

Escolhi a quantidade de cada dia do ano (1 de janeiro a 2 de janeiro) e plotei as medianaspor mês para cada dia do mês (1 de janeiro, 1 de fevereiro, etc.) para cada ano. Isso mostrou com que frequência os dias 11 e 30 são mencionados no ano selecionado. A mediana permite suavizar rajadas de dias como 4 de julho. A mediana parecerá incomum apenas se o número de série for muito diferente em pelo menos 6 em 12 meses.

Construí medianas para cada número de série de 2000 a 2008. Abaixo está um histograma para 31 medianas. O primeiro número se destaca de todos e 15 são pouco visíveis entre os demais. Mas o resultado do 11º dia é o mínimo em uma quantidade bastante grande (com um valor P <0,05), o que, à primeira vista, é difícil de explicar.

E essa lacuna existe há muito tempo. O gráfico a seguir mostra todos os números de série para cada um dos anos de 1800 a 2008. Os dados são suavizados por 11 anos para remover o ruído. Mesmo no início, o 11º é muito menor que o grupo principal. Sua pequena falha persiste por várias décadas e, na década de 1860, a 11ª repentinamente se desvia de sua posição como a segunda da série intermediária. A diferença entre o 11º e os números de série comuns aumenta acentuadamente e, como resultado, o valor para a frequência de suas referências se torna aproximadamente metade menor, o que continua na primeira metade do século XX. Na segunda metade, a diferença é reduzida, mas não desaparece até o fim.

Leitores atentos perceberão outra estranheza. Existem mais 4 linhas abaixo do que deveriam ser. De cima para baixo, esses são os números 2, 3, 22 e 23. De 1800 a 1890, são ainda mais baixos que o 11º. Mas, desde 1900, a diferença entre eles diminui, enquanto a diferença desde o 11 começa a aumentar e desaparece completamente na década de 1930. Este também é um tópico bastante interessante, que consideraremos um pouco mais tarde.

Curiosidades tipográficas

Começando o estudo, esperava encontrar um tabu secreto sobre os eventos do 11º dia ou um desvio tipográfico das regras da imprensa. Infelizmente, o motivo acabou sendo muito mais prático: o número 1 é muito semelhante ao I maiúsculo ou l minúsculo (L) na maioria das fontes usadas para imprimir livros. E também 11 pode ser confundido com n. Os algoritmos do Google estão errados, reconhecendo 11 na página e interpretando o número de série como algum tipo de palavra.

Podemos procurar diretamente frases sem sentido, como 11 de março ou 2 de julho ou 2 de maio. 11 pode ser confundido com nove combinações de I, I e I. Cinco deles são realmente encontrados no banco de dados, pelo menos por um mês: II-nd, Il-nd, ii-nd, li-nd e ll-nd. Além disso, havia opções com apenas um caractere errado, 1ª, 1ª e 1ª. Eu chamei esses erros de xxth. Livros do Googlefaz consultas a um banco de dados mais recente que o Ngrams, mas ainda é possível encontrar exemplos desses erros. Por exemplo , o Google reconhece o seguinte como 2 de janeiro:

Como em 11 de fevereiro :

mas em março de li :

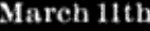existem muitos exemplos no banco de dados. Você pode encontrar outros números de série erroneamente interpretados, mas o dia 11 é muito mais comum que outros.

Acrescentei meus cálculos em 2 de janeiro, 11 de janeiro, etc., e fiz o mesmo nos outros meses. O gráfico a seguir mostra que o 11º recebe um grande impulso com essa adição. Até a década de 1860, a diferença entre o 11º e o grupo principal desapareceu. Após a década de 1860, um terço ou um quarto dessa diferença desapareceu.

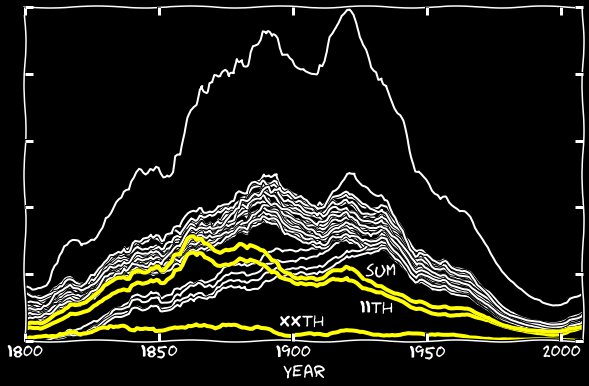E para onde foi o resto do 11º? Desde a década de 1860, o algoritmo do Google começa a cometer um erro estranho - em vez do 11, reconhece os enésimos. Aqui está um exemplo de página preenchida com o enésimo número de janeiro:

em alguns anos, o número de reconhecimentos incorretos excede o número de reconhecidos corretos. Acrescentei o nono dia de janeiro a 11 de janeiro e fiz o mesmo com os outros meses. O gráfico a seguir mostra os números enésimos e sua soma com 11s. Até a década de 1860, sua contribuição era insignificante, mas esse erro começa a ser responsável por quase todos os 11 desaparecidos.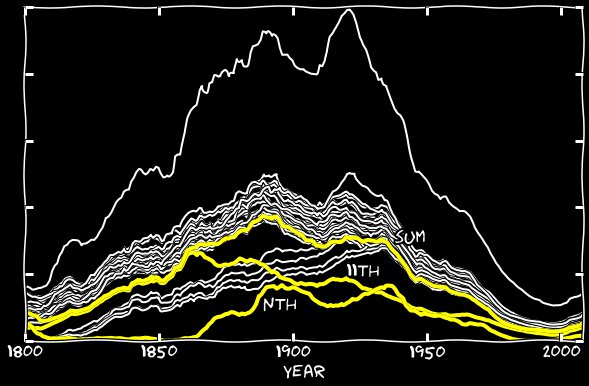

Horário combinado

Adicionando os erros xxth e n-ésimo ao 11º gráfico, fechei a lacuna ao longo de todo o comprimento do gráfico e o 11º começou a parecer o mesmo de todas as outras datas. Acontece que o reconhecimento incorreto do dia 11 na forma do dia n, II, ll e assim por diante, é responsável por um pequeno número de 11 números entre os outros dias do mês.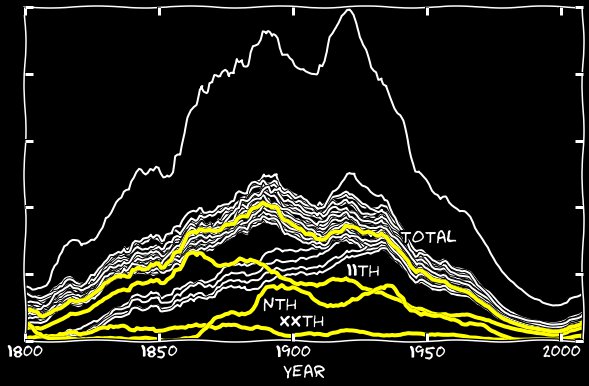

Máquinas de impressão

Embora esteja claro por que o 11º foi mais frequentemente reconhecido incorretamente do que outros, por que o número de erros é tão desigual? O que aconteceu na década de 1860, por causa do qual a taxa de erro aumentou tanto? Suspeito que isso se deva à invenção, na década de 1860, de um dispositivo como uma máquina de escrever. As primeiras máquinas de escrever não tinham uma chave separada para o número 1 . Foi proposto o uso da letra l (L) em letras minúsculas. E quando o algoritmo reconhece o 11 de outubro, na verdade ele faz isso mais corretamente do que pensávamos. Os livros do Google não têm muitos documentos datilografados, mas esse dispositivo popular teve um grande impacto no desenvolvimento de fontes. 1 e eu não diferimos em máquinas de escrever cada vez mais comuns, e até a fonte tipográfica começou a corresponder às expectativas dessa semelhança. Compare esses caracteres em uma fonte1850 : A

diferença entre l sem serifa no topo e 1 com uma serifa óbvia é visível. Compare-os na fonte de 1920 : os

caracteres são idênticos, exceto o kerning. E hoje, a maioria das fontes descreve 1 e 1 como caracteres altos, com duas serifas na parte inferior e uma direcionada para a esquerda, na parte superior. Somente o ângulo de entalhe 1 é um pouco maior que o de l. A qualidade de impressão dos livros desde 1970 ajudou a reduzir o número de reconhecimento incorreto, mas eles não desapareceram completamente; portanto, os problemas restantes apareceram na história em quadrinhos do xkcd.

A questão da popularidade do erro permanece em aberto, na qual 11 é substituído pelo enésimo. Este é um erro bastante estranho. O enésimo é frequentemente encontrado em publicações científicas e matemáticas, e isso pode afetar sua popularidade. Na maioria das fontes, a parte superior de n é muito fina e provavelmente pode não estar visível nos textos em que o algoritmo foi treinado. Mas há uma grande diferença no crescimento de 1 e n, especialmente na era das máquinas de escrever, onde ocorrem muitos erros. Mas a frase nono de janeiro é um absurdo, então as chances de tal reconhecimento deveriam ter sido reduzidas. Talvez alguns textos modernos contivessem erros, e o 11º fosse marcado como enésimo, que serviu de fonte dos erros? A única maneira de descobrir é abrir o código-fonte do algoritmo do Google, que reconhece o texto. Vamos deixar este exercício para o leitor.

Perdeu 2, 3, 22 e 23

Descobrimos os 11º números, mas, durante o estudo do comportamento deles, deparei-me com outro mistério - um número incompreensivelmente baixo de 2, 3, 22 e 23 números, mas apenas até a década de 1930, após trazendo seu número empatado.

No gráfico abaixo estão todos os números, e acontece que nos anos 1800 as datas indicadas não são usadas. As primeiras referências a nossas datas apareceram na década de 1810, seu número cresce na mesma proporção que as outras datas, mas ao mesmo tempo mantém uma lacuna com elas - seu número é cerca da metade do tamanho. De repente, na década de 1890, a lacuna diminuiu, e isso acontece até a década de 1930, quando eles finalmente se fundem no grupo principal.

Estilo pré-revolucionário

Então, os números 2 e 3 no século 19 foram infelizes? O algoritmo do Google dificilmente reconhece duplos e triplos em fontes antigas? Não, acontece que antes, em vez do atual registro em inglês “2º, 3º, 22º, 23º”, era costume escrever “2d, 3d, 22d, 23d”. Criei uma mediana para 2 de janeiro, 2 de fevereiro e outros meses e fiz o mesmo com as datas restantes. O gráfico abaixo mostra a frequência de ocorrência dessas datas no estilo antigo de gravação - elas começam com a frequência de outras datas, mas depois desaparecem gradualmente na década de 1890 e se dissolvem completamente na década de 1930.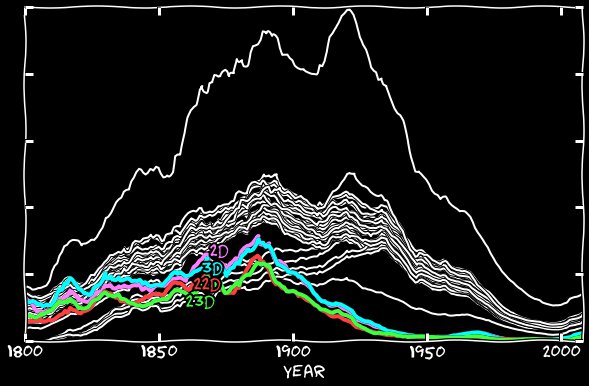

Às vezes, você pode encontrar o uso moderno da forma antiga de gravação, se ela for usada em um título com uma longa história, como a 3d Marine Division. Mas o uso residual desse registro se deve principalmente à existência de reimpressões de livros antigos e publicações de diários antigos.

Horário combinado

Se adicionarmos o estilo antigo ao novo, obteremos o gráfico a seguir. Daqui resulta que datas calculadas corretamente quase não são diferentes de todas as outras.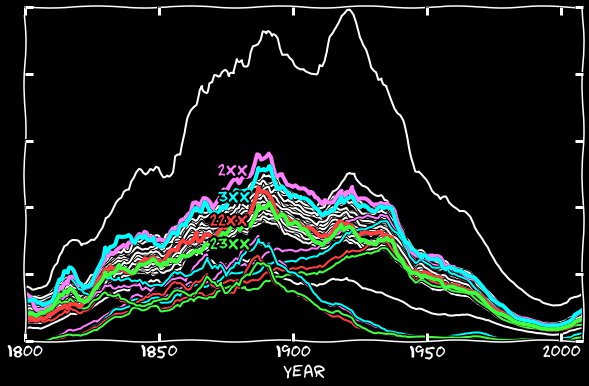

Por que agora acontece que as referências aos números 2 e 3 às vezes excedem os outros em frequência, permanece incompreensível para mim. Penso que, devido à menção frequente do 1º do mês, o 2º e o 3º do dia também devem ser mencionados com um pouco mais de frequência. Mas se você observar as ocorrências de 2 de janeiro ou 2 de janeiro no Google Livros, poderá encontrar algumas dessas passagens:

aparentemente, o Google Livros ignora vírgulas. Portanto, embora as datas do mês de 1 a 4 não sejam nada de especial, esses exemplos aqui podem afetar as estatísticas.

Raciocínio

Por que os escritores usavam essas abreviações de uma única letra antes? Talvez por causa do latim, onde a letra o serviu como um indicador do número de série. Idiomas românticos como espanhol, italiano e português ainda usam o ou a. Ainda usaríamos d se não fosse o 1º, o 4º etc., para os quais a última consoante não seja expressa em inglês com uma letra. Aconteceu que seguir o idioma inglês superava o desejo de imitar o latim.

A perda do décimo primeiro dia do mês e outras datas