Geekly articles weekly

Como cortar justamente um bolo

Cientistas da computação desenvolveram um algoritmo de torta justo para qualquer número de pessoas




Dois jovens cientistas, especialistas no campo da ciência da computação, descobriram como compartilhar honestamente um bolo entre várias pessoas, resolvendo o problema que os matemáticos vêm enfrentando há décadas. Seu trabalho surpreendeu muitos pesquisadores que consideravam impossível essa separação em princípio.

Compartilhar uma torta é uma metáfora para uma ampla gama de tarefas da vida real, incluindo a divisão de um determinado objeto contínuo, seja um bolo ou um pedaço de terra, entre pessoas que valorizam suas propriedades de maneira diferente. Um gosta de uma cobertura de chocolate, o outro quer flores creme. Desde os tempos bíblicos, um algoritmo é conhecido por dividir esse objeto entre duas pessoas, de modo que ninguém inveja a outra: uma pessoa divide o bolo em duas partes iguais para ele, e a outra escolhe um deles. Em Gênesis, Abraão (então conhecido como Abrão) e Ló usaram esse método para dividir a terra, quando Abraão inventou uma separação, e Ló escolheu entre o Jordão e Canaã.

Na década de 1960, os matemáticos criaram um algoritmo para um bolo tão dividido "sem inveja" para três pessoas. Mas até agora, a melhor solução do problema para muitas pessoas foi mais de três procedimentos, estabelecidos em 1995, o cientista político Stephen Brahms [Brams Steven] da Universidade de Nova Iorque e matemático Alan Taylor [Alan Taylor] da Union College. Ele garantiu um compartilhamento “justo” do bolo, mas com uma condição - o procedimento era “ilimitado”, ou seja, o número de etapas necessárias para o compartilhamento seria arbitrariamente grande.

O algoritmo de Brahms-Taylor já foi chamado de avanço, mas "na sua opinião, o seu número ilimitado foi uma grande desvantagem", diz Ariel Procaccia[Ariel Procaccia], cientista da computação da Universidade Carnegie Mellon, um dos criadores do Spliddit , uma ferramenta on-line gratuita para um compartilhamento justo de tarefas, desde tarefas domésticas a taxas compartilhadas de aluguel.

Nos últimos 50 anos, muitos matemáticos e cientistas da computação, incluindo Procaccia, se convenceram de que não há um algoritmo justo e limitado para dividir um bolo em n partes.

"Foi essa tarefa que me levou à área de divisões equitativas", diz Walter Stromkvist[Walter Stromquist], professor de matemática no Brin Mavre College, na Pensilvânia, que obteve bons resultados no problema de compartilhar bolos em 1980. “Durante toda a minha vida, pensei em voltar a esse problema no meu tempo livre e provar que, em princípio, essa extensão do resultado é impossível”. .

Mas, em abril, dois especialistas em ciência da computação refutaram essas expectativas publicando um algoritmo para o compartilhamento justo do bolo com o tempo de operação, dependendo do número de participantes no compartilhamento, e não de suas preferências pessoais. Um cientista, Simon Mackenzie , 27 anos , Ph.D. de Carnegie Mellon, apresentou seu trabalho em 10 de outubro no 57º básico anual de ciência da computação do IEEE.

O algoritmo é extremamente complexo. Uma partição de bolo entre n participantes pode exigir até nn n n n n etapas, com aproximadamente o mesmo número de cortes. Mesmo para um pequeno número de participantes, esse número excede o número de átomos no universo. Mas os pesquisadores já têm idéias para simplificar e acelerar o algoritmo, de acordo com um segundo membro da equipe, Haris Aziz , especialista em ciência da computação de 35 anos da Universidade de New South Wales, que trabalha no grupo de pesquisa de dados australiano Data61.

Especialistas que estudam a teoria da divisão justa , de acordo com o Procaccia, consideram esse "definitivamente o melhor resultado por décadas".

Pedaços de bolo


O algoritmo Aziz e Mackenzie é baseado em um procedimento elegante inventado independentemente pelos matemáticos John Selfridge e John Conway na década de 1960, o que permite dividir um bolo em três.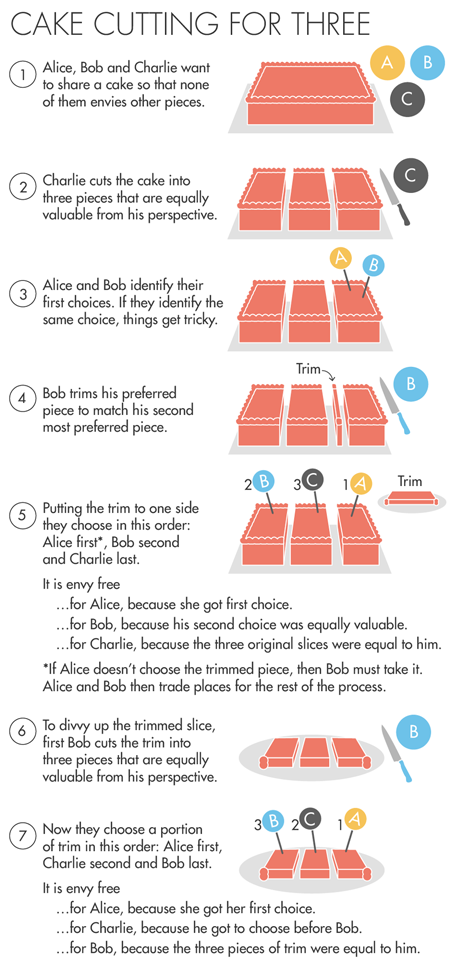



Se Alice, Bob e Charlie (A, B, C) querem dividir o bolo, o algoritmo começa com Charlie dividindo o bolo em três pedaços que parecem iguais para ele. Alice e Bob escolhem as peças que eles gostam. Se eles escolherem peças diferentes - voila, todos conseguem o que querem.

Se Alice e Bob escolhem uma peça, Bob corta uma pequena parte dessa peça para que a peça se torne equivalente, em sua opinião, a outro pedaço de bolo - aquele que Bob escolheria em segundo lugar. O resíduo cortado é adiado. Agora Alice deve escolher a melhor peça para si mesma entre as três restantes e, em seguida, seleciona Bob - com a condição de que ele leve a peça cortada por ele, se Alice não a selecionar. Charlie recebe o terceiro pedaço.

Como resultado, ninguém inveja ninguém. Alice escolheu o primeiro. Bob recebeu uma das duas peças de igual valor para ele. Charlie pegou uma das três peças originais que ele próprio cortou.

Apenas um pequeno corte permanece. Mas ele pode ser dividido sem iniciar o algoritmo primeiro e sem cair em um ciclo interminável de circuncisões e escolhas, já que Charlie está satisfeito com sua peça - e mesmo que quem recebeu a peça cortada receba todo o restante em anexo, por Charlie não pareceria desonesto, porque o pedaço cortado e o restante darão um pedaço de bolo equivalente ao pedaço - afinal, ele cortou esses pedaços desde o início. Aziz e Mackenzie descrevem a posição de Charlie como "dominante".

Agora, se, por exemplo, Alice conseguiu um pedaço cortado, então Bob cortou a guarnição em três partes, o que é equivalente ao seu ponto de vista, Alice seleciona uma dessas peças para si mesma, depois seleciona Charlie e então Bob. Todo mundo está feliz: Alice escolheu primeiro, Charlie pega uma peça melhor que Bob (e ele não se importa com o quanto Alice levou), e do ponto de vista de Bob, todas as três peças são equivalentes.

Brahms e Taylor usaram a propriedade "dominância" (mas com um nome diferente) para desenvolver seu algoritmo de 1995, mas não concluíram sua idéia até que um algoritmo limitado apareceu. Nos próximos 20 anos, ninguém alcançou os melhores resultados. "E não por falta de tentativas", diz Procaccia.

Divisores de bolo não profissionais


Quando Aziz e Mackenzie (A&M) decidiram assumir essa tarefa há alguns anos, eles eram novos na tarefa de compartilhar bolos. "Não tínhamos tanta experiência quanto as pessoas que trabalharam intensamente nisso", disse Aziz. "Embora isso geralmente seja uma desvantagem, no nosso caso foi uma vantagem, porque pensamos de maneira diferente."

A A&M começou estudando a tarefa de dividir em três participantes do zero e, como resultado da análise, chegou a um algoritmo justo e limitado para quatro participantes , publicado por eles no ano passado.

Eles não foram capazes de mostrar imediatamente como expandir seu algoritmo para um número de participantes maior que quatro, mas eles aceitaram essa tarefa com entusiasmo. “Depois de enviar o trabalho para quatro participantes, realmente queríamos continuar rapidamente o trabalho até que alguém mais experiente e inteligente o generalize independentemente para o caso de n participantes”, diz Aziz. E após cerca de um ano, a pesquisa foi bem-sucedida.

Como o algoritmo Selfridge-Conway, o protocolo AiM oferece constantemente diferentes participantes para cortar o bolo em n partes iguais e outros para cortar e escolher pedaços de bolo. Mas existem outras etapas no algoritmo, por exemplo, a troca periódica de pedaços de bolos de uma maneira especial, a fim de aumentar o número de relações dominantes entre os participantes.

Esses relacionamentos permitem que a A&M reduza a complexidade da tarefa. Se, por exemplo, três participantes dominam o restante, eles já podem ser enviados para comer seus próprios pedaços de bolo - eles serão felizes, independentemente de quem receber as sobras. Depois disso, restam poucos participantes e, após um número limitado de etapas, todos ficam satisfeitos e todo o bolo é dividido.

“Olhando para a complexidade do algoritmo, não surpreende que tenha demorado tanto para desenvolvê-lo”, diz Procaccia. Mas a A&M já acredita que pode simplificar o algoritmo para que ele não exija troca de peças e ocorra em apenas n n n etapas. Segundo Aziz, eles já estão trabalhando nesses resultados.

Brahms adverte que mesmo um algoritmo mais simples não terá aplicação prática - afinal, os pedaços de bolo recebidos pelos participantes incluirão muitas migalhas pequenas de diferentes partes do bolo. Essa abordagem não é particularmente útil se, por exemplo, você estiver dividindo a terra.

Mas para os cientistas de matemática e computação que estudam o problema, o novo resultado "redefine todo o tópico", diz Stromkvist.

Agora que os pesquisadores sabem que o bolo pode ser dividido em um número limitado de etapas, o próximo passo, de acordo com o Procaccia, é entender a grande lacuna entre o limite superior do número de etapas pelo método AiM e o limite inferior do número de etapas necessárias para isso. Procaccia já provou anteriormente que o algoritmo para a separação justa do bolo não pode passar em menos de n2 etapas - mas o número de etapas é pequeno comparado com n n n n n n e até n n n .

Aziz diz que os pesquisadores agora precisam descobrir como diminuir essa lacuna. "Eu acho que o progresso pode ser feito em ambas as direções."

Source: https://habr.com/ru/post/pt398683/

More articles:


All Articles