A beleza dos números. Constantes matemáticas na natureza

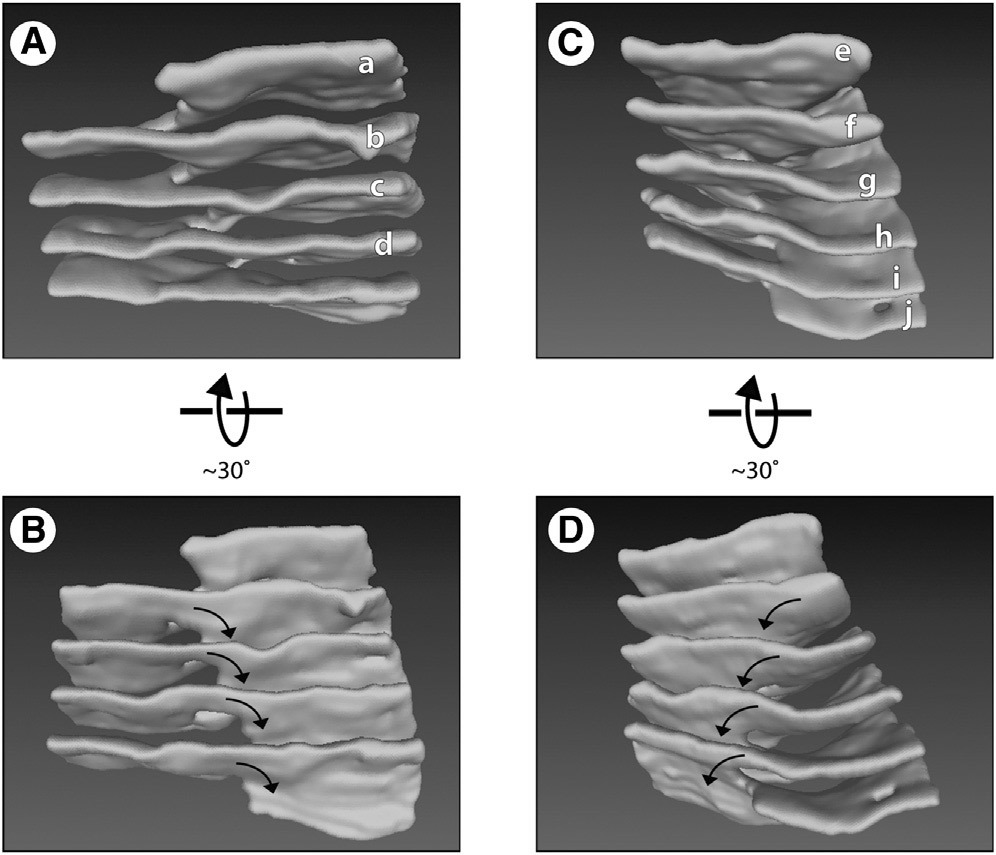Um modelo 3D do retículo endoplasmático de uma célula eucariótica com rampas Terasaki que conectam as folhas planas da membrana

Em 2013, um grupo de biólogos moleculares dos Estados Unidos investigou uma forma muito interessante do retículo endoplasmático - o organoide dentro da célula eucariótica. A membrana desse organoide consiste em folhas planas conectadas por "rampas" em espiral, como se calculadas em um programa de modelagem 3D. Estas são as chamadas rampas Terasaki. Três anos depois, o trabalho dos biólogos foi notado pelos astrofísicos. Eles ficaram impressionados: afinal, exatamente essas estruturas estão presentes nas estrelas de nêutrons. A chamada "pasta nuclear" consiste em folhas paralelas conectadas por formas em espiral.

A incrível semelhança estrutural de células vivas e estrelas de nêutrons - de onde veio? Obviamente, não há conexão direta entre células vivas e estrelas de nêutrons. Apenas uma coincidência?


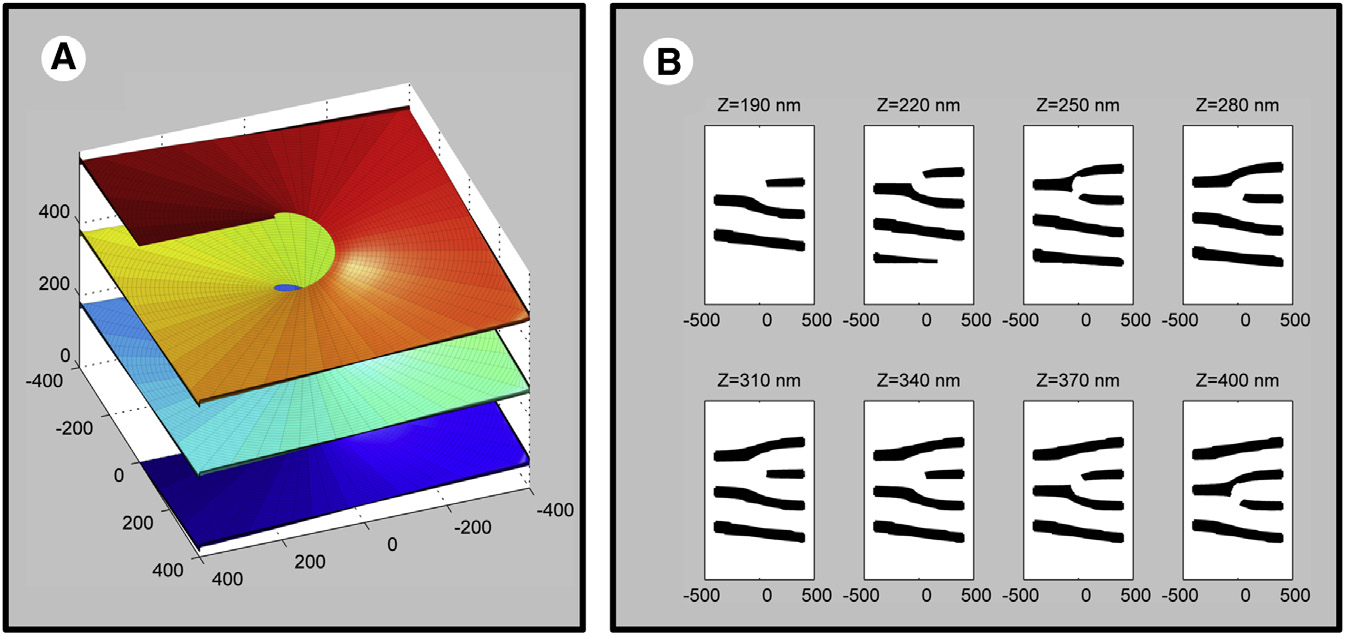Modelo de conexões espirais entre chapas de membrana plana em uma célula eucariótica

Há uma suposição de que as leis da natureza agem em todos os objetos do micro e macrocosmo de tal maneira que algumas das formas e configurações mais ideais pareçam por si mesmas. Em outras palavras, os objetos do mundo físico obedecem às leis matemáticas ocultas subjacentes a todo o universo.

Vejamos mais alguns exemplos que apóiam essa teoria. Estes são exemplos em que objetos materiais essencialmente diferentes exibem propriedades semelhantes.

Por exemplo, buracos negros acústicos, observados pela primeira vez em 2011, exibem as mesmas propriedades que os buracos negros reais devem ter em teoria. No primeiro buraco negro acústico experimentalO condensado de 100 mil átomos de rubídio de Bose-Einstein foi destorcido a uma velocidade supersônica, de modo que algumas partes do condensado cruzavam a barreira do som, enquanto as vizinhas não. O limite dessas partes condensadas simulava um horizonte de eventos de buracos negros, onde a velocidade do fluxo é exatamente igual à velocidade do som. Em temperaturas próximas ao zero absoluto, o som começa a se comportar como partículas quânticas - fônons(uma quase partícula fictícia representa um quantum de movimento vibracional de átomos de cristal). Descobriu-se que um buraco negro "som" absorve partículas da mesma maneira que um buraco negro real absorve fótons. Assim, o fluxo de fluido atua no som da mesma maneira que um buraco negro real atua na luz. Em princípio, um buraco negro sônico com fônons pode ser considerado um modelo peculiar de verdadeira curvatura no espaço-tempo.

Se você olhar mais amplamente as semelhanças estruturais em vários fenômenos físicos, poderá ver uma ordem surpreendente no caos natural. Todos os diversos fenômenos naturais são, de fato, descritos por regras básicas simples. Regras matemáticas.

Pegue os fractais. Essas são formas geométricas auto-semelhantes que podem ser divididas em partes para que cada parte seja pelo menos aproximadamente uma cópia reduzida do todo. Um exemplo é a famosa samambaia de Barnsley.



A samambaia de Barnsley é construída usando quatro transformações afins da forma:



Esta folha em particular é gerada com os seguintes coeficientes: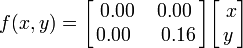









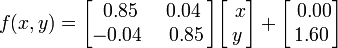
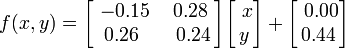Em nosso ambiente, essas fórmulas matemáticas são encontradas em todos os lugares - em nuvens, árvores, cadeias de montanhas, cristais de gelo, chamas oscilantes, na costa do mar. Estes são exemplos de fractais, cuja estrutura é descrita por cálculos matemáticos relativamente simples.

Galileu Galilei, em 1623, disse: “Toda ciência está escrita neste grande livro - quero dizer, o Universo - que está sempre aberto para nós, mas que não pode ser entendido sem aprender a entender a língua em que está escrita. E está escrito na linguagem da matemática, e suas letras são triângulos, círculos e outras figuras geométricas, sem as quais é impossível uma pessoa entender suas palavras; sem eles, ele é como perambular na escuridão. ”

De fato, as regras matemáticas se manifestam não apenas na geometria e nos contornos visuais dos objetos naturais, mas também em outras leis. Por exemplo, na dinâmica não linear da população, cuja taxa de crescimento diminui dinamicamente ao se aproximar do limite natural do nicho ecológico. Ou na física quântica.

Quanto às constantes matemáticas mais famosas - por exemplo, o número pi - é bastante natural que seja amplamente encontrado na natureza, porque as formas geométricas correspondentes são as mais racionais e adequadas para muitos objetos naturais. Em particular, o número 2π tornou-se a constante física fundamental. Ele mostra qual é o ângulo de rotação em radianos, que está contido em uma revolução completa quando o corpo gira. Consequentemente, esta constante é encontrada em toda parte na descrição da forma rotacional de movimento e ângulo de rotação, bem como na interpretação matemática de oscilações e ondas.

Por exemplo, o período de pequenas vibrações naturais de um pêndulo matemático de comprimento L imóvel em suspensão em um campo gravitacional uniforme com aceleração gravitacional g é



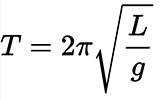Sob condições de rotação da Terra, o plano de oscilação do pêndulo girará lentamente na direção oposta à direção de rotação da Terra. A velocidade de rotação do plano de oscilação do pêndulo depende de sua latitude geográfica .



O número pi é parte integrante da constante Dirac - a constante reduzida de Planck, a principal constante da física quântica, que conecta dois sistemas de unidades - quântica e tradicional. Relaciona a magnitude do quantum de energia de qualquer sistema físico oscilatório linear com sua frequência.



Consequentemente, o número pi está incluído no postulado fundamental da mecânica quântica - o princípio da incerteza de Heisenberg.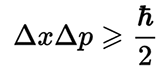



O número pi é usado na fórmula constante da estrutura fina- outra constante física fundamental que caracteriza a força da interação eletromagnética, bem como nas fórmulas hidromecânicas, etc.

No mundo natural, você pode encontrar outras constantes matemáticas. Por exemplo, o número e , a base do logaritmo natural. Essa constante está incluída na fórmula da distribuição de probabilidade normal, que é dada pela função de densidade de probabilidade: A



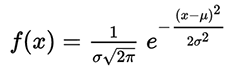distribuição normal está sujeita a muitos fenômenos naturais, incluindo muitas características de organismos vivos em uma população. Por exemplo, a distribuição de tamanhos de organismos em uma população: comprimento, altura, superfície, peso, pressão arterial em humanos e muito mais.

Uma observação cuidadosa do mundo à nossa volta mostra que a matemática não é uma ciência abstrata seca, como pode parecer à primeira vista. Muito pelo contrário. A matemática é a base de todo o mundo vivo e não vivo ao redor. Como Galileu Galilei observou corretamente, a matemática é a linguagem que a natureza nos fala.

Source: https://habr.com/ru/post/pt398987/