Calculadora de papelão e bola de quatro bits
Aparência de uma calculadora de papelão de quatro bits. O meio-somador acima e três somadores na parte central e inferior da calculadora são claramente visíveis.Umavez, antes da invenção da eletrônica, as pessoas faziam computadores mecânicos a partir de materiais improvisados. O exemplo mais famoso e complexo de tal máquina é o mecanismo antikythera - um dispositivo complexo de pelo menos 30 marchas foi usado para calcular o movimento dos corpos celestes e tornou possível descobrir a data de 42 eventos astronômicos.Atualmente, os computadores mecânicos (calculadoras) são mais um objeto de entretenimento para os geeks e uma ocasião para organizar um show engraçado. Por exemplo, como um computador de 10.000 blocos de dominó que soma números binários arbitrários de quatro dígitos e produz uma soma de dois dígitos de cinco dígitos (teoria matemática desta calculadora e arquitetura ). Tais performances permitem que as crianças entendam melhor como as operações lógicas de bits na programação funcionam e como as portas lógicas são organizadas. E, em geral, é muito interessante criar um computador pequeno com suas próprias mãos a partir de materiais improvisados, especialmente se você o fizer com seu filho.
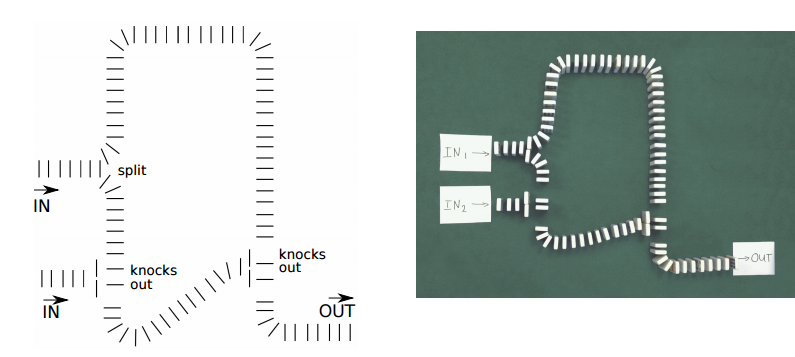A operação lógica e em um computador de 10.000 peças de dominó.Paraa fabricação de uma calculadora mecânica, o construtor Lego é excelente. Você pode encontrar muitos exemplos dessas calculadoras no YouTube .Calculadora de computador legoInspirado no exemplo de um computador feito de dominó e calculadoras mecânicas do construtor Lego, o programador C ++ sob o apelido lapinozz, junto com suas irmãs mais novas, decidiu construir em casa algo semelhante para um dos projetos científicos da escola da irmã. Ele concebeu e implementou uma calculadora LOGIC de quatro bits totalmente funcional (Logic cardbOard Gates Inpredictable Calculator) . Para produzir este computador, nada é necessário, exceto papelão e cola, e ele não funciona com eletricidade, mas com bolas e gravidade da terra. A calculadora pode adicionar números de 0 a 15, com no máximo 30.Ao contrário das peças de dominó e tijolos de Lego, nenhum componente de fábrica foi usado na fabricação desta calculadora. Todos os elementos da calculadora são colados a partir do papelão do zero, o que é bem compreendido pelas fotos do dispositivo. Nesse sentido, esse dispositivo pode ser considerado único.Objetivo do projeto
Representação visual de como adicionar números binários. Ensine um aluno a traduzir de decimal para binário e vice-versa. Estudo de operações lógicas de bits e circuitos lógicos básicos.Aparência da calculadora
Como você pode ver na fotografia da calculadora, na parte superior há uma zona para inserir dados. Depois de concluir todas as operações lógicas, as bolas mostram o resultado da operação abaixo.
A entrada de dados é realizada por bolas. A bola é - 1, a bola não é - 0. A parte da direita é a menor parte do número. Antes de iniciar o trabalho, algumas partes da calculadora devem ser colocadas em sua posição original. Depois de especificar os valores iniciais, a tira de papelão é empurrada para trás, que mantém as bolas na posição inicial - e o processo de adição é iniciado.Por exemplo, esta é a posição inicial das bolas para a operação 7 + 5 (0111 + 0101).
Dispositivo de calculadora
As operações lógicas de uma calculadora de papelão são realizadas de maneira semelhante, como no computador dominó acima mencionado .Portas lógicas esquemáticas para todas as operações lógicas são mostradas no diagrama.
Ou seja, a porta lógica "AND" (AND) significa que quando 0 bolas são recebidas na entrada, 0 na saída é obtido. Após o recebimento de 1 bola na entrada, 0 é obtido na saída. Após o recebimento de 2 bolas na entrada, 1 na saída é obtido.1 na entrada, 0 na saída
2 na entrada, 1 na saída
O portão lógico do XOR é um pouco mais complicado. Nesse caso, se uma bola chegar, ela deve passar. E se duas bolas chegarem, elas deverão se cancelar, ou seja, a saída será 0. O autor mostra como fazer isso, através de um pedaço de papelão pendurado verticalmente com um pescoço estreito. Se duas bolas chegam ao mesmo tempo, elas se bloqueiam - e, assim, implementam efetivamente a operação lógica do XOR.Porta lógica XOR
Para otimizar o sistema e não bloquear a massa das portas lógicas AND e XOR, o autor implementou um meio adicionador- um circuito lógico combinacional com duas entradas e duas saídas. O meio adicionador permite calcular a soma de A + B, com o resultado sendo dois bits S e C, onde S é o bit do módulo de soma 2 e C é o bit de transporte. Em nossa construção de papelão, isso significa que, se tivermos 1 bola na entrada, ela sairá C, e se houver 2 bolas na entrada, 1 bola sairá S e a segunda não chegará a lugar algum.O programador criou um esquema bastante simples e eficaz para um meio adicionador. Nela, uma bola na entrada continua calmamente seu caminho, girando a barreira e passando para o buraco C. Mas se duas bolas entrarem, a segunda bola não poderá mais passar através da barreira, virada pela primeira bola - e cair no buraco, pregando um novo caminho S. Este é um meio-adicionador.Uma bola na entrada do semi-somador
Duas bolas na entrada do meio adicionador
Finalmente, o adicionador é uma verdadeira obra-prima. Geralmente, ele é composto de dois semi-adicionadores e um portão lógico “OR”, mas o autor implementou outro design, que na verdade é uma pequena modificação do semi-somador.Uma bola na entrada - uma bola no caminho 1
Duas bolas na entrada - uma bola no caminho 2
Três bolas na entrada - uma bola no caminho 1 e a outra ao longo do caminho 2
Toda a calculadora consiste inteiramente em um meio-somador e três somadores.
A calculadora fornece o resultado correto do cálculo se as bolas caírem na velocidade correta, nem muito rápidas nem muito lentas, e não saltam uma da outra. A lógica em si é impecável, mas, na prática, a calculadora às vezes é incorreta.Source: https://habr.com/ru/post/pt399391/
All Articles