Estruturas misteriosas combinam matemática e natureza

Na cidade de Cuernavaca, no México, uma rede de "espiões" aumenta a eficiência da frota de ônibus. Como resultado, o horário de partida do ônibus sempre corresponde ao padrão de "universalidade"

Em 1999, sentado em um ponto de ônibus em Cuernavaca, México, o físico tcheco Petr Šeba notou pessoas dando pedaços de papel aos motoristas em troca de dinheiro. Ele descobriu que isso não era uma manifestação do crime organizado, mas um comércio “sombra” diferente: cada motorista pagava um “espião”, observando quando o ônibus anterior saiu do ponto de ônibus. Se ele partisse recentemente, o motorista desse ônibus diminuiu a velocidade para que os passageiros pudessem se reunir na próxima parada. Se esse ônibus partisse há muito tempo, o motorista acelerava para que outros ônibus não o ultrapassassem. Esse sistema maximizava os lucros dos motoristas. O que deu uma ideia a Sheba.

"Pensamos que estávamos observando uma situação que lembra um pouco os sistemas quânticos caóticos", explicou o co-autor de Sheba, Milan Krbálek.

Após várias tentativas frustradas de se comunicar com os "espiões", Sheba pediu ao aluno que explicasse que ele não era do imposto ou da máfia. Ele é apenas um cientista louco que muda a tequila para os dados deles. E as pessoas lhe deram suas anotações. Quando os pesquisadores traçaram milhares de horários de partida de ônibus, suas suspeitas foram confirmadas. A interação entre os motoristas levou à distribuição de lacunas entre os resíduos de transporte, o que coincidiu com a estrutura de alguns experimentos em física quântica.

"Eu estava pensando que algo assim poderia aparecer, mas fiquei surpreso ao ver uma coincidência exata", disse Sheba.

Partículas subatômicas têm pouco em comum com um sistema de ônibus descentralizado. Mas, ao longo dos anos desde a descoberta de interações quânticas estranhas, as mesmas estruturas de dados apareceram em outras situações não relacionadas. Os cientistas acreditam que esse fenômeno comum, conhecido como "universalidade", é devido à conexão matemática dos fenômenos e os ajuda a simular sistemas complexos, da Internet ao clima do planeta.


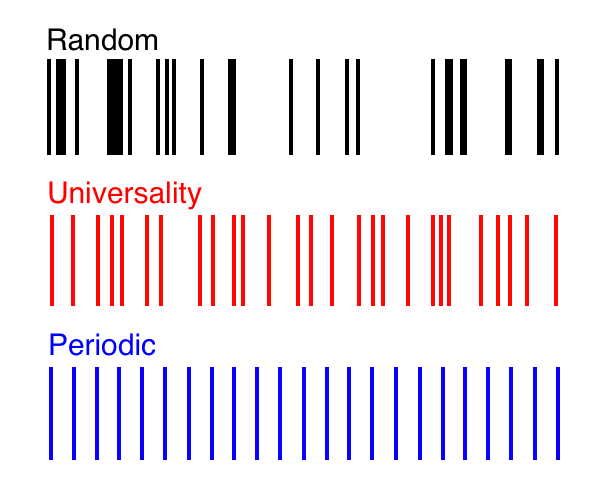O gráfico vermelho representa o equilíbrio perfeito entre aleatoriedade e periodicidade, conhecido como universalidade. É observado nos espectros de muitos sistemas complexos com correlação. Nesse espectro, a função de correlação matemática fornece a probabilidade exata da presença de duas linhas a uma determinada distância uma da

outra.Esta estrutura foi encontrada pela primeira vez na natureza na década de 1950 emespectro de energia de um núcleo de urânio , um monstro com centenas de partes móveis, oscilando e se estendendo de inúmeras formas e dando uma sequência infinita de níveis de energia. Em 1972, Hugh Montgomery, especialista em teoria dos números, observou-o nos zeros da função zie de Riemann , um objeto matemático relacionado à distribuição dos números primos. Em 2000, Krbalek e Sheba a encontraram em um horário de partida de ônibus em Cuernavaca . E, recentemente, apareceu nas medições espectrais de materiais compósitos, como gelo marinho e tecido ósseo humano, e na dinâmica dos sinais do modelo Erd-s-Reni , uma versão simplificada da Internet.

Cada um desses sistemas possui um espectro - uma sequência de código de barras que representa dados como níveis de energia, zeta zeros, horário de partida do ônibus ou velocidade do sinal. Estruturas idênticas aparecem em todo o espectro. A distribuição dos dados parece aleatória, mas, ao mesmo tempo, as linhas adjacentes se "repelem", o que leva a uma certa regularidade das lacunas. O equilíbrio exato entre caos e ordem, determinado pela fórmula, também aparece em problemas puramente matemáticos: determina a distância entre os valores próprios de uma matriz preenchida com números aleatórios.

"Por que tantos sistemas físicos se comportam como matrizes aleatórias permanece um mistério", diz Horng Tzer Yao, matemático da Universidade de Harvard. "Mas nos últimos três anos, demos um passo muito importante para entender isso".

Para estudar o fenômeno da universalidade em matrizes aleatórias, os cientistas entendem um pouco por que ele aparece em toda parte e como pode ser usado. Em uma pilha de novos artigos, Yao e outros matemáticos descreveram muitos novos tipos de matrizes aleatórias que obedecem a várias distribuições numéricas e regras de simetria. Por exemplo, os números para colunas e linhas de matrizes podem ser obtidos da curva de distribuição normal dos valores possíveis, ou você pode preenchê-lo com os valores 1 e -1. As partes superior direita e inferior esquerda da matriz podem se espelhar ou não serem exibidas. E, independentemente de suas características, as matrizes aleatórias exibem os mesmos espectros caóticos, mas regulares, na distribuição de seus valores próprios. Portanto, os matemáticos chamavam esse fenômeno de "universalidade".

"Parece uma lei da natureza", diz Wang Wu, matemático da Universidade de Yale, que, junto com Terence Tao da Universidade da Califórnia em Los Angeles, provou universalidade para uma ampla classe de matrizes aleatórias.

Acredita-se que a universalidade apareça em sistemas muito complexos, consistindo de muitas partes que interagem intimamente entre si para criar um espectro. Uma configuração aparece no espectro de uma matriz aleatória, por exemplo, porque todos os elementos da matriz são usados ​​no cálculo desse espectro. Mas matrizes aleatórias, de acordo com Wu, são simplesmente "sistemas de brinquedos", são simples o suficiente para aprender e ricas o suficiente para modelar sistemas reais. Versatilidade é muito mais comum. A hipótese de Wigner (nomeada em homenagem a Eugene Wigner, a phisis que descobriu a universalidade no espectro dos átomos), sugere que todos os sistemas complexos com correlação são universais, da estrutura cristalina à Internet.

Quanto mais complexo o sistema, mais universal ele se manifesta, diz Laszlo Erdös, da Universidade de Munique, um dos colegas de trabalho de Yao. "Você acredita que a universalidade é um comportamento típico."

Em muitos sistemas simples, os componentes individuais podem influenciar demais o resultado geral, o que altera a aparência do espectro. Sistemas maiores não têm domínio de componente único. "Acontece que há uma sala com muitas pessoas decidindo fazer algo, e a identidade de uma delas não é tão importante", diz Wu.


Os matemáticos usam matrizes aleatórias para estudar e prever algumas propriedades da Internet, por exemplo, o tamanho de um cluster de computador típico

Quando um sistema demonstra universalidade, isso serve como garantia de que é complexo e existe correlação suficiente dentro dele para ser interpretado como uma matriz aleatória. "Isso significa que você pode usar uma matriz aleatória para modelá-la", diz Wu. "Você pode calcular outros parâmetros do modelo com base na matriz e usá-los para prever o comportamento deste sistema."

Essa técnica permite que os cientistas entendam a estrutura e evolução da Internet. Algumas propriedades dessa enorme rede de computadores, como o tamanho típico de um cluster de computadores, podem ser estimadas com bastante precisão através das propriedades medidas da matriz aleatória correspondente. "As pessoas estão interessadas em grupos e sua localização, e isso geralmente ocorre devido a objetivos práticos, como publicidade", diz Wu.

Tecnologias semelhantes podem levar a melhorias nos modelos de mudança climática. Os cientistas descobriram que a presença de universalidade, semelhante ao espectro de energia, no material indica uma forte conexão de suas partes e, como resultado, boa condutividade de líquidos, eletricidade ou calor. E vice-versa, a falta de versatilidade pode indicar escassez do material e suas propriedades isolantes. Em um novo artigo apresentado em uma conferência matemática em San Diego, Ken Golden, matemático da Universidade de Utah, e seu aluno Ben Murphy, usaram essa diferença para prever a condutividade térmica e os fluxos de fluido no gelo do mar, tanto no nível microscópico quanto no Absinto do Ártico, presente em territórios que se estendem por milhares de quilômetros.

Uma medição espectral do mosaico de absinto derretido fotografado em um helicóptero, ou dados de gelo marinho obtidos de uma amostra, mostram o estado de cada um desses sistemas. "O fluxo de fluido através do gelo marinho conduz processos muito importantes que precisam ser entendidos para entender o sistema climático", diz Golden. "As transições nas estatísticas de nossas próprias decisões representam uma nova abordagem matematicamente rigorosa para a inclusão do gelo do mar nos modelos climáticos".

O mesmo truque pode levar a um teste simples para osteoporose. Golden, Murphy e seus colegas descobriram que o espectro de um osso denso e saudável tem versatilidade, enquanto o espectro de um osso poroso não.


Os absinto do Ártico são universais se estiverem suficientemente conectados

"Trabalhamos com sistemas cujas" partículas "podem ter milímetros ou quilômetros de tamanho, diz Murphy sobre os componentes do sistema. "É incrível que a mesma matemática descreva todos eles."

A razão pela qual sistemas reais exibem comportamento semelhante a uma matriz aleatória talvez seja mais fácil de entender no caso de um núcleo de átomos pesados. Todos os sistemas quânticos, incluindo átomos, funcionam de acordo com as regras da matemática, especialmente com a participação de matrizes. "Essa é a essência da mecânica quântica", diz Freeman Dyson, um ex-físico matemático que ajudou a desenvolver a teoria das matrizes aleatórias nas décadas de 1960 e 1970 no Instituto de Engenharia Avançada de Princeton. "Cada sistema quântico é descrito por uma matriz que representa sua energia total e as próprias soluções da matriz são os níveis de energia do sistema quântico".

As matrizes de átomos simples, hidrogênio e hélio, podem ser calculadas exatamente, e as soluções de eigen obtidas coincidem com uma precisão surpreendente com os níveis de energia medidos dos átomos. Mas as matrizes de sistemas mais complexos, como o núcleo de urânio, tornam-se muito "espinhosas" para "agarrá-las". Segundo Dyson, por causa disso, esses núcleos podem ser comparados com uma matriz aleatória. Muitas interações no urânio - elementos de uma matriz desconhecida - são tão complexas que sua mistura produz ruído, como muitos sons sobrepostos. Como resultado, a matriz desconhecida que controla o núcleo se comporta como uma matriz com números aleatórios e seu espectro é universal.


Tais, absinto desconectado, não têm universalidade, seu espectro é aleatório

Os cientistas ainda não desenvolveram uma compreensão intuitiva de por que sistemas complexos demonstram essa e não outra sequência aleatória / periódica. "Só sabemos disso pelos cálculos", diz Wu. Outro mistério é sua conexão com a função zeta de Riemann, na qual a universalidade se manifesta no espectro de zeros. Esses zeros estão intimamente relacionados à distribuição dos números primos - os números inteiros irredutíveis que compõem o resto. Os matemáticos há muito procuram uma descrição da distribuição dos números primos em uma linha numérica de 1 ao infinito, e a universalidade lhes dá a chave. Alguns acreditam que uma função zeta de Riemann pode ser matriculada suficientemente complexa e coerente para possuir universalidade. A descoberta dessa matriz teria uma "forte influência" no entendimento da distribuição dos números primos, como disse Paul Bourgade, um matemático de Harvard.

É possível que a explicação esteja oculta ainda mais. "Pode acontecer que no centro da universalidade e função zeta de Wigner não esteja a matriz, mas alguma estrutura matemática que ainda não foi descoberta", diz Erdös. "Matrizes Wigner e funções zeta podem ser diferentes representações dessa estrutura."

Muitos matemáticos estão procurando uma resposta sem garantia de uma. “Ninguém imaginou que os ônibus em Cuernavac seriam um exemplo. Ninguém imaginou que zeros da função zeta seriam outro exemplo, diz Dyson. "A beleza da ciência é sua imprevisibilidade, e tudo o que é útil vem de surpresas."

Source: https://habr.com/ru/post/pt399535/