Especialistas em TI andam em estradas não pavimentadas
Após décadas de estagnação, novos atalhos foram encontrados para o problema do vendedor ambulante.
Há pouco tempo, uma equipe de pesquisadores da Universidade de Stanford e McGill quebrou o recorde de 35 anos em ciência da computação em uma quantidade inimaginavelmente pequena - em quatrocentos de um trilionésimo trilionésimo trilionésimo por cento. O avanço - um problema de vendedor criado no problema dos clássicos da ciência da computação - era pequeno demais para qualquer valor prático, mas ele deu uma nova vida em busca de soluções aproximadas aprimoradas.A tarefa é formada da seguinte forma: para um conjunto de cidades conectadas por estradas, é necessário encontrar o caminho mais curto para visitar cada cidade com retorno ao ponto de partida. As soluções para o problema têm aplicações práticas, desde a abertura de furos em placas de circuito impresso até o gerenciamento da programação de tarefas em um computador e a organização das propriedades do genoma.O problema do vendedor é fácil de formular e - em teoria - fácil de resolver, verificando todos os caminhos fechados possíveis para encontrar o mais curto. O problema com a abordagem da força bruta é que, quando o número de cidades cresce, o número correspondente de caminhos começa muito rapidamente a exceder as capacidades dos computadores mais rápidos. Para dez cidades, existem mais de 300.000 rotas. Para 15 cidades, seu número sobe para 87 bilhões.Algoritmo Christofides
No início da era dos computadores, os matemáticos esperavam que alguém encontrasse uma abordagem conveniente para o problema - um algoritmo que permite que ele seja resolvido em um tempo razoável. Mas, embora os programadores tenham progredido em casos específicos - determinando o caminho mais curto para 49 cidades na década de 1950, para 2.392 cidades na década de 1980 e para 85.900 cidades em 2006 - ninguém propôs um algoritmo que resolva efetivamente o problema no caso geral. De acordo com o notável trabalho de 1972, é possível que esse algoritmo não exista. O cientista da computação Richard Karp, da Universidade da Califórnia em Berkeley, mostrou que o problema do vendedor é NP-completo, o que significa que não há algoritmo eficiente (a menos que alguém prove que P = NP - mas a maioria dos cientistas acredita que isso não é assim). .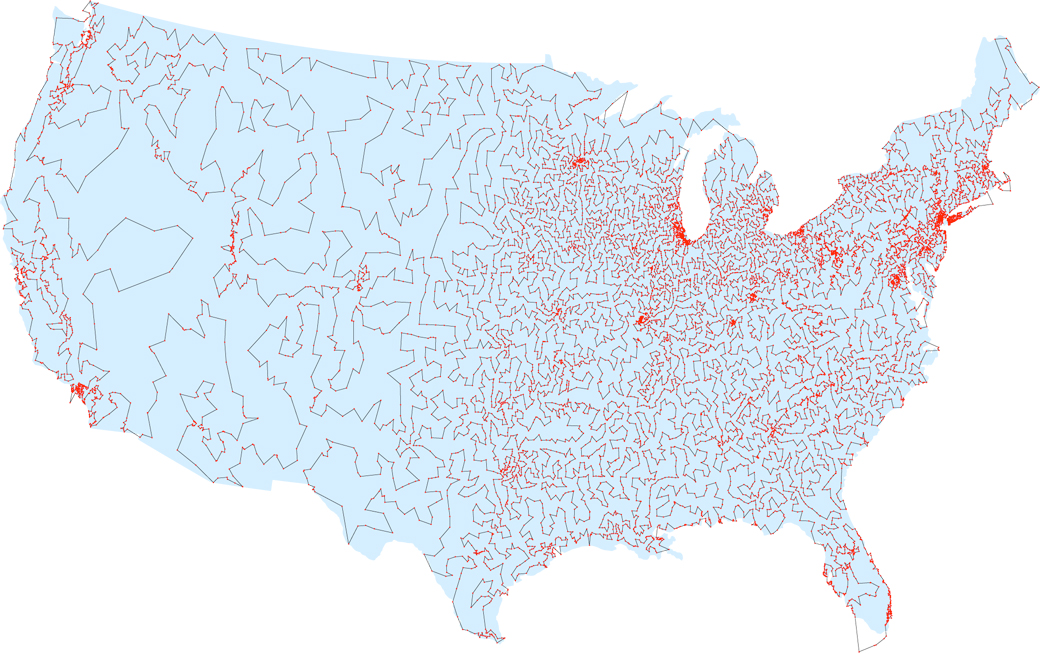
A rota mais curta por todas as 13.509 cidades nos Estados Unidos, com uma população de mais de 500 (segundo dados de 1998)Após a publicação de Karp, muitos cientistas da computação começaram a desenvolver um algoritmo eficaz para encontrar soluções aproximadas para o problema - caminhos fechados cujo comprimento é apenas ligeiramente maior que o menor. E aqui eles tiveram mais sorte - em 1976, Nikos Christofides, professor do Imperial College de Londres, desenvolveu um algoritmo que produz caminhos que garantem não exceder o caminho mais curto em mais de 50%.Após sua criação, muitos cientistas decidiram que esse algoritmo, que é simples o suficiente para os alunos estudarem em uma hora, se tornará um elo intermediário, após o qual será encontrada uma solução verdadeira mais complexa e com melhor aproximação. Mas décadas depois, esses algoritmos nunca apareceram."Quase todos os estudantes de ciência da computação passaram semanas ou meses tentando melhorar o algoritmo de Christofides", disse Sanjeev Arora, cientista da Universidade de Princeton.Finalmente, em 2011, a equipe de Stanford e McGill superou a garantia de 50% para certos tipos de tarefas de vendedor e mostrou que suas soluções excederiam o caminho mais curto em não mais do que 49.99999999999999999999999999999999999999999999999999696%.Desde então, surgiram vários algoritmos aproximados aprimorados, graças a uma nova visão do problema. Embora essas aproximações se apliquem apenas a certos tipos de tarefas de vendedores ambulantes, sua abordagem é bastante promissora, de acordo com Michel Goemans, especialista em TI do Instituto de Tecnologia de Massachusetts."Nós apenas tocamos a superfície um pouco", diz ele. "Acredito que talvez em cinco anos alcançaremos resultados mais impressionantes".Árvore mais curta
Mona Lisa como um caminho entre 100.000 cidadesO algoritmo Christofides não começa com uma busca pelo caminho mais curto, mas com uma busca por uma árvore de abrangência mínima - um conjunto de ramificações que conectam cidades sem loops fechados. Ao contrário do caminho mais curto, a árvore de extensão mínima é bastante fácil de construir - você precisa começar procurando o caminho mais curto entre as duas cidades; este será o primeiro ramo. Para adicionar o seguinte, você precisa encontrar o caminho mais curto entre a nova cidade e uma das duas anteriores - e assim por diante, até que todas as cidades sejam cobertas.A árvore resultante não é uma das soluções possíveis para o problema do vendedor ambulante, pois não nos fornece um caminho fechado. Mas pode ser transformado em um caminho assim, imaginando que os galhos são paredes e depois caminhando ao longo da árvore para que seu dedo toque a parede até você chegar ao começo. A caminhada resultante passa por cada cidade e retorna, mas geralmente está longe do caminho mais curto, pois passa muitas vezes pelos mesmos segmentos - caminhamos cada parede em uma árvore duas vezes, uma de cada lado.Mas o caminho resultante, na pior das hipóteses, não é mais do que o caminho mais curto duas vezes. Ao adicionar ramificações especialmente selecionadas e aplicar alguns truques, a Christofides mostrou como cortar esse caminho para que não exceda o mais curto em mais de 50%.Uma árvore de abrangência mínima é um ponto de partida natural para criar uma solução alternativa curta. Mas essa abordagem também serviu como ponto de partida para os pesquisadores que tentam obter uma garantia de 50% da Christofides. Afinal, embora uma árvore de abrangência mínima pareça eficaz a princípio, outras árvores podem ser mais adequadas para o processo de conversão de árvores em uma solução alternativa - por exemplo, você precisa adicionar apenas uma perna a uma árvore sem ramificação, para que ela se torne uma solução alternativa.Portanto, o objetivo era encontrar uma árvore que alcance um equilíbrio entre comprimento e conversão simples em uma solução alternativa. Não há algoritmos eficazes para procurar uma árvore ideal (se P = NP não for verdadeiro), mas um algoritmo aproximado bem-sucedido precisa encontrar apenas o suficiente.Viagem fracionária
O caminho para uma árvore "razoavelmente boa" incluía uma técnica popular, embora contra-intuitiva, que reconhecia soluções fracionárias para tarefas específicas. Por exemplo, uma solução alternativa fracionária pode incluir viagens a meio caminho entre Minneapolis e Detroit e a meio caminho entre Cleveland e Detroit. Do ponto de vista prático, esse caminho não faz sentido. Mas pode ser descrito com precisão matematicamente e, diferentemente do problema clássico do vendedor ambulante, uma versão fracionária pode ser resolvida com eficiência.Muitos problemas de aproximação na ciência da computação podem ser resolvidos calculando soluções para a versão fracionária do problema e, em seguida, arredondando inteligentemente os compartilhamentos para obter uma solução aproximada para o problema original. Mas até recentemente, ninguém ainda havia descoberto como fazer isso no caso do problema do vendedor ambulante.Em 2009, Amin Saberi, da Universidade de Stanford, e Arash Asadpour, então estudante de pós-graduação, desenvolveram um esquema geral de arredondamento que usa números aleatórios para selecionar uma solução inteira que preserva o máximo possível de propriedades da solução fracionária. Saberi acreditava que esse padrão lembrava um "martelo pesado em busca de um prego". E ele suspeitava que a tarefa do vendedor pudesse ser a unha certa.Poucos meses depois, Sabre, Asadpur, Gomans, Shayan Gharan e Aleksander Madry, estudante de Stanford, agora trabalhando na Escola Politécnica Federal de Lausanne, na Suíça, mostraram que a nova técnica de arredondamento pode fornecer um bom algoritmo aproximado para uma das opções. tarefas do vendedor, o caso "assimétrico". Um ano depois, Saberi, Garan e Mohit Singh, da McGill University, usaram a mesma abordagem para desenvolver um novo algoritmo aproximado para o problema usual dos vendedores ambulantes.
O maior problema de vendedores ambulantes solicitados foi o caminho entre 85.900 cidades, calculado em 2006. A localização das “cidades” corresponde ao design de um chip de computador específico criado no laboratório de Bell, e a solução é a maneira mais curta para o corte a laser.Tendo recebido um mapa de cidades e rotas, o novo algoritmo começa calculando a solução fracionária exata do problema do vendedor ambulante. Ele então arredonda essa solução para uma árvore de abrangência, que teoricamente deve chegar perto de um equilíbrio entre comprimento e conversão simples em uma solução alternativa. Finalmente, o algoritmo inclui essa árvore - e não a árvore de abrangência mínima - na rede Christofides.O novo algoritmo era "uma idéia que poderíamos explicar em algumas horas, mas sua prova levou cerca de um ano", diz Saberi.Após uma longa análise, a equipe de Stanford / McGill conseguiu melhorar o algoritmo de Christofides em uma pequena fração para uma ampla subclasse de tarefas de vendedor, “gráfica”. Alguns meses depois, outras equipes, inspiradas pelo sucesso, usaram outros esquemas de arredondamento para obter algoritmos para o caso gráfico com melhores aproximações. O recorde atual é de 40%, o que é muito melhor do que 50% do Christofides.O estojo gráfico "inclui muitas das mesmas dificuldades encontradas no problema geral", diz Arora, acrescentando que os esquemas que funcionam no estojo gráfico também podem ser úteis para o problema geral dos vendedores ambulantes.No entanto, diz Saber, a solução do problema geral aproximado do vendedor provavelmente exigirá novas idéias. “Uma descoberta matemática é como se mudar para um quarto escuro. Você alcança e encontra uma cadeira, alcança e encontra uma mesa ”, diz ele, parafraseando o matemático Andrew Wiles. “Em algum momento, a mão encontra um interruptor e, de repente, tudo fica claro. No caso da tarefa do vendedor, mesmo depois de tantos trabalhos que encontraram tantos limites possíveis, não me parece que já tenhamos encontrado essa opção ".Source: https://habr.com/ru/post/pt399873/
All Articles