(continuação. Parte anterior: “Automação a partir de DNA e proteínas: o que isso tem em comum com a eletrônica?” )Decidimos que o operon lactose é semelhante ao elemento lógico AND. Mas de onde vêm suas propriedades digitais? Afinal, ambos os sinais de entrada (concentrações de cAMP e lactose) são, de fato, analógicos. Vamos tentar desenhar as funções de entrada do operon lactose.Cada entrada do repressor de lactose consiste em dois estágios de reconhecimento molecular. A lactose se liga ao repressor de lactose e o repressor se liga ao DNA. Existem várias dezenas de moléculas repressoras na célula, cada uma das quais, desde que não exista lactose, pode se ligar ao início do operon da lactose. Quando está ligada, a RNA polimerase não pode começar a trabalhar. Devido ao movimento térmico da molécula repressora, ela continua caindo do DNA e ligada novamente. Se não houver nenhum repressor, o operon opera com força total (agora, por simplicidade, consideramos que há um excesso de ativador catabólico). Em baixas concentrações do repressor, reduz a atividade do operon quase linearmente. Mas então o efeito de cada nova parte do repressor é cada vez menor e, em geral, o gráfico de dependência está próximo da hipérbole y = 1 / (x + 1)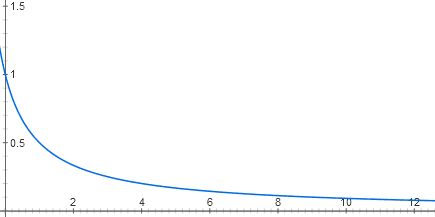
matan. . ?
, , . , :
A + B <-> C
, , - . , - ( , [A], [B] [C] ). : , , .
[C] / ([A] * [B]) = K
. (. . ) . , , .
, , , , ( ) . [C] ([A] * [B]) .
, : RepA + OpA <-> Op ( ). {R-O} = [Op] / ([OpA] * [RepA]). [] ( ) [RepA] ( ). , , : [Op] + [OpA] = 1
[Op] [OpA] :
{R-O} = (1 — [OpA]) / ([OpA] * [RepA])
:
[OpA] = 1 / (K{R-O} * [RepA] + 1)
y = 1 / (x + 1)
As moléculas repressoras flutuam na célula e se ligam ao DNA apenas em pacotes de quatro. Para que a forma ativa do repressor se torne inativa, ela deve se ligar a quatro moléculas de lactose - uma ou duas não é suficiente, você precisa de uma molécula de lactose para cada subunidade proteica do repressor quad. Embora haja pouca lactose na célula, suas moléculas se ligam ao repressor um ou dois e permanece ativo. Porém, após uma certa concentração limiar de lactose, a maioria das moléculas repressoras liga quatro moléculas de lactose e passa para uma forma inativa. O gráfico da atividade do repressor, dependendo da quantidade de lactose, tem, portanto, uma forma de S e é descrito por uma função da forma y = 1 / (1 + x ^ 4).Matan[RepA] [Lac]. , : .
RepA + 4 Lac <-> Rep
:
{R-L} = [Rep] / ([RepA] * [Lac]^4)
, :
[Rep] + [RepA] = n, n ≈ 50
, [RepA] = n / ({R-L} * [Lac]^4 + 1)
Agora, para obter a característica de entrada do operon para lactose, é necessário substituir a segunda função na primeira. Ele terá a forma, até os coeficientes,y = 1 / (1 + (1 / (1 + x ^ 4))))Sua agenda também é em forma de S. Acontece que o operon lactose não responde a baixas concentrações de lactose. Quando a concentração limiar é atingida, aparecem moléculas repressoras inativas que se ligam a quatro lactoses cada, e o operon liga bastante bruscamente.A segunda entrada reguladora do operon lactose também consiste em duas etapas de reconhecimento molecular: o cAMP se liga ao ativador e o ativador ao DNA. A diferença da entrada de lactose é que aqui a ligação de moléculas (ativador ou cAMP) aumenta a atividade do que eles entraram em contato (operon ou ativador). Ou seja, os gráficos vão do zero e se aproximam da linha horizontal em algum lugar acima do eixo X.Matan, , :
2 + Akt <-> AktA
K{-} = [AktA] / ([Akt] * []^2)
, [AktA] [Akt] , 100 , . [Akt] [AktA], :
K{-} = [AktA] / ((100 — [AktA]) * []^2)
[AktA] = K{-} * []^2 / (1 + K{-} * []^2)
[AktA] [] y = x^2 / (1 + x^2)
Devido à ligação de duas moléculas de cAMP, o gráfico não se parece com uma hipérbole, mas como uma curva em forma de S. Embora o efeito limite seja menos perceptível do que no gráfico da lactose, porque o grau não é o quarto, mas apenas o segundo.A dependência da atividade do operon na quantidade de ativador tem uma nuance diferente. Se a ligação do repressor suprime quase completamente o operon (em algum lugar até 0,1%, que é menor que o erro de medição bioquímico), a ausência de ativador suprime a atividade apenas em até 5%. Portanto, o gráfico sairá não do zero, mas do ponto (0; 0,05):y = 0,05 + (0,95 * x / (1 + x))Matan« , » ,
= [OpA] + 0,05 * [Op]
[OpA] [AktA] . , , [AktA] . , , [AktA] , :
[OpA] = K{-O} * [AktA] / (K{-O} * [AktA] + 1)
y = x / (1 + x)
, ! , (1 — ) * 0,05. , , :
y = 0,05 + (0,95 * x / (1 + x))
Resta obter a dependência da atividade do operon na concentração de cAMP. Para fazer isso, substitua a primeira fórmula (para a concentração da CAP ativa, dependendo da concentração de cAMP) na segunda fórmula (para a atividade do operon a partir da concentração da ATS ativa) ...... E obtenha uma fração de quatro andares:Temos a função mais complexa de todas neste artigo. No entanto, seu gráfico se parece com um gráfico de uma dependência mais simples da CAP ativa na concentração de cAMP, y = x ^ 2 / (1 + x ^ 2):É também uma curva em forma de S com algum efeito limiar, que se aproxima lentamente da horizontal y = 1. Começa não apenas a partir do zero, mas a partir do ponto (0; 0,05).Resta entender como as duas entradas interagem. No caso do operon lactose, a resposta é simples - nada. O repressor da lactose e o ativador catabólico não afetam a ligação um do outro ao DNA. Portanto, a ligação dessas duas proteínas pode ser considerada um evento independente. A atividade completa do operon é alcançada quando o ativador está conectado e o repressor não está conectado. A probabilidade de tal coincidência é igual ao produto das probabilidades de cada uma delas separadamente. Portanto, para obter a função de atividade do operon lactose a partir de duas variáveis ([Lac]) e ([cAMP]), basta multiplicar as funções de cada uma dessas variáveis:Atividade = (1 / (1 + (1 / (1 + [Lac] ^ 4))) * (0,05 + 0,095 * ([cAMP] ^ 2 / (1 + [cAMP] ^ 2)) / ( 1 + ([cAMP] ^ 2 / (1 + [cAMP] ^ 2))))Gráfico tridimensional desta funçãoParece um platô terminando em gargantas nos dois lados. O desfiladeiro direito (baixas concentrações de lactose) é mais profundo e de fundo plano do que o esquerdo (baixas concentrações de cAMP).Na vida real, E. coli ao seu redor ou não existe lactose (na maioria das vezes), ou sua concentração é superior ao limiar e o repressor de lactose praticamente não interfere na operação do operon (quando o proprietário comeu algo lácteo). A concentração de cAMP é um sinal interno produzido pela própria célula. Também é pequeno demais para incluir o operon da lactose (quando há glicose ou amido) ou o suficiente para ativar 95% ou mais (se não houver nada mais saboroso que a lactose). Ou seja, quase sempre o operon lactose está nas condições de um platô neste gráfico ou em um dos desfiladeiros.As funções de entrada do operon lactose são medidas experimentalmente. O método de medição se assemelha à técnica de depurar microcontroladores "pendure o LED na perna de saída". A região reguladora do operon é tomada e ligada ao gene da proteína verde fluorescente. Essa construção genética é inserida nas células de Escherichia coli, das quais o operon normal de lactose é removido (para que a concentração de lactose seja estritamente definida pelo pesquisador) e no sistema padrão que codifica a fome com níveis de AMPc. Depois disso, a atividade do operon lactose pode ser medida com precisão por um espectrofotômetro de acordo com o nível de fluorescência verde. Acontece que, dentro dos limites da precisão da medição (1%), a teoria converge completamente com o experimento ).A parte inferior do desfiladeiro esquerdo no gráfico da função de entrada (em baixas concentrações de cAMP) está acima de zero. Isso não é um bug, mas uma característica: graças a ele, na presença de vários açúcares ao mesmo tempo, a E. coli está pronta para mudar rapidamente para a lactose quando a glicose terminar. Os mutantes de Escherichia coli, nos quais a função reguladora do operon da lactose está mais próxima do AND puro (ou seja, o operon não funciona sem o cAMP), alternam de glicose para lactose por uma hora ou mais: no momento da exaustão da glicose, eles não possuem enzimas de captação de lactose, o que significa que não há energia para torná-los rapidamente. A Escherichia coli normal ("tipo selvagem") atende a esse ponto, já tendo algumas enzimas para a absorção de lactose e leva de 15 a 20 minutos para mudar completamente para um novo açúcar.Agora vamos desviar do operon da lactose e examinar de maneira mais ampla o que os elementos lógicos dessa base química são capazes. Em quase todos os lugares nos sistemas de sinalização bioquímica, encontramos reconhecimento molecular, que é descrito por funções da forma y = x ^ n / (1 + x ^ n) para ativadores e y = 1 / (1 + x ^ n) para repressores. O grau n nessas funções mostra o número de moléculas do mesmo tipo para se ligar para obter um efeito, e geralmente é igual a 1, 2 ou 4 (na maioria das vezes 2). Chaves lógicas mais complexas podem ser obtidas adicionando mais locais de ligação às proteínas reguladoras no início do operon. Pode haver mais de dois tipos dessas proteínas. Os efeitos de diferentes proteínas no desembarque da RNA polimerase podem somar (OR) ou multiplicar (AND).Mas, em geral, trataremos de alguma combinação (adição ou multiplicação) das funções básicas y = x ^ n / (1 + x ^ n) e y = 1 / (1 + x ^ n) com diferentes graus e coeficientes.Algumas características interessantes são muito simples. Por exemplo, a mesma proteína reguladora pode se ligar (em forma pareada) a duas regiões do promotor. Em uma seção, atua como repressor e em outra - como ativador. Para o operon funcionar, é necessário que o local do repressor esteja vazio e o local do ativador esteja ocupado. Acontece uma função com um máximo claro:y = (1 / (1 + x ^ 2)) * (x ^ 2 / (1 + x ^ 2))Sem essa proteína, o operon fica inativo porque o local do ativador está vazio e em altas concentrações é inativo porque o site está ocupado repressor. A atividade máxima será quando o local do ativador e o local do repressor estiverem ocupados com uma probabilidade de 50%.Você ainda pode criar dois locais de ligação do ativador, em um o ativador se ligará fortemente ao DNA, mas ativará fracamente o gene, no outro - se ligará levemente ao DNA, mas ativará fortemente o gene. Nesse caso, obtemos uma função como y = x ^ 4 / (1 + x ^ 4) + 0,3 * (10x) ^ 4 / (1 + (10x) ^ 4), com um gráfico passo a passo:Matemática, sim! Você pode dizer nos comentários o que mais é possível e o que não pode ser obtido adicionando e multiplicando essas funções básicas y = x ^ n / (1 + x ^ n) e y = 1 / (1 + x ^ n)?Na próxima parte, trataremos dos circuitos de tais elementos lógicos.