Não vou mentir, estou ansioso pelo filme Homem-Aranha: De Volta ao Lar [Homem-Aranha: De Volta ao Lar]. Enquanto isso, a única saída para mim será fazer a física do Homem-Aranha. E cuidarei de suas novas asas de teia de aranha vistas no último trailer.Para os fãs, notei que alguns dos quadrinhos originais sobre o Homem-Aranha realmente mostraram como ele os usa, embora ele nem sempre os usasse para voar.Planejamento físico
O que acontece depois que o Homem-Aranha pula de um prédio? Posso simular seu movimento aceitando que três forças agem sobre ele - gravidade, resistência do ar e sustentação. Com sua permissão, descreverei cada um deles.• Gravidade - uma força descendente constante proporcional à massa da emergência (pelo menos na superfície da Terra).• resistência. Imagine que você está puxando um objeto através de um gigantesco mar de bolas de pingue-pongue. Substitua as bolas por ar - e será a mesma coisa. A resistência aumenta com a velocidade.• Força de elevação. Mais uma vez, imagine colisões com bolas, mas depois disso as bolas saltam para baixo. Substituindo as bolas pelo ar, você receberá uma carona, dependendo do ângulo de ataque, superfície e velocidade.Aqui está um belo diagrama das forças de uma pessoa que planeja asas de emergência. Sim, enquanto o modelamos com um triângulo.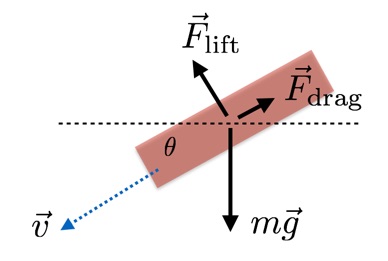 Em nosso modelo simples, a força de elevação é perpendicular à velocidade e a resistência é direcionada na direção oposta. Para simular o movimento de uma emergência com asas, preciso de uma fórmula para os dois.
Em nosso modelo simples, a força de elevação é perpendicular à velocidade e a resistência é direcionada na direção oposta. Para simular o movimento de uma emergência com asas, preciso de uma fórmula para os dois.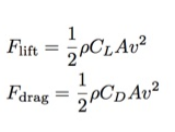 Estes são valores de forças que são importantes para nós. Eles são semelhantes, com exceção de C L (coeficiente de elevação) e C D (coeficiente de arrasto). Nos dois casos, ρ é a densidade do ar (1,2 kg / m 3 ) e v é a velocidade.O que é um? Esta é a área transversal de uma pessoa (emergência no nosso caso). Em teoria, A para resistência e força de elevação deve diferir, dependendo do ângulo de ataque. Mas nem sempre sei exatamente o que estou fazendo - é por isso que verifiquei com fontes diferentes e o artigo de 2011 “ A trajetória de um Batman em queda"da revista física Journal of Physics Special Topics. Nela, os autores usaram a mesma área para resistência e sustentação, então farei o mesmo.
Estes são valores de forças que são importantes para nós. Eles são semelhantes, com exceção de C L (coeficiente de elevação) e C D (coeficiente de arrasto). Nos dois casos, ρ é a densidade do ar (1,2 kg / m 3 ) e v é a velocidade.O que é um? Esta é a área transversal de uma pessoa (emergência no nosso caso). Em teoria, A para resistência e força de elevação deve diferir, dependendo do ângulo de ataque. Mas nem sempre sei exatamente o que estou fazendo - é por isso que verifiquei com fontes diferentes e o artigo de 2011 “ A trajetória de um Batman em queda"da revista física Journal of Physics Special Topics. Nela, os autores usaram a mesma área para resistência e sustentação, então farei o mesmo.Modelagem de trajetória
Se uma emergência pular de um prédio, até onde ele pode se mover em uma queda? Que diferença as asas de aranha lhe dão? Modelar o estado de emergência não é tão simples, pois a resistência e a elevação dependem da velocidade. Essa trajetória só pode ser calculada usando um modelo numérico no qual o movimento é dividido em pequenos passos.Vamos fazer a aproximação. Primeiro, calculamos a área de superfície da emergência. Aproximadamente, obtive: O que nos dá uma área de cerca de 0,651 m 2 com asas e 0,513 m 2 sem elas. Outros valores:• Coeficiente de elevação = 1,45 (valor retirado do trabalho de Batman)• Coeficiente de resistência = 0,4 (do mesmo local)• Peso = 64 kg• Velocidade inicial = 8 m / s (horizontal)• E mais uma suposição: um ângulo de ataque constante, em relação ao qual os coeficientes de arrasto e elevação não mudam.Sem hesitar, entrei no mundo dos modelos numéricos. Deixei comentários no código para que você possa refazê-lo para uso como lição de casa.
O que nos dá uma área de cerca de 0,651 m 2 com asas e 0,513 m 2 sem elas. Outros valores:• Coeficiente de elevação = 1,45 (valor retirado do trabalho de Batman)• Coeficiente de resistência = 0,4 (do mesmo local)• Peso = 64 kg• Velocidade inicial = 8 m / s (horizontal)• E mais uma suposição: um ângulo de ataque constante, em relação ao qual os coeficientes de arrasto e elevação não mudam.Sem hesitar, entrei no mundo dos modelos numéricos. Deixei comentários no código para que você possa refazê-lo para uso como lição de casa.GlowScript 2.1 VPython
A1=0.651
A2=0.513
g=vector(0,-9.8,0)
m=64
CL=1.45
CD=0.4
rho=1.2
v0=8
p=vector(v0,0,0)*m
p2=p
t=0
dt=0.01
h=40
r=vector(0,h,0)
r2=r
f1=series(color=color.red)
f2=series(color=color.blue)
while r.y>0:
v=p/m
v2=p2/m
Fd=-.5*rho*A1*CD*(mag(v)**2)*norm(v)
Fd2=-.5*rho*A2*CD*(mag(v2)**2)*norm(v2)
FL=-.5*rho*A1*CL*(mag(v)**2)*cross(norm(v),vector(0,0,1))
FL2=-.5*rho*A2*CL*(mag(v2)**2)*cross(norm(v2),vector(0,0,1))
F=m*g+Fd+FL
F2=m*g+Fd2+FL2
p=p+F*dt
p2=p2+F2*dt
r=r+p*dt/m
r2=r2+p2*dt/m
t=t+dt
f1.plot(r.x,r.y)
f2.plot(r2.x,r2.y)
print("Glide Ratio 1 = ",-p.x/p.y)
print("Glide Ratio 2 = ", -p2.x/p2.y)
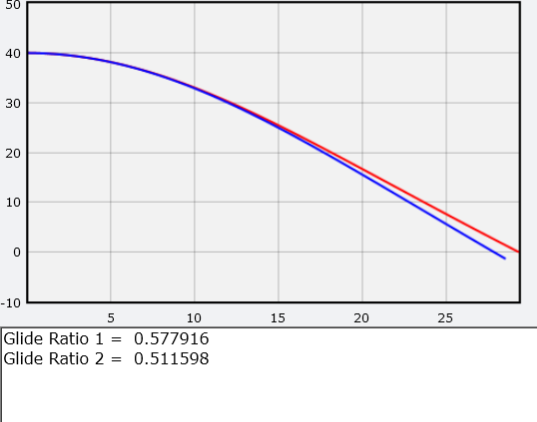 No meu modelo, a linha vermelha representa a trajetória da emergência com asas e a linha azul sem asas. Também deduzo o valor da qualidade aerodinâmica. Como no final ele se move a uma velocidade constante, essa proporção será simplesmente igual à proporção do componente x do momento dividido pelo componente y.Trabalho de casaUse este modelo numérico para responder às seguintes perguntas . Não se preocupe, você não vai quebrar nada. Se você fizer algo com o código, basta reiniciar e começar de novo.• De acordo com a Wikipedia, para um pára-quedista pulando em um traje alado, a qualidade aerodinâmica (a razão entre elevação e arrasto) tem um valor da ordem de 2,5: 1 (ou seja, nosso programa deduziria o número 2,5). Você pode corrigir o código para que o programa produz esse valor? Dica: altere a área da superfície e a velocidade inicial.• E se uma emergência cair verticalmente? Qual será a velocidade máxima com asas e sem elas?• Com que rapidez a emergência precisa se mover horizontalmente para que voe para cima e não para baixo no início do voo?• Um salto de emergência, apontando para baixo, para ganhar mais velocidade e por algum tempo entrar em vôo horizontal?• Você pode construir um modelo aprimorado que leve em consideração o ângulo de ataque? Talvez você possa, mas me parece que voar em baixa velocidade é um tópico bastante complicado.
No meu modelo, a linha vermelha representa a trajetória da emergência com asas e a linha azul sem asas. Também deduzo o valor da qualidade aerodinâmica. Como no final ele se move a uma velocidade constante, essa proporção será simplesmente igual à proporção do componente x do momento dividido pelo componente y.Trabalho de casaUse este modelo numérico para responder às seguintes perguntas . Não se preocupe, você não vai quebrar nada. Se você fizer algo com o código, basta reiniciar e começar de novo.• De acordo com a Wikipedia, para um pára-quedista pulando em um traje alado, a qualidade aerodinâmica (a razão entre elevação e arrasto) tem um valor da ordem de 2,5: 1 (ou seja, nosso programa deduziria o número 2,5). Você pode corrigir o código para que o programa produz esse valor? Dica: altere a área da superfície e a velocidade inicial.• E se uma emergência cair verticalmente? Qual será a velocidade máxima com asas e sem elas?• Com que rapidez a emergência precisa se mover horizontalmente para que voe para cima e não para baixo no início do voo?• Um salto de emergência, apontando para baixo, para ganhar mais velocidade e por algum tempo entrar em vôo horizontal?• Você pode construir um modelo aprimorado que leve em consideração o ângulo de ataque? Talvez você possa, mas me parece que voar em baixa velocidade é um tópico bastante complicado.