Em novembro, a revista Quanta intrigou seus leitores com perguntas sobre como desenhar formas a partir de objetos planos idênticos (como moedas ou dominó). Este artigo fornece perguntas e respostas detalhadas para eles.Pergunta 1
, , . . . , , ? n ?
Fisicamente, a tarefa exige equilibrar o torque da figura nos dois lados da borda da mesa. O torque de cada lado é o produto da massa desse lado e a distância do centro de massa à borda. Quando o centro de massa de toda a figura está acima da borda, o mesmo momento atua nos dois lados e o torque total do sistema é zero. Para um objeto composto, o torque total para qualquer face pode ser encontrado adicionando o torque de todos os componentes. Portanto, podemos dividir e dominar a tarefa original, considerando apenas as alterações que ocorrem quando um novo bloco é adicionado a uma pilha existente, algo como indução matemática (vamos chamá-la de indução física).Considere uma pilha de n-1 blocos, cada um dos quais pesa uma unidade de peso e tem um comprimento de uma unidade de comprimento. A pilha está equilibrada na borda da mesa. Imagine que a linha de visão é direcionada ao longo da borda da mesa, e a mesa está à esquerda - ou seja, as extremidades suspensas dos blocos se projetam para a direita. Como a pilha está equilibrada na borda, o centro de massa está logo acima da borda e seu torque é zero. Agora imagine que levantamos a pilha inteira verticalmente e colocamos outro bloco embaixo dela para que sua borda direita estivesse alinhada com a borda da mesa. Na prática, isso pode ser difícil, mas em um experimento mental é simples.Adicionamos alguma estabilidade à pilha adicionando o enésimo bloco a partir da parte inferior, pois o centro de massa de toda a pilha mudou ligeiramente para a esquerda. Indique esse deslocamento x. Os blocos n pesam n unidades e possuem um torque comum x * n ao redor da borda da tabela, direcionado para a esquerda. Lembre-se de que uma pilha de n-1 blocos tem um momento zero total. Adicionamos apenas o momento do novo bloco - com uma massa de uma unidade de massa e com uma distância do centro de massa da borda da mesa em meia unidade de comprimento.Acontece que x * n = 1/2, o que significa x = 1 / 2n, em que x é a distância do novo centro de massa a partir da borda da tabela.Isso significa que, se você mover a pilha inteira de n blocos para a direita em 1/2 de comprimento, ela estará perfeitamente equilibrada na borda - e esse é o deslocamento máximo possível. Para concluir a construção da indução, observamos que a saliência máxima do primeiro bloco a partir da borda da tabela é de 1/2 unidade de comprimento.Portanto, para cinco blocos, substituímos na fórmula n para cada nível de 1 a cinco para obter o balanço máximo:x=1/2+1/4+1/6+1/8+1/10=137/120=1,141(6)
Pode-se observar que, se você começar de cima e adicionar blocos abaixo, cada turno será metade do inverso do número de blocos disponíveis. Tais seqüências de números inversos são conhecidas como séries harmônicas. Essa série diverge lentamente e, como n tende ao infinito, também tende ao infinito.A fórmula geral da soma para n blocos é obtida somando todos os membros da série. Acontece metade do enésimo termo harmônico, que pode ser escrito como:Questão 2
Imagine que você tem os mesmos cinco blocos e deseja colocar um pouco de decoração no topo deles, a um ponto de um quarto do comprimento do bloco da extremidade pendurada. Todos os blocos pesam uma unidade de peso e as jóias pesam um quinto do bloco. Qual é o comprimento máximo do balanço agora? Como isso muda a fórmula básica?
Primeiro, considere o primeiro bloco com a decoração em pé e apoie-a de forma que a borda direita fique nivelada com a borda da mesa. O centro de massa do bloco sem decoração fica a meia unidade de comprimento da borda da mesa. A decoração irá movê-lo para a direita, digamos, por x. A massa da decoração é 1/5 e a distância do novo centro de massa será 1/4. Equacionamos os momentos e obtemos x = 1/5 * (1/4 x), portanto, x = 1/24. Devido à decoração, é necessário mover o primeiro bloco para a esquerda em 1/24 do comprimento, para que a saliência máxima seja agora 11/24 em vez de 1/2.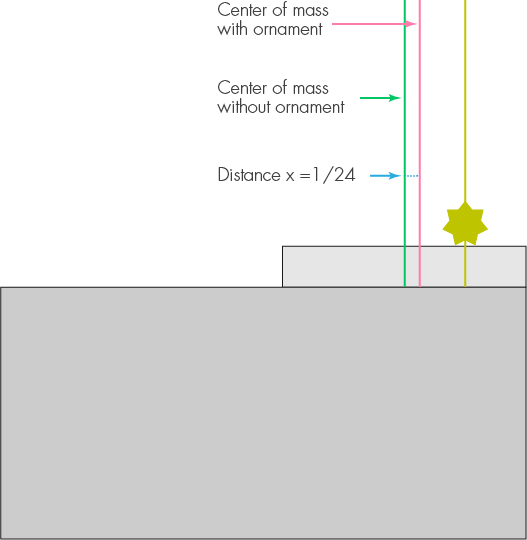
Pergunta 3
, , . . . , . , , . , ?
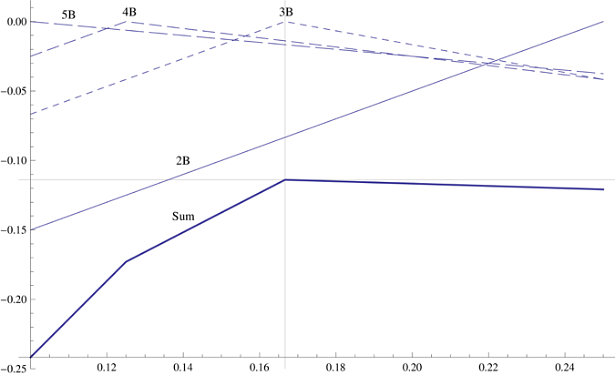
Como a probabilidade de ter de dois a cinco blocos é a mesma, você precisa maximizar a quantidade que indica a saliência máxima para esses quatro casos. Para uma pilha de 2 a 5 blocos, existe uma posição ideal do primeiro bloco, oferecendo o balanço máximo de toda a pilha. Se você construir a maior saliência no gráfico para cada um dos quatro tamanhos possíveis da próxima pilha, obterá dois gráficos de linha e dois na forma de um V. invertido. Seus vértices indicam a posição inicial ideal do bloco inicial para pilhas de 3-4 blocos. Resumindo os gráficos, obtemos o gráfico de balanço geral, que muda drasticamente a direção em cada uma das quatro posições ideais. Acontece que o melhor balanço geral é alcançado na posição ideal para os três blocos, após o que o gráfico diminui. Portanto, você precisa colocar o bloco original sob a suposiçãoque você receberá três blocos adicionais e a saliência terá 1/6 unidades de comprimento.