Há 70 anos, em 16 de dezembro de 1947, nos laboratórios da Bell Labs, John Bardin e Walter Brattain, sob a direção de William Shockley, criaram o primeiro transistor bipolar operacional. Em 23 de dezembro, Brattain demonstrou a seus colegas o primeiro amplificador de transistor. Portanto, esse dia costuma ser chamado de Dia do Transistor . Não há necessidade de falar sobre o significado deste evento. O transistor é considerado uma das invenções mais importantes do século XX, sem as quais os computadores ainda funcionariam com lâmpadas e relés e ocupariam edifícios inteiros. Shockley, Bardin e Brattain receberam o Prêmio Nobel de Física por seu trabalho em 1956. Ao longo dos anos, o transistor miniaturizou para apenas alguns átomos. Cada processador possui bilhões de transistores, de modo que o transistor pode ser chamado de dispositivo mais massivo criado pela humanidade.Mas que tipo de trabalho o transistor faz por nós? Vamos fazer uma jornada mental: traçaremos o caminho desde as pontas dos dedos de alto nível até o nosso aniversário - transistor.O que levar como ponto de partida? Bem, pelo menos desenhe um botão habrakat.
Não há necessidade de falar sobre o significado deste evento. O transistor é considerado uma das invenções mais importantes do século XX, sem as quais os computadores ainda funcionariam com lâmpadas e relés e ocupariam edifícios inteiros. Shockley, Bardin e Brattain receberam o Prêmio Nobel de Física por seu trabalho em 1956. Ao longo dos anos, o transistor miniaturizou para apenas alguns átomos. Cada processador possui bilhões de transistores, de modo que o transistor pode ser chamado de dispositivo mais massivo criado pela humanidade.Mas que tipo de trabalho o transistor faz por nós? Vamos fazer uma jornada mental: traçaremos o caminho desde as pontas dos dedos de alto nível até o nosso aniversário - transistor.O que levar como ponto de partida? Bem, pelo menos desenhe um botão habrakat.HTML e CSS
Um botão consiste em pixels de fundo, texto e borda. No código, definido pela tag <a>, à qual as regras de layout CSS são aplicadas. Por exemplo, uma regra CSS é aplicada a uma borda nos cantos arredondados:border-radius: 3px;
 Assim, o limite consiste em quatro segmentos e quatro arcos ("quartos" de um círculo).
Assim, o limite consiste em quatro segmentos e quatro arcos ("quartos" de um círculo).Navegador
Para pesquisa, peguei meu Firefox favorito. Antes de o FF começar a desenhar o nosso botão, ele precisa trabalhar muito na análise e no cálculo da posição dos elementos:- Baixe HTML em uma rede, analise, componha uma árvore DOM
- Faça o download pela rede CSS, realize análise lexical, analise
- Vincular regras com base na prioridade e herança aos elementos da página
- Para todos os nós DOM visíveis, componha uma árvore de suas áreas retangulares - quadros.
- Para quadros, calcule as dimensões e a localização (consulte o vídeo )
- Componha camadas de quadros, levando em consideração o índice z e o tipo de conteúdo (<canvas>, SVG, <video>).
- Crie uma lista de desenhos em ordem: cor de fundo, imagem de fundo, borda, descendentes, estrutura de tópicos.
Adicionar. materiais de leitura: Não vamos nos aprofundar nessas etapas em detalhes. Depois deles, vem o desenho real dos elementos necessários.Faça o download da fonte para descobrir o que está acontecendo lá,Mozilla Firefox.
Firefox Mercurial Visual Studio C++. VS
symbols.mozilla.org. - /layout/.
, , , Firefox. c , , — FF.
O arquivo nsCSSRenderingBorders.cpp é responsável pelo desenho das bordas . E a função geral de desenhar bordas é chamada (quem teria pensado): DrawBorders () . A função seleciona o método de renderização ideal para várias situações. Temos um caso relativamente simples: existe um raio de borda, mas as bordas de todos os lados são sólidas e da mesma cor.Nosso seif (allBordersSame &&
mCompositeColors[0] == nullptr &&
mBorderStyles[0] == NS_STYLE_BORDER_STYLE_SOLID &&
!mAvoidStroke &&
!mNoBorderRadius)
{
gfxRect outerRect = ThebesRect(mOuterRect);
RoundedRect borderInnerRect(outerRect, mBorderRadii);
borderInnerRect.Deflate(mBorderWidths[eSideTop],
mBorderWidths[eSideBottom],
mBorderWidths[eSideLeft],
mBorderWidths[eSideRight]);
RefPtr<PathBuilder> builder = mDrawTarget->CreatePathBuilder();
AppendRoundedRectToPath(builder, mOuterRect, mBorderRadii, true);
AppendRoundedRectToPath(builder, ToRect(borderInnerRect.rect), borderInnerRect.corners, false);
RefPtr<Path> path = builder->Finish();
mDrawTarget->Fill(path, color);
return;
}
Existem opções muito mais complexas, como ancorar em cantos com raio de borda de diferentes tipos de bordas pontilhadas e tracejadas, consulte DrawDashedOrDottedCorner () . Existe no código completamenteMas voltando ao nosso se. Com o comentário, aprendemos que, nesse caso, a borda é desenhada usando dois retângulos - interno e externo, e o caminho (caminho) criado é preenchido com a cor desejada.AppendRoundedRectToPath(builder, mOuterRect, mBorderRadii, true);
AppendRoundedRectToPath(builder, ToRect(borderInnerRect.rect), borderInnerRect.corners, false);
RefPtr<Path> path = builder->Finish();
mDrawTarget->Fill(path, color);
Vá para AppendRoundedRectToPath () em gfx / 2d / PathHelpers.cpp.Mais uma vez, estabelecemos pontos de interrupção Aprendemos com o comentário sobre a função de que os cantos são desenhados em quatro pontos de controle pelas curvas de Bezier . As curvas de Bezier são frequentemente usadas em computação gráfica, inclusive para desenhar arcos de círculos e elipses. Conforme aprendemos mais com o comentário, há muitas opções para escolher pontos de controle para construir uma curva. Nesse caso, precisamos que os pontos 0 e 3 pertençam aos lados do retângulo, os pontos 0, 1 e C estejam em uma linha reta, os pontos 3, 2 e C na outra. Veja a figura: Resta calcular a relação dos comprimentos dos segmentos 01 / 0C e 32 / 3C. Aqui, os autores usam cálculos aproximados e obtêm a constante mágica alfa:
Resta calcular a relação dos comprimentos dos segmentos 01 / 0C e 32 / 3C. Aqui, os autores usam cálculos aproximados e obtêm a constante mágica alfa:const Float alpha = Float(0.55191497064665766025);
Infelizmente, artigos com o algoritmo de seleção de ponto de verificação referenciado pelo comentário não são de domínio público. Mas, em geral, deve-se notar que, em computação gráfica, os algoritmos costumam usar aproximação para melhorar o desempenho. Por exemplo, o algoritmo de Brezenham permite desenhar segmentos e círculos não "na testa" - resolvendo as equações y = f (x), mas com operações inteiras mais astutas. A mesma coisa com preenchimento, etc.Além disso, no ciclo, vamos de canto a canto, use alfa para calcular as coordenadas dos pontos de controle e, finalmente, chame as funções de desenhar a linha de borda e o arco do canto:aPathBuilder->LineTo(p0);
aPathBuilder->BezierTo(p1, p2, p3);
Adicionar. material de leitura Código AppendRoundedRectToPath () completovoid
AppendRoundedRectToPath(PathBuilder* aPathBuilder,
const Rect& aRect,
const RectCornerRadii& aRadii,
bool aDrawClockwise)
{
const Float alpha = Float(0.55191497064665766025);
typedef struct { Float a, b; } twoFloats;
twoFloats cwCornerMults[4] = { { -1, 0 },
{ 0, -1 },
{ +1, 0 },
{ 0, +1 } };
twoFloats ccwCornerMults[4] = { { +1, 0 },
{ 0, -1 },
{ -1, 0 },
{ 0, +1 } };
twoFloats *cornerMults = aDrawClockwise ? cwCornerMults : ccwCornerMults;
Point cornerCoords[] = { aRect.TopLeft(), aRect.TopRight(),
aRect.BottomRight(), aRect.BottomLeft() };
Point pc, p0, p1, p2, p3;
if (aDrawClockwise) {
aPathBuilder->MoveTo(Point(aRect.X() + aRadii[RectCorner::TopLeft].width,
aRect.Y()));
} else {
aPathBuilder->MoveTo(Point(aRect.X() + aRect.Width() - aRadii[RectCorner::TopRight].width,
aRect.Y()));
}
for (int i = 0; i < 4; ++i) {
int c = aDrawClockwise ? ((i+1) % 4) : ((4-i) % 4);
int i2 = (i+2) % 4;
int i3 = (i+3) % 4;
pc = cornerCoords[c];
if (aRadii[c].width > 0.0 && aRadii[c].height > 0.0) {
p0.x = pc.x + cornerMults[i].a * aRadii[c].width;
p0.y = pc.y + cornerMults[i].b * aRadii[c].height;
p3.x = pc.x + cornerMults[i3].a * aRadii[c].width;
p3.y = pc.y + cornerMults[i3].b * aRadii[c].height;
p1.x = p0.x + alpha * cornerMults[i2].a * aRadii[c].width;
p1.y = p0.y + alpha * cornerMults[i2].b * aRadii[c].height;
p2.x = p3.x - alpha * cornerMults[i3].a * aRadii[c].width;
p2.y = p3.y - alpha * cornerMults[i3].b * aRadii[c].height;
aPathBuilder->LineTo(p0);
aPathBuilder->BezierTo(p1, p2, p3);
} else {
aPathBuilder->LineTo(pc);
}
}
aPathBuilder->Close();
}
Mas tudo depende do back-end dos gráficos 2D que a Mozilla usa.Mecanismo de gráficos
O Gecko usa a biblioteca Moz2D independente da plataforma, que por sua vez pode usar um dos back-ends: Cairo, Skia, Direct2D, Quartz e NV Path. Por exemplo, Direct2D, Cairo, Skia estão disponíveis para Windows. O Skia também é o back-end do Chromium. Você pode alterar o back-end em about: config. Os back-ends, por sua vez, podem ler tudo na CPU, ou podem usar a aceleração de hardware da GPU até certo ponto. Por exemplo, a Skia possui seu próprio back-end OpenGL - Ganesh.O código do Direct2D está fechado, por isso, é melhor ativar o Skia e ver o que ele faz. A função para desenhar uma curva cúbica SkPath :: cubicTo é chamada. Para construir uma curva, ela é dividida pelo algoritmo de Castelljo em vários segmentos retos, que são realmente desenhados (consulte core / SkGeometry.cpp).Adicionar. materiais de leitura Código da máquina
Para ser sincero, não consegui entender completamente os componentes internos do Skia, então dei um passo atrás - para AppendRoundedRectToPath (), onde todas as operações são executadas em números inteiros - o que poderia ser mais fácil?Após abrir o código desmontado, precisamos encontrar a operação de adição nele....
142B1863 00 00 add byte ptr [eax],al
142B1865 00 8D 43 FF 0F 84 add byte ptr [ebp-7BF000BDh],cl
142B186B 67 01 00 add dword ptr [bx+si],eax
142B186E 00 99 0F 57 C9 F7 add byte ptr [ecx-836A8F1h],bl
142B1874 F9 stc
142B1875 8B C3 mov eax,ebx
142B1877 8B CA mov ecx,edx
142B1879 99 cdq
142B187A F7 7C 24 28 idiv eax,dword ptr [esp+28h]
...
Sim! Mesmo uma pessoa tão distante do ASM quanto eu posso imaginar facilmente que a operação ADD é responsável pela adição. Faça a primeira operação:142B1863 00 00 add byte ptr [eax],al0x142B1863 - endereço na RAM0x00 - opcode - código de instrução do processador. Este Mozilla compilado sob x86 e abrindo a tabela de instruções x86 , veremos que o código 00 significa uma operação de adição de 8 bits com mnemônicos ADD. O primeiro operando pode ser um registro ou uma célula de memória de acesso aleatório, o segundo pode ser um registro. O primeiro operando é adicionado ao segundo, o resultado é gravado no primeiro. Explicarei, por precaução, que o registro é uma memória RAM ultra-rápida dentro do processador, por exemplo, para armazenar resultados de cálculos intermediários.O segundo byte também é 0x00 e é chamado MOD-REG-R / M. Seus bits especificam os operandos e o método de endereçamento. MOD = 00b em combinação com R / M = 000b significa que o endereçamento indireto é usadoREG = 000b significa que o registro AL é usado (os 8 bits mais baixos do registro EAX)[eax] - indica que a adição é feita com a célula RAM, cujo endereço está no registro EAX.Comoo processador processa o comando ADD?
MOD = 00b em combinação com R / M = 000b significa que o endereçamento indireto é usadoREG = 000b significa que o registro AL é usado (os 8 bits mais baixos do registro EAX)[eax] - indica que a adição é feita com a célula RAM, cujo endereço está no registro EAX.Comoo processador processa o comando ADD?CPU
Com base na descrição da microarquitetura Skylake , compilei uma lista (extremamente simplificada) de etapas:- As instruções X86 são buscadas de um cache de instruções L1 de 32 KB em um buffer de pré-codificação de 16 bytes
- Os comandos pré-codificados são organizados na Fila de instruções (tamanho 2 x 25) e entram nos decodificadores
- x86 1-4 (µOPs). ADD 1 µOP ALU (- ) 2 µOP AGU ( ) (., ). 86 .
- Allocation Queue (IDQ). , Loop Stream Detector — .
- : , . . .
- A microoperação vai para o gerente do Unified Scheduler, que decide em que ponto e em qual porta enviar operações para execução fora de ordem de recebimento. Atrás de cada porta está um atuador. Nossas micro operações irão para ALU e AGU.
 O núcleo do SkyLake. Imagem de en.wikichip.org .Repito, esta é minha descrição muito simplificada e não pretende ser precisa e completa. Para referência adicional, recomendo a leitura do post Journey através do pipeline de computação do processador e do artigo Processadores da família Intel Core i7
O núcleo do SkyLake. Imagem de en.wikichip.org .Repito, esta é minha descrição muito simplificada e não pretende ser precisa e completa. Para referência adicional, recomendo a leitura do post Journey através do pipeline de computação do processador e do artigo Processadores da família Intel Core i7ALU
Agora, seria interessante saber o que está acontecendo na ALU: como os números são somados? Infelizmente, as informações sobre a implementação específica da microarquitetura e da ALU são o segredo comercial da Intel, por isso voltamos à teoria posteriormente.Um dispositivo para adicionar dois bits binários (isto é, um bit) é chamado somador . A saída é a soma e o bit de transporte. Fonte: WikipediaDesde na vida real, precisamos adicionar números que consistem em vários dígitos, o somador também deve aceitar o bit de transporte do dígito anterior como entrada. Esse somador é chamado de cheio .
Fonte: WikipediaDesde na vida real, precisamos adicionar números que consistem em vários dígitos, o somador também deve aceitar o bit de transporte do dígito anterior como entrada. Esse somador é chamado de cheio .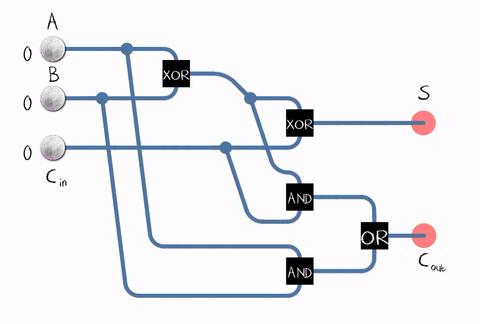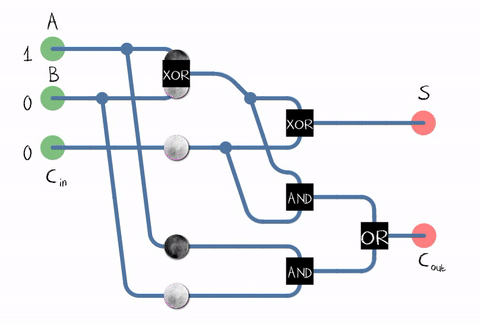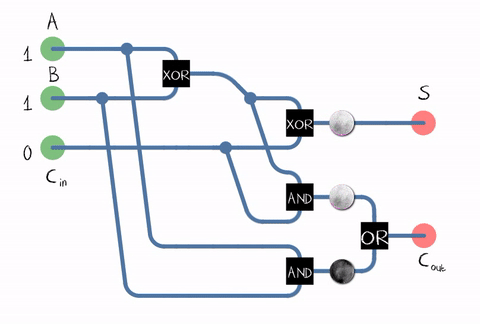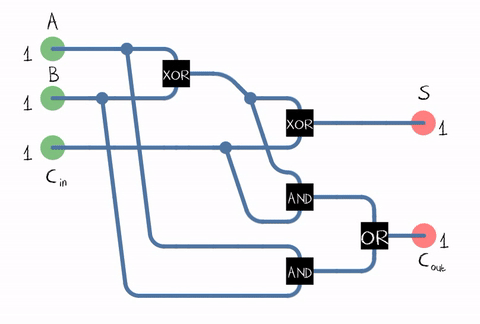 Fonte: WikipediaComo pode ser visto na figura, o somador é composto por elementos lógicos: XOR, AND, OR. E todo elemento lógicopode ser implementado usando vários transistores. Ou mesmo um revezamento .
Fonte: WikipediaComo pode ser visto na figura, o somador é composto por elementos lógicos: XOR, AND, OR. E todo elemento lógicopode ser implementado usando vários transistores. Ou mesmo um revezamento . Um exemplo de implementação de um somador completo em transistores CMOS . FonteEntão chegamos ao transistor! Embora, é claro, não apenas as ALUs funcionem em transistores, mas também em outras unidades processadoras, mas a maioria dos transistores é usada no cache como suas células.Na realidade, o circuito somador em nosso processador pode ser construído de maneira diferente e muito mais complicado. Por exemplo, a Intel 8008, há 45 anos, já era capaz de calcular todos os bits de transporte com antecedência para realizar a adição em paralelo (o chamado somador com transporte paralelo). Quem se importa, leia a interessante postagem no blog sobre engenharia reversa ALU Intel 8008 no blogKen Shirriff. I.e. várias otimizações são usadas: por exemplo, a multiplicação também é benéfica para não ser feita "de frente".
Um exemplo de implementação de um somador completo em transistores CMOS . FonteEntão chegamos ao transistor! Embora, é claro, não apenas as ALUs funcionem em transistores, mas também em outras unidades processadoras, mas a maioria dos transistores é usada no cache como suas células.Na realidade, o circuito somador em nosso processador pode ser construído de maneira diferente e muito mais complicado. Por exemplo, a Intel 8008, há 45 anos, já era capaz de calcular todos os bits de transporte com antecedência para realizar a adição em paralelo (o chamado somador com transporte paralelo). Quem se importa, leia a interessante postagem no blog sobre engenharia reversa ALU Intel 8008 no blogKen Shirriff. I.e. várias otimizações são usadas: por exemplo, a multiplicação também é benéfica para não ser feita "de frente".Conclusões: o que aprendemos?
- É complicado
- É claramente mostrado: para resolver o problema da complexidade excessiva, os engenheiros usam a divisão de sistemas complexos em níveis (camadas).
- Arquiteturas multinível fornecem portabilidade: por exemplo, o Firefox pode ser executado em vários sistemas operacionais e em diferentes hardwares.
- A interação entre os níveis se deve à abertura de especificações para interfaces, serviços e formatos de dados, por exemplo, HTML e CSS, C ++, um conjunto de comandos x86, etc.
- Nosso herói do dia está trabalhando bem no fundo - um transistor .
PS Sou amador (desenvolvedor web) e conheço bastante a arquitetura C ++, ASM, BT - pelo curso do instituto, eu poderia estragar alguma coisa. Por favor, sinta-se livre para enviar comentários.