Como criar papéis de parede impossíveis: uma história de simetrias proibidas

À esquerda, há um padrão de papel de parede com simetria de rotação de sexta ordem em torno de cada uma das rosetas verde-marrom. À direita, há um padrão de papel de parede com simetria de espelho em relação às linhas horizontais que passam por cada elemento elíptico de um ornamento de vitral.

À primeira vista, inventar um papel de parede não é mais difícil do que concluir tarefas de um jardim de infância. Os designers podem escolher qualquer combinação de cores e formas para a peça original e simplesmente multiplicá-la em duas direções. Dependendo do padrão da peça inicial e da escolha das direções, simetrias adicionais podem aparecer - por exemplo, simetria de sexta ordem na primeira foto ou simetria de espelho na segunda. Ambos os padrões foram criados pelo matemático Frank Farris, da Universidade da Califórnia, Santa Clara.


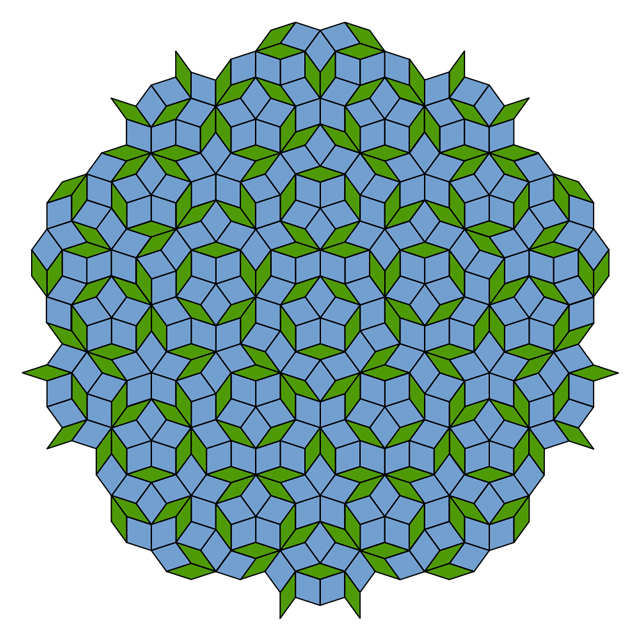Os mosaicos de Penrose mostram muitos exemplos de simetria local de quinta ordem, mas eles não têm repetições do padrão. Ao preencher grandes áreas no plano, a proporção entre o número de ladrilhos largos e o número de estreitos se aproxima da proporção áurea.

Porém, embora seja possível criar papéis de parede com simetrias rotacionais de segunda, terceira, quarta ou sexta ordens, é impossível criar papéis de parede com simetria de quinta ordem [a ordem mostra quantas vezes o padrão se alinhará automaticamente durante a rotação de 360 ​​° - aprox. transl.]. Essa restrição é conhecida pelos matemáticos há quase 200 anos como uma "restrição cristalográfica". A geometria do pentágono proíbe padrões com simetria de quinta ordem. O mesmo vale para pedidos de sete ou mais.

No entanto, os padrões mais interessantes, como os ladrilhos de Penrose, mostram simetria local de quinta ordem em muitos lugares e em escalas diferentes, apenas sem repetir os padrões. Usando um método diferente da abordagem de Penrose, Farris restringiu a incomum geometria de simetria de quinta ordem e criou um novo conjunto de imagens interessantes - pseudo-papéis de parede que parecem não obedecer, à primeira vista, a restrição cristalográfica.


Fig. 4 A

quarta figura parece um contra-exemplo de restrição cristalográfica, possuindo simetria rotacional de quinta ordem em torno do ponto A, enquanto o padrão pode ser deslocado em um plano nas direções AB ou AC. De fato, Faris escreve em seu artigo para a revista Notices of the American Mathematics Society que essa imagem é apenas uma farsa inteligente.

"Você sabe que a simetria que observa é impossível", diz Stephen Kennedy, do Carleton College, em Minnesota.

A simetria rotacional de quinta ordem em torno do ponto A parece ter sido cumprida. Mas se você observar atentamente, notará que as rodas ao redor dos pontos B e C são ligeiramente diferentes de A. Se pudéssemos nos afastar do padrão para ver mais repetições, as repetições visíveis do padrão seriam cada vez menos como um padrão na região do ponto E, mesmo que cópias cada vez mais convincentes de A apareçam em outros lugares, como na Fig. 5. Faris mostrou que essas ilusões também podem ser criadas em uma escala maior, afastando-se do padrão e repetindo-o um certo número de vezes - especificamente, o número de vezes correspondente aos números da série Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, ... onde cada número a seguir é a soma dos dois anteriores), que também desempenha um papel na geometria dos ladrilhos Penrose.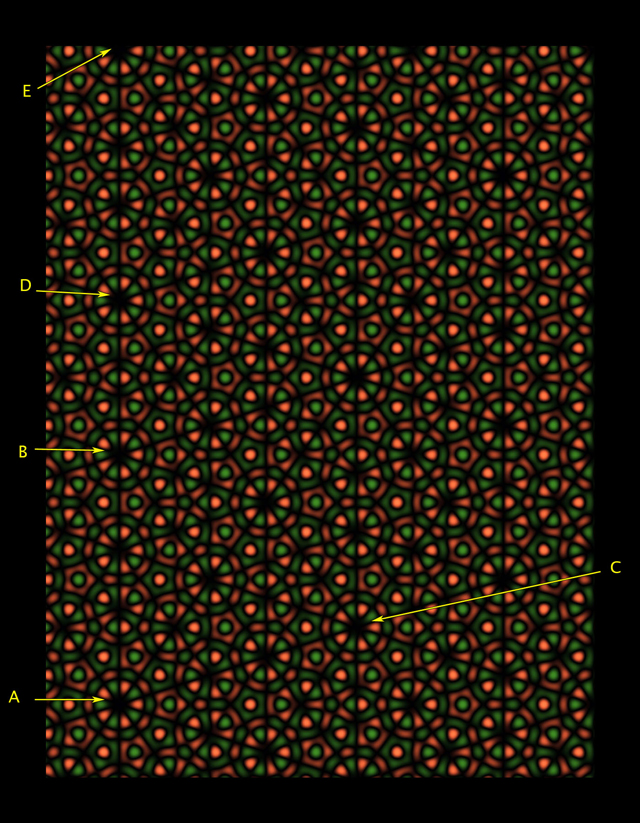


Fig. 5

"Por razão, entendemos que isso é algum tipo de engano", diz Faris. No entanto, como ele escreve no artigo, essas imagens "convidam nossos olhos a estudá-las e desfrutar de repetições quase perfeitas".

Faris pensou nessas falsificações, mudando a tecnologia com a qual ele criou papéis de parede reais com simetria rotacional de 3ª ordem, como na Fig. 6

Para criar simetria de terceira ordem, Faris começou a trabalhar no espaço tridimensional, que possui uma rotação especialmente natural, classificando através de três coordenadas espaciais e pontos de rotação no espaço 120 graus em torno da diagonal. Então Faris criou padrões tridimensionais de papel de parede, sobrepondo sinusóides especialmente selecionados e combinando-os com uma paleta de cores pré-selecionada. Os pontos foram corados dependendo da posição dos sinusóides sobrepostos. Então Faris apresentou um papel de parede plano, limitando essa cor a um plano bidimensional perpendicular ao eixo de rotação do espaço original.

Essa abordagem sinusoidal suave para criar padrões de papel de parede é diferente do método tradicional de copiar e colar, diz Kennedy. "Esta é uma maneira muito nova de criar padrões simétricos."


Fig. 6

O mesmo procedimento realizado no espaço tridimensional, ao que parece, deveria ter levado à criação de um padrão com simetria de quinta ordem - se não soubéssemos que isso é impossível. Curiosamente, pensou Faris, em que ponto esse sistema falha?

Teoricamente, o espaço tridimensional é possível, embora seja difícil de imaginar. Ele tem um análogo natural da simetria de rotação de quinta ordem, como no espaço tridimensional - a simetria da terceira. No espaço tridimensional, um dos dois planos pode ser selecionado, cada um dos quais é perpendicular ao eixo de rotação e o outro plano. Cada um deles pode ser girado em torno de um ponto em 72 ou 144 graus. Pode parecer difícil imaginar dois planos e uma linha reta perpendicular um ao outro, mas em cinco dimensões todos eles têm espaço suficiente.

Faris entendeu o problema - se um plano perpendicular corta com precisão o espaço tridimensional e contém papéis de parede infinitos com um número infinito de pontos com coordenadas inteiras, então dois planos perpendiculares no espaço cinco-dimensional são irracionais e não contêm pontos com coordenadas inteiras (exceto o ponto de referência) . Como o padrão de papel de parede criado a partir de sinusóides é repetido através de turnos por números inteiros, esses planos não herdam padrões de espaços de ordem superior.

"É assim que a mosca aparece na sopa", escreve Faris no artigo.

No entanto, a ilusão da estrutura do papel de parede aparece nesses dois planos, graças à participação dos chamados a proporção áurea, um número irracional que descreve as direções de dois planos e os números de Fibonacci.

Graças a seus relacionamentos, Faris conseguiu mostrar que, embora não haja pontos com coordenadas inteiras em dois planos, cada um deles se aproxima muito da dispersão infinita de pontos com coordenadas inteiras, cujas coordenadas são números de Fibonacci. Cada vez que o avião se aproxima de um desses pontos de Fibonacci, o padrão parece quase o mesmo do ponto de referência, o que cria a ilusão de uma cópia exata.



Faris também descobriu como combinar as cores e os padrões das fotos da natureza com as funções das ondas para incluí-las no design dos padrões, como resultado, você pode obter um grande número de papéis de parede "falsos". Na figura acima, você pode ver os galhos das árvores que migraram da fotografia.

Source: https://habr.com/ru/post/pt400591/