Tautologias importantes na ciência. Parte 1. Física

Você sabe o que é uma tautologia lógica? Você provavelmente sabe. E caso você não saiba disso, o autor tentará explicar esse conceito agora. Não começaremos a mudar para a linguagem formal e seca da matemática, não seremos pedantes sem alma como a Wikipedia e diremos figurativamente: uma tautologia é uma espécie de Ouroboros mordendo o próprio rabo. Por exemplo, "nada é quando não há nada" ou "objetos estreitos e baixos o suficiente para passar por essa porta passarão facilmente por ela" e assim por diante. Tais declarações são sempre verdadeiras e, grosso modo, não trazem nenhuma informação nova. Surpreendentemente, várias leis e princípios importantes da ciência contêm tautologias ocultas, o que, no entanto, não diminui sua importância e correção. Interessante? Então vá em frente, sob o corte!

O imperador Sarlac Grant Scenticus III estava entediado. Muito chato. Geralmente, quando se sentia entediado, jogava pedras (um jogo bastante simples, mas complicado, semelhante ao mesmo tempo que as nossas damas, reversi e Go ). No entanto, hoje nenhum dos filósofos que costumava brincar com ele veio. Ele ficou olhando e olhou para uma das posições.

O experimentador interno de Grant decidiu contar o número de posições possíveis. Vamos deixá-lo neste lugar e fazer nossa própria contagem.

De acordo com as regras, é permitido ter até 3 pedras em uma célula. Existem 6 pedras no total (3 para cada jogador). Não consideraremos o número de todas as posições possíveis. É muito mais interessante calcular quantas maneiras você pode definir uma posição. Mas primeiro, olhe o desenho.

Para simplificar, estamos considerando apenas uma célula. A posição acima pode ser obtida, por exemplo, de três maneiras que diferem em quais pedras colocamos no quadro: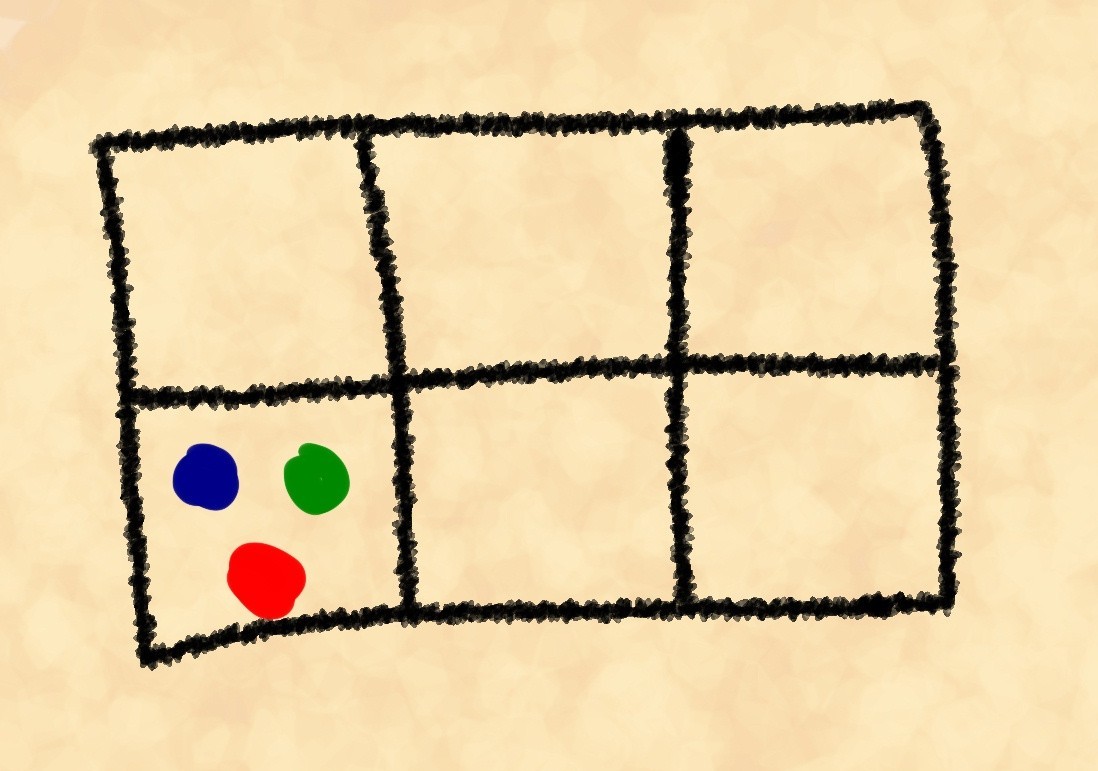

  

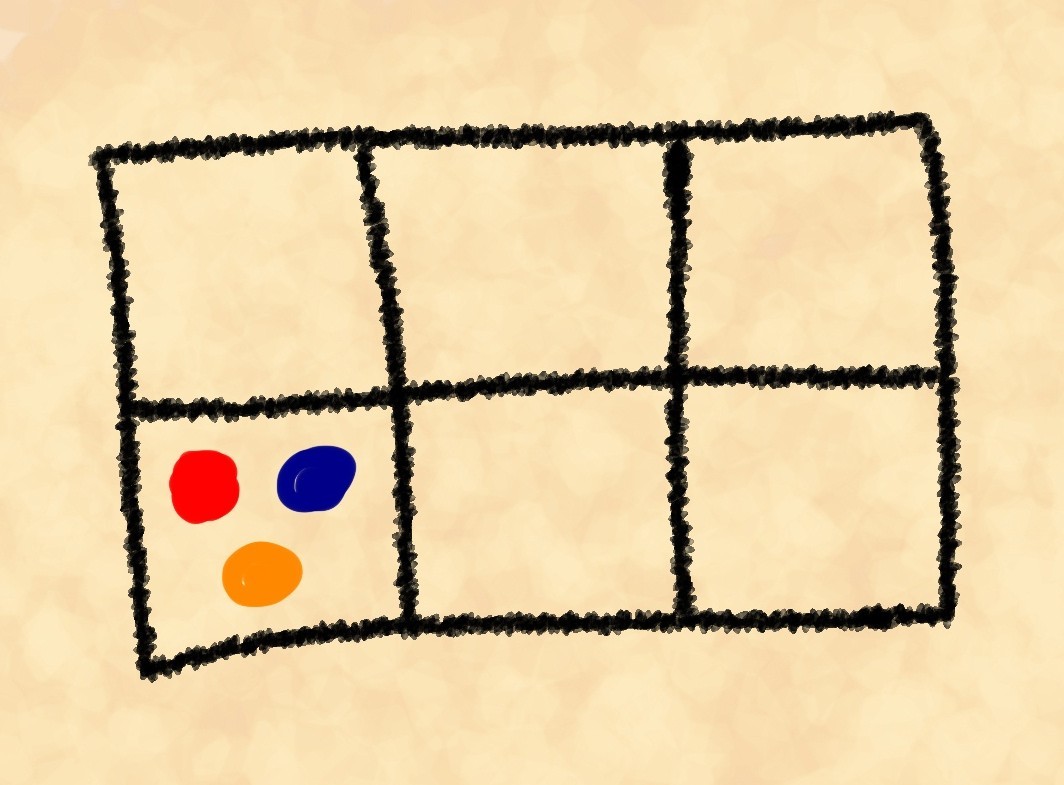pintamos condicionalmente as pedras para podermos distingui-las uma da outra. Obviamente, existem muitos mais de três métodos. Mas quanto exatamente? A primeira das três pedras que podemos escolher de seis maneiras. Cada uma dessas seis opções continua com a escolha da segunda pedra entre as cinco restantes e a última das quatro restantes. Nós temos$$ , no entanto, ao mesmo tempo, permitimos repetições, por exemplo, vermelho-azul-amarelo, amarelo-vermelho-azul e azul-vermelho-amarelo são o mesmo “cálculo”. Para encontrar o número de repetições, descobrimos de quantas maneiras podemos colocar três pedras da mesma cor no quadro. A primeira pode ser uma das três pedras necessárias, a segunda deve ser uma das duas restantes, a terceira será a última pedra que precisamos:$6\cdot5\cdot4=120$

$$. Como resultado, temos 120/6 = 20 maneiras de dispor as pedras da maneira necessária. Vamos chamar esse número do peso dessa posição. Obviamente, isso não tem nada a ver com peso físico, apenas esse nome geralmente é aceito nas estatísticas. Vamos complicar a tarefa. Vamos calcular os pesos dessas posições: Se você estiver com preguiça de entender toda essa matemática, pule o próximo parágrafo. Primeira posição:$3\cdot2\cdot1=6$




  

1. Espalhamos duas pedras em uma das duas células esquerdas: $$$2\cdot6\cdot5/2=30$
2. Na segunda célula, colocamos duas pedras das 4 restantes: $$$4\cdot3/2=6$
3. Total que temos $$$30\cdot6/2=90$.

$$$30\cdot4\cdot3/2=180$$$. A divisão em todos os casos é realizada para se livrar das repetições.$4\cdot6\cdot3\cdot5\cdot2\cdot4\cdot3/24=360$

Portanto, temos os seguintes pesos: 90 para o primeiro layout, 180 para o segundo e 360 ​​para o terceiro. Você percebeu que, quanto mais simplificada a posição, menor é o seu peso? Sua Majestade Grant notou isso. E agora ele vai calcular o peso para posições de jogo reais.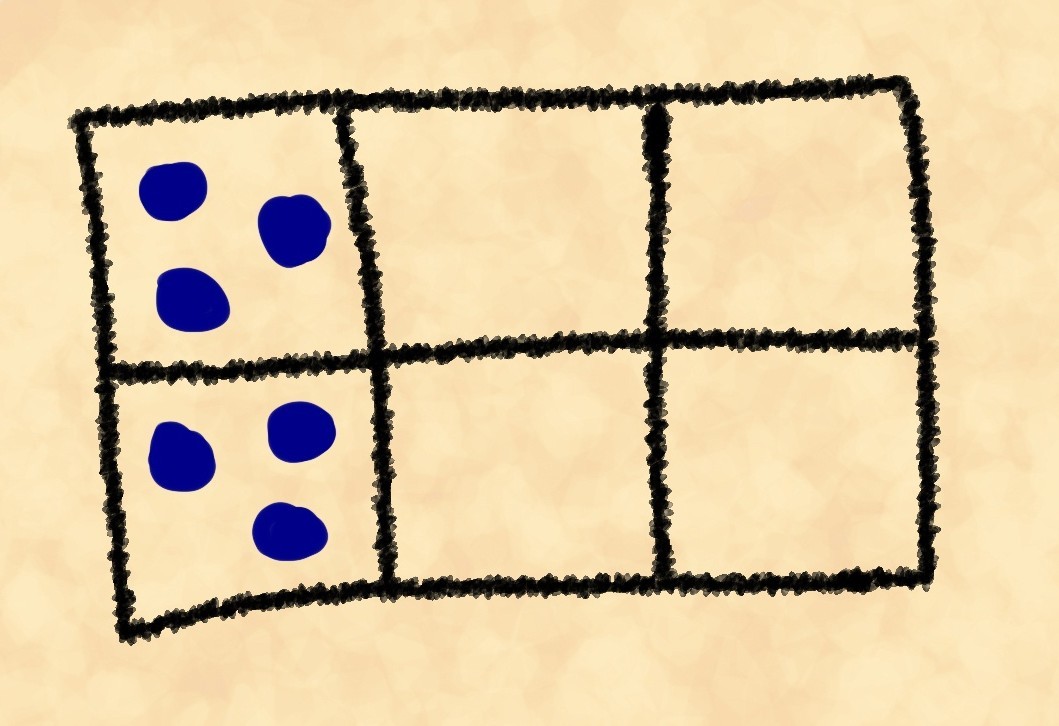

  

Ele aparece, respectivamente, 90, 360 e 720. No entanto, aqui sua paciência termina (como provavelmente a sua). Ele empurra a placa, espalhando aleatoriamente as pedras, e percebe o filósofo Klofzus parado na porta.

“Diga-me, filósofo”, ele pergunta com uma nota de descontentamento, “por que, quando eu empurro o tabuleiro, as pedras voam ao redor aleatoriamente, uniformemente, e não cabem três em uma gaiola da borda?

Klofzius, em resposta a isso, sorriu e disse:

"Eu observei seus cálculos por um tempo, senhor, e você provavelmente já poderia responder a essa pergunta." Mas eu ainda direi - pedras podem ser encomendadas da borda do tabuleiro de noventa maneiras diferentes, e setecentos e vinte podem ser espalhados por todas as células. Para pedras, há muito mais maneiras de se espalhar uniformemente pelo tabuleiro do que coletar na borda.

Talvez aqui deixemos Sarlak. Mas preste atenção à explicação de Klofzus: as pedras se espalham no tabuleiro, porque há muito mais maneiras de serem espalhadas uniformemente do que dispostas de maneira ordenada. E a diferença entre o número de métodos (os pesos dos layouts de pedras) quanto maior, maior o tabuleiro e o número de pedras. Para uma placa de 15 células (3 por 5) e 15 pedras, o peso de um layout totalmente ordenado (3 pedras por célula ao longo de uma borda) é de aproximadamente 1,4 milhão (1.401.400 se exatamente) e para um uniforme (um em cada célula) - aproximadamente 1,3 quadrilhão isto é, quase um milhão de vezes mais. Portanto, nesse caso, é muito mais fácil bagunçar do que fazer um pedido. Involuntariamente, recorda-se uma afirmação tão maravilhosa: “Os ovos quebram a cada passo, mas ninguém nunca viu,para que os fragmentos de um ovo quebrado se juntem e se tornem um ovo inteiro. E tudo porque existe apenas uma maneira de obter um ovo inteiro e infinitas maneiras de quebrar. ”

Para resumir a regularidade, notamos:

Em qualquer processo que ocorra por si só, sem influência externa adicional, é provável que o resultado que pode ser alcançado da maior quantidade possível de maneiras.

Dê uma olhada, é uma tautologia em toda a sua glória. Para simplificar as coisas, afirmo simplesmente que "o que é mais fácil acontecer acontece com mais frequência". No entanto, é também uma das leis físicas mais importantes. Muitos de vocês provavelmente já entenderam que estamos falando da segunda lei da termodinâmica. Vejamos uma de suas formulações "oficiais": a

entropia de um sistema fechado não pode diminuir.

Agora isso é menos como uma tautologia, certo? Mas que tipo de palavra inteligente é entropia?

Vamos imaginar o ar enchendo uma sala. Consiste em um grande número de moléculas. Se dividirmos mentalmente a sala em células, obteremos um análogo tridimensional do jogo de pedras em um tabuleiro muito grande com um grande número de pedras. Cada posição do jogo, neste caso, é chamada de macroestado do sistema. Cada um dos layouts de pedras que implementam uma posição específica é um microestado . Tomamos dois números: o número de todos os microestados que realizam esse macroestado e o número de todos os microestados possíveis. Se dividirmos o primeiro no segundo, obteremos a probabilidade desse macroestado.

Definição do livro: a entropia do estado de um sistema é o logaritmo da probabilidade desse estado.

Nós o traduzimos para um idioma que Grant entende - a entropia de uma posição é o logaritmo do peso de uma determinada posição. Vamos tentar deixar isso ainda mais claro: quanto mais maneiras você conseguir uma posição, mais entropia.

Agora, vemos que a formulação do livro do segundo princípio diz o seguinte: de uma posição em si, apenas uma transição para uma posição que pode ser obtida em mais ou com o mesmo número de caminhos que o inicial pode ocorrer.

Vamos tentar simplificá-lo: se abalarmos o quadro, chegaremos mais cedo a uma posição mais fácil.

Parece que voltamos à tautologia. No entanto, mesmo que seja uma tautologia, o segundo princípio é uma das leis físicas mais importantes. Além disso, esta é a única lei da física que nos diz que o tempo deve fluir em uma determinada direção, o que faz a diferença entre o passado e o futuro.

Finalmente, vamos ver mais algumas formulações do segundo começo:

• Postulado de Clausius: Um processo circular é impossível, cujo único resultado é a transferência de calor de um corpo menos aquecido para um mais quente
• Postulado de Thomson: Um processo circular é impossível, cujo único resultado seria a produção de trabalho pelo resfriamento do reservatório de calor.

Como você pode ver, não há mais uma tautologia. E nenhum deles é óbvio. No entanto, pode ser demonstrado que ambas as formulações são completamente equivalentes às tautológicas "é mais provável que algo mais provável aconteça". Às vezes, para aprender algo novo, precisamos primeiro tomar consciência de algo óbvio.

Na próxima parte, consideraremos outra "tautologia científica" que, à primeira vista, viola a segunda lei da termodinâmica.

Source: https://habr.com/ru/post/pt400803/