Professor de matemática quer derrotar o jerrymandering através da ciência

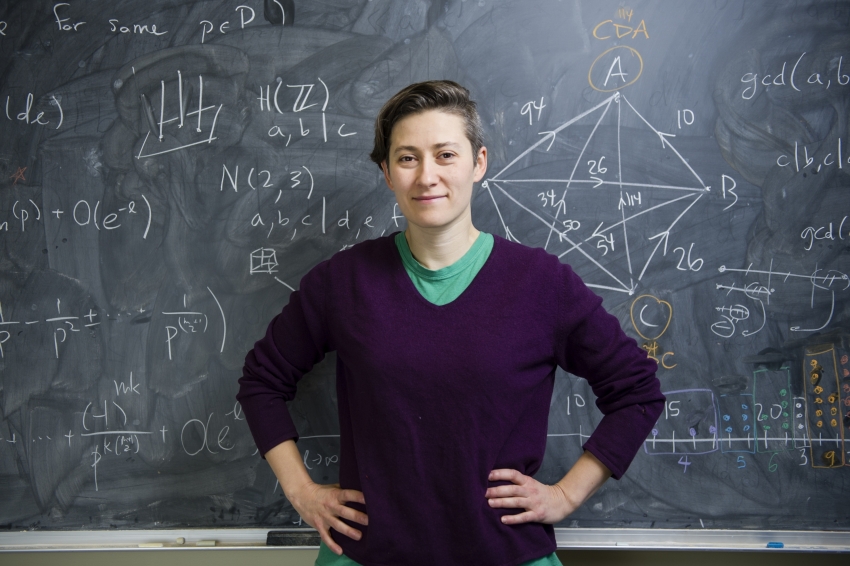Moon Duchin, professor associado de matemática e diretor do programa de ciência, tecnologia e sociedade da Universidade Tufts (EUA).

Partidos políticos e comissões eleitorais nos EUA, Rússia e outros países tradicionalmente “trapaceiam” com o tamanho e a forma dos constituintes, tentando isolar a parte de protesto do eleitorado em reservas separadas ou, inversamente, uma pequena mancha nos distritos vizinhos. Devido a essas manipulações - jerrymandering -, os distritos às vezes adquirem contornos muito bizarros. Mas tudo é legal. Até agora, não há legislação normal com fórmulas matemáticas que descrevem a forma geométrica do distrito. O professor associado de matemática da Universidade Tufts pretende corrigir essa falha e oferece vários modelos matemáticos.

Jerrymandering é freqüentemente usado em países com eleições parlamentares majoritárias e um sistema partidário forte. Para que o número máximo de deputados “próprios” chegue ao parlamento, os eleitores do partido da oposição estão concentrados em vários círculos eleitorais, enquanto no restante eles fazem uma pequena, mas confiante, vantagem para o seu partido. É por isso que os eleitorados são criados com um número desigual de eleitores, assim como eleitorados de uma forma territorial bizarra.

Por exemplo, nos Estados Unidos, o jerrymandering foi usado para neutralizar os eleitores negros, para que seus candidatos não fossem ao parlamento (houve casos de discriminação positiva quando foram os candidatos negros que foram promovidos dessa maneira). E na Rússia, em 2015, antes das eleições parlamentares, uma lei foi adotada sobre o corte "de pétalas" dos distritosem que pequenos setores de grandes cidades com eleitores desleais se unem a grandes territórios rurais com uma população leal. Como resultado, o jerrymandering realiza a mesma tarefa - bloqueia a passagem de candidatos "maliciosos" ao parlamento na maioria dos distritos.

Por exemplo, na região de Novosibirsk, as autoridades dividiram a população da cidade em quatro partes e anexaram cada uma delas ao território da região.


Distritos eleitorais da região de Novosibirsk

Nos Estados Unidos, a situação com a jerrymandering é ainda pior, porque na maioria dos estados, o corte de distritos é de responsabilidade dos parlamentos regionais (que, de fato, está nas mãos do partido com maioria parlamentar). Por exemplo, a região de Novosibirsk nem sequer está perto em seu grau de idiotice da distribuição de Maryland em oito municípios.


Pcs segundo distrito.


Distrito três de Maryland Maryland

Nesse caso, as constituições estaduais geralmente fornecem apenas regras básicas na forma de constituintes ou nenhuma regra. Geralmente, é indicado que o distrito deve ser "compacto", mas essa é claramente uma afirmação ampla e subjetiva.

Para mudar a situação, Moon Dachin criou uma organização especializada de cinco membros, o Metric Geometry and Gerrymandering Group (MGGG), que abriu uma lista de discussão para começar a discutir o problema do jerrymandering na comunidade científica. Ela descreveu os objetivos da organização em entrevista à revista Chronicle of Higher Education.

O que é compacidade?

O professor associado Dachin propõe considerar a possibilidade de usar vários conceitos para descrever a forma aceitável do distrito, ou seja, verificar objetivamente o requisito de "compacidade", que está escrito nas constituições estaduais.

Por exemplo, você pode considerar um parâmetro como a pontuação de Polsby-Popper , calculada como a proporção da área de um município com a área de um círculo cujo comprimento é igual ao perímetro do município.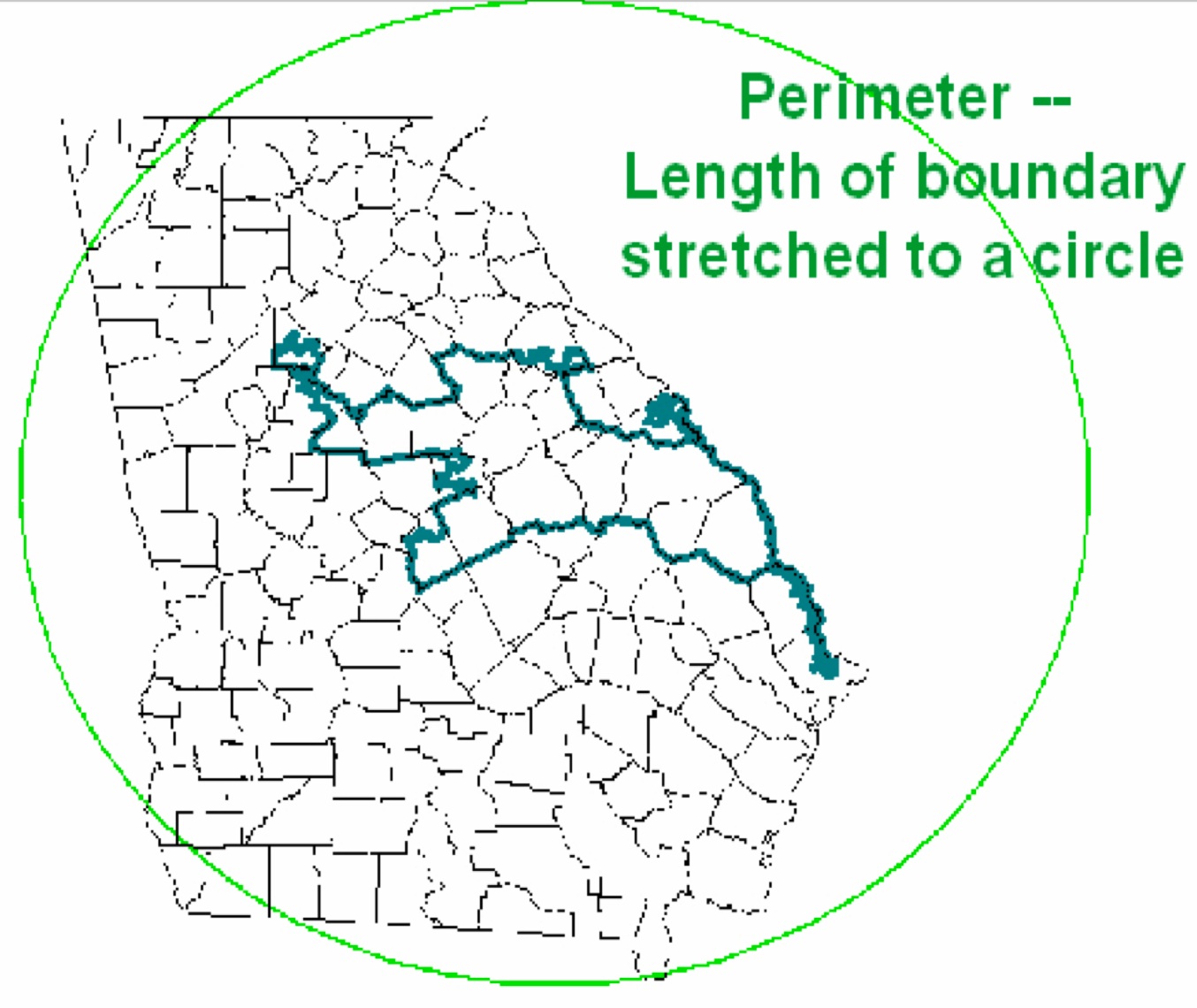


Estimativa de Polsby-Popper

Outra opção é uma proporção simples da área do município para a área do círculo no círculo circunscrito.


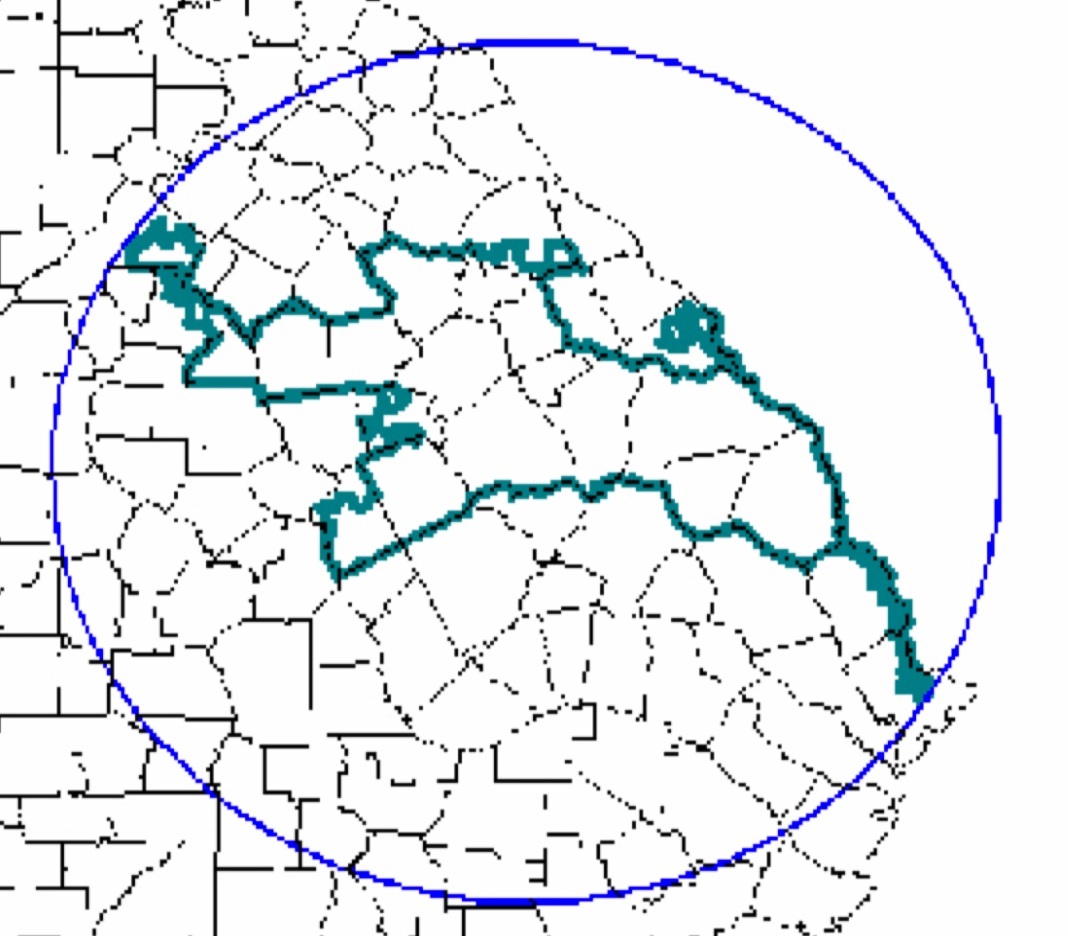A proporção da área do distrito para a área do círculo

Moon Dachin diz que agora está trabalhando em problemas de geometria métrica no quadro da teoria geométrica de grupos. Este é um campo da matemática que estuda grupos finitamente gerados usando as conexões entre suas propriedades algébricas e as propriedades topológicas e geométricas dos espaços em que esses grupos atuam, ou dos próprios grupos, considerados objetos geométricos. No site pessoal de Danchin , você pode encontrar vários trabalhos científicos nessa área, nos quais ela descreve um parâmetro como a distância média entre todos os pontos de uma figura arbitrária (provavelmente, o parâmetro ainda precisa ser normalizado, por exemplo, pelo diâmetro do mesmo círculo descrito). Este parâmetro é bastante adequado como uma característica da compactação.

Outra opção para avaliar a compacidade, que os especialistas mencionam brincando- O teste interocular de Grofman, proposto pelo cientista americano Bernie Grofman. Esse teste permite determinar visualmente o nível de gerrymandering, medindo a largura dos olhos de uma pessoa, que está olhando o mapa e avaliando a escala de fraude. A propósito, o mesmo teste já foi oferecido para avaliar o pornô "hardcore". A questão é que é difícil formalizar essas coisas, mas quando você a vê, entende imediatamente (olhe novamente para os condados de Maryland).

O professor associado da Tufts University está confiante de que, com a ajuda da matemática, muitos problemas sociais podem ser resolvidos. Mas a dificuldade é que os políticos geralmente não conseguem entender conceitos matemáticos simples. Portanto, será bastante difícil convencê-los a introduzir tais fórmulas nas leis e na Constituição do país. Afinal, eles devem primeiro ser entendidos. Moon Dachin dá um exemplo do conceito de falta de eficiência , que descreve Jerrymandering com exemplos simples - um caso único em que um juiz dos EUA entendeu a matemática e disse que "gostava" dela. Este documento matemático formou a base do Whitford v. Nichol em Wisconsin. É assim que os conceitos matemáticos devem ser explicados e apresentados aos juízes, políticos e sociedade: o mais claro e convincente possível.

Source: https://habr.com/ru/post/pt401851/