Entrelaçamento quântico sem confusão - o que é isso

1. Introdução

Apareceram muitos artigos populares que falam sobre emaranhamento quântico. Experimentos com entrelaçamento quântico são espetaculares, mas não recebem prêmios. Por que experimentos tão interessantes para o leigo não interessam aos cientistas? Artigos populares falam sobre as propriedades surpreendentes de pares de partículas emaranhadas - a exposição a uma leva a uma mudança instantânea no estado da segunda. E o que está oculto por trás do termo "teletransporte quântico", sobre o qual eles já começaram a dizer que está acontecendo em velocidade superluminal. Vejamos tudo isso do ponto de vista da mecânica quântica normal.

O que vem da mecânica quântica

As partículas quânticas podem estar em dois tipos de estados, de acordo com o livro clássico de Landau e Lifshitz - puro e misto. Se uma partícula não interage com outras partículas quânticas, é descrita por uma função de onda que depende apenas de suas coordenadas ou momento - esse estado é chamado de puro. Nesse caso, a função de onda obedece à equação de Schrödinger. Outra opção é possível - a partícula interage com outras partículas quânticas. Nesse caso, a função de onda já se refere a todo o sistema de partículas em interação e depende de todas as suas variáveis ​​dinâmicas. Se estivermos interessados ​​em apenas uma partícula, seu estado, como Landau mostrou há 90 anos, pode ser descrito por um operador de matriz ou densidade. A matriz de densidade obedece a uma equação semelhante à equação de Schrödinger



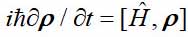
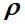
onde É a matriz de densidade, H é o operador Hamilton e os colchetes indicam o comutador.

Landau o trouxe para fora. Quaisquer quantidades físicas relacionadas a uma determinada partícula podem ser expressas através de uma matriz de densidade. Essa condição é chamada mista. Se temos um sistema de partículas interagindo, então cada uma delas está em um estado misto. Se as partículas se espalharem por grandes distâncias e a interação desaparecer, seu estado ainda permanecerá misturado. Se cada uma das várias partículas estiver em estado puro, a função de onda de um sistema desse tipo é o produto das funções de onda de cada uma das partículas (se as partículas forem diferentes. Para partículas idênticas, bósons ou férmions, é necessário compor uma combinação simétrica ou anti-simétrica, consulte [1], mas depois, a identidade de partículas, férmions e bósons já é uma teoria quântica relativística.

Um estado emaranhado de um par de partículas é um estado no qual existe uma correlação constante entre quantidades físicas relacionadas a diferentes partículas. Um exemplo simples e mais comum é uma certa quantidade física total, por exemplo, a rotação total ou o momento angular de um par. Um par de partículas está em um estado puro, mas cada uma delas está em um estado misto. Pode parecer que uma mudança no estado de uma partícula afetará imediatamente o estado de outra partícula. Mesmo que eles se espalhem para longe e não interajam, é isso que se expressa em artigos populares. Esse fenômeno já foi chamado de teletransporte quântico, e alguns jornalistas analfabetos afirmam que a mudança ocorre instantaneamente, ou seja, se propaga mais rápido que a velocidade da luz.

Considere isso do ponto de vista da mecânica quântica: primeiro, qualquer ação ou medida que altere o momento de rotação ou momento angular de apenas uma partícula viola imediatamente a lei de conservação da característica total. O operador correspondente não pode comutar com rotação completa ou momento angular total. Assim, o emaranhamento inicial do estado de um par de partículas é violado. A rotação ou o momento da segunda partícula não pode mais ser inequivocamente associado à da primeira partícula. Você pode considerar esse problema do outro lado. Após o desaparecimento da interação entre as partículas, a evolução da matriz de densidade de cada uma das partículas é descrita por sua própria equação, na qual as variáveis ​​dinâmicas das outras partículas não são incluídas. Portanto, a exposição a uma partícula não altera a matriz de densidade para outra.

Existe até o teorema de Eberhard [2], que afirma que a influência mútua de duas partículas não pode ser detectada por medições. Haja um sistema quântico, que é descrito por uma matriz de densidade. E deixe esse sistema consistir em dois subsistemas A e B. O teorema de Eberhard afirma que nenhuma medição de observáveis ​​relacionados apenas ao subsistema A não afeta o resultado da medição de quaisquer observáveis ​​relacionados apenas ao subsistema B. No entanto, a prova do teorema usa a hipótese de redução de ondas uma função que não foi provada nem teoricamente nem experimentalmente. Mas todas essas considerações são feitas dentro da estrutura da mecânica quântica não-relativística e se relacionam com várias partículas não idênticas.

Essas considerações não funcionam na teoria relativística no caso de um par de partículas idênticas. Deixe-me lembrá-lo mais uma vez que a identidade ou indistinguibilidade das partículas vem da mecânica quântica relativística, onde o número de partículas não é preservado. No entanto, para partículas lentas, podemos usar um aparato mais simples da mecânica quântica não-relativística, simplesmente levando em consideração a indistinguibilidade das partículas. Então a função de onda do par deve ser simétrica (para bósons) ou anti-simétrica (para férmions) com relação à permutação das partículas. Tal requisito surge na teoria relativística, independentemente da velocidade das partículas. É esse requisito que leva a correlações de longo alcance de um par de partículas idênticas. Em princípio, um próton com um elétron também pode estar em um estado emaranhado. No entanto, se eles se dispersarem por várias dezenas de angstroms, a interação com os campos eletromagnéticos e outras partículas destruirá esse estado. A interação de troca (como esse fenômeno é chamado) atua a distâncias macroscópicas, como mostram os experimentos. Um par de partículas, mesmo dispersas por metros, permanece indistinguível. Se você está fazendo uma medição, não sabe exatamente a que partícula o valor medido pertence. Você está fazendo medições com um par de partículas ao mesmo tempo. Portanto, todas as experiências espetaculares foram realizadas exatamente com as mesmas partículas - elétrons e fótons. A rigor, esse não é o estado confuso considerado na estrutura da mecânica quântica não-relativística, mas algo semelhante.

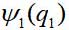
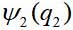
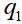
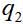
Considere o caso mais simples - um par de partículas idênticas que não interagem. Se as velocidades são pequenas, podemos usar a mecânica quântica não-relativística, levando em consideração a simetria da função de onda em relação à permutação de partículas. Deixe a função de onda da primeira partícula , a segunda partícula - onde e - variáveis ​​dinâmicas da primeira e segunda partículas, no caso mais simples - apenas as coordenadas. Então a função de onda do par



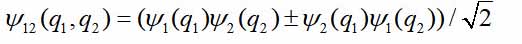
Os sinais + e - referem-se a bósons e férmions. Suponha que as partículas estejam afastadas. Então localizados nas áreas remotas 1 e 2, respectivamente, ou seja, fora dessas áreas são pequenos. Vamos tentar calcular o valor médio de alguma variável da primeira partícula, por exemplo, a coordenada. Para simplificar, podemos imaginar que apenas coordenadas são incluídas nas funções de onda. Acontece que o valor médio das coordenadas da partícula 1 está entre as regiões 1 e 2 e coincide com o valor médio da partícula 2. Isso é realmente natural - as partículas são indistinguíveis, não podemos saber qual partícula as coordenadas são medidas. Em geral, todos os valores médios para as partículas 1 e 2 serão os mesmos. Isso significa que, movendo a região de localização da partícula 1 (por exemplo, a partícula está localizada dentro do defeito da estrutura cristalina e movemos o cristal inteiro), agimos na partícula 2, embora as partículas não interajam no sentido usual - através de um campo eletromagnético, por exemplo. Este é um exemplo simples de emaranhamento relativístico.

Nenhuma transferência instantânea de informações devido a essas correlações entre as duas partículas ocorre. O aparato da teoria quântica relativística foi originalmente construído para que eventos no espaço-tempo em lados opostos do cone de luz não possam se influenciar. Simplificando, nenhum sinal, nenhuma influência ou perturbação pode se propagar mais rápido que a luz. Ambas as partículas são na verdade o estado de um campo, por exemplo, elétron-pósitron. Ao agir no campo em um ponto (na partícula 1), criamos um distúrbio que se propaga como ondas de água. Na mecânica quântica não-relativística, a velocidade da luz é considerada infinitamente grande, o que cria a ilusão de mudança instantânea.

A situação em que as partículas espaçadas por longas distâncias permanecem acopladas aos pares parece paradoxal devido às idéias clássicas sobre partículas. Devemos lembrar que, na realidade, não existem partículas, mas campos. O que representamos como partículas é simplesmente o estado desses campos. A idéia clássica de partículas é completamente inadequada no microworld. Imediatamente surgem perguntas sobre o tamanho, forma, material e estrutura das partículas elementares. De fato, situações paradoxais para o pensamento clássico surgem com uma partícula. Por exemplo, no experimento de Stern-Gerlach, um átomo de hidrogênio voa através de um campo magnético não homogêneo direcionado perpendicularmente à velocidade. O spin do núcleo pode ser negligenciado devido à pequenez do magneton nuclear; deixe o spin do elétron ser inicialmente direcionado ao longo da velocidade.



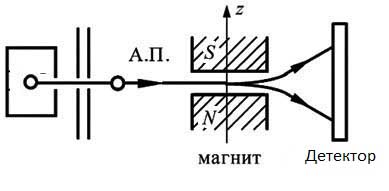
A evolução da função de onda atômica é fácil de calcular. O pacote de ondas localizado inicial é dividido em dois idênticos, voando simetricamente em um ângulo com a direção original. Ou seja, um átomo, uma partícula pesada, geralmente considerada clássica com uma trajetória clássica, dividida em dois pacotes de ondas que podem se espalhar a distâncias macroscópicas completamente. Ao mesmo tempo, observo - resulta do cálculo que mesmo um experimento ideal de Stern-Gerlach não é capaz de medir a rotação de partículas.

Se o detector ligar um átomo de hidrogênio, por exemplo, quimicamente, as “metades” - dois pacotes de ondas dispersas são reunidas em uma. Como ocorre essa localização da partícula manchada é uma teoria existente separadamente, na qual eu não entendo. Os interessados ​​podem encontrar extensa literatura sobre esse assunto.

Conclusão

Surge a questão - qual é o sentido de inúmeras experiências em demonstrar correlações entre partículas a grandes distâncias? Além de confirmar a mecânica quântica, que nenhum físico normal duvida há muito tempo, esta é uma demonstração espetacular que impressiona os funcionários públicos e amadores que alocam fundos para a ciência (por exemplo, o Gazprombank patrocina o desenvolvimento de linhas de comunicação quântica). Para a física, essas demonstrações caras não dão nada, embora permitam o desenvolvimento de técnicas experimentais.

Literatura
1. Landau, L. D., Lifshits, E. M. Mecânica quântica (teoria não-relativística). - 3ª edição, revisada e complementada. - M.: Nauka, 1974. - 752 p. - ("Física Teórica", Volume III).
2. Eberhard, PH, "Teorema de Bell e os diferentes conceitos de não-localidade", Nuovo Cimento 46B, 392-419 (1978)