“Existem duas bolas idênticas na mesma temperatura. Um deles fica em uma superfície horizontal, o outro está suspenso em um fio. Ambas as bolas relatam a mesma quantidade de calor. As bolas serão as mesmas depois disso ou não? (Qualquer tipo de perda de calor pode ser negligenciada.) "

Às vezes, esse problema pode ser encontrado nas olimpíadas de física e mídia social . A resposta geralmente aceita é intuitiva: devido à energia gasta na expansão térmica na presença de gravidade, uma bola posicionada em uma superfície horizontal será mais fria do que pendurada em um fio. Um artigo recente mostrou que esta resposta está incorreta. De fato, o resultado será o oposto: a bola mentirosa será mais quente que a bola pendurada. Vamos entender por que o método tradicional de resolver esse problema leva à resposta errada e por que a intuição nesse caso nos derruba.

Solução tradicional e seu problema

A solução tradicional é baseada na seguinte linha de raciocínio. Ambas as bolas se expandirão durante o aquecimento, por causa disso o centro de massa da bola deitado em uma superfície horizontal aumentará levemente e o centro de massa da bola pendurada cairá. Como resultado, a bola mentirosa esquenta mais, pois parte do calor transferido para ela é gasto em sua ascensão, e a bola suspensa esquenta mais devido ao trabalho adicional da gravidade quando é abaixada.


Raciocínio usado na solução tradicional: devido à expansão térmica, a bola colocada na mesa sobe e a bola pendurada no fio é abaixada.

A resposta pode ser expressa por uma fórmula simples para a diferença de temperatura ( $$ ) e pendurado ( $$ ) bolas:

$$

onde $$ , $$ e $$ - massa, raio e capacidade de aquecimento das bolas, $$ - a quantidade de calor transferida para eles, $$ - aceleração da gravidade, $$ É o coeficiente de expansão térmica linear do material das bolas, que consideramos suficientemente pequeno. Como visto $$ - a bola mentirosa será mais fria.

Parece que nesta decisão tudo é lógico. A “primeira andorinha”, demonstrando que algo está errado aqui, é uma tentativa mental de criar um motor térmico com base na bola.

A máquina pode funcionar da seguinte maneira: primeiro, a bola fica sobre a mesa, onde a aquecemos, por causa da qual seu centro de massa se eleva. Em seguida, fixamos a bola no fio pendurado em cima e removemos cuidadosamente a mesa para que a altura da bola não mude. Finalmente, resfriamos a bola à sua temperatura inicial, como resultado, a bola é comprimida e seu centro de massa aumenta. Conclusão: a parte do calor que transferimos para a bola quando foi aquecida se transformou em trabalho mecânico para aumentá-la, e esse ciclo pode ser repetido infinitamente.


O ciclo de operação de um motor térmico baseado em bola: após aquecimento e resfriamento, a bola subia, o que significa que transformamos parte do calor em trabalho mecânico.

O problema aqui é que, aumentando o raio da bola, a eficiência (eficiência) de uma máquina desse tipo pode ser feita arbitrariamente perto de 100%. Isso contradiz a segunda lei da termodinâmica , segundo a qual a eficiência de um motor térmico não pode exceder a eficiência do ciclo de Carnot nas mesmas temperaturas do aquecedor e da geladeira.

Qual é o problema?

Por que a solução tradicional para o problema está errada? Aqui é necessário levar em consideração que a bola que está sobre a mesa desde o início, antes de ser aquecida, será levemente achatada pela gravidade e a bola pendurada será levemente esticada. Isso afetará negativamente a eficiência do mecanismo térmico acima descrito: durante a suspensão, a bola diminuirá levemente, por isso a eficiência diminuirá e não excederá mais a eficiência do ciclo de Carnot.


O efeito da gravidade nas bolas: a bola sobre a mesa é achatada e a que está pendurada no fio é esticada.

Como isso se manifestará ao considerar o problema original? Acontece que comprimir ou esticar um material altera sua capacidade de aquecimento: no caso de um material comprimido, o aquecimento para a mesma temperatura exigirá menos calor do que no caso de um material esticado. Portanto:

• Quando a bola sobre a mesa é aquecida, parte do calor aumenta devido à expansão térmica; mas, junto com isso, o aquecimento do próprio material da bola será mais fácil e exigirá menos calor.
• Quando uma bola pendurada em um fio é aquecida, o trabalho de gravidade quando é abaixado será adicionado ao calor transferido para ele; mas, junto com isso, o aquecimento do próprio material da bola consumirá mais tempo e exigirá mais calor.

Na solução tradicional, apenas os fatores indicados pelas setas brancas são levados em consideração. Ignorar os fatores mostrados pelas setas pretas leva a uma resposta incorreta.

Como podemos ver, em ambos os casos, existem fatores que funcionam tanto a favor de uma resposta (a bola mentirosa pode ser mais fria quanto a pendurada) e na direção oposta (a bola mentirosa pode se mostrar mais quente que a pendurada). Qual deles domina?

Parece que o efeito de alterar a capacidade de calor de um material durante a compressão ou tensão, mesmo que exista, deve ser muito pequeno e pode ser negligenciado, como é feito na solução tradicional do problema. No entanto, isso não é verdade. Esse efeito é da mesma ordem de pequenez que a própria expansão térmica, uma vez que esses dois efeitos decorrem da anarmonicidade das forças interatômicas. Levar um desses efeitos em consideração na solução tradicional combinada com ignorar o outro é inconsistente e leva a uma resposta incorreta.

O artigo mostra que, com a solução correta para o problema, a diferença de temperatura das bolas após transferir a mesma quantidade de calor para elas é igual a:

$$

onde $$ - a temperatura absoluta das bolas, $$ - a taxa de variação do coeficiente de expansão térmica do material das bolas com uma mudança de temperatura.

Comparado com o resultado da solução tradicional, a diferença de temperatura é:

• O sinal oposto, pois para a maioria dos materiais o valor $$ é positivo, portanto todo o lado direito da igualdade também é positivo, e $$ .
• Muito menor em valor absoluto, pois aqui, em vez de um valor pequeno, aparecem valores ainda menores $$ e $$ .

Assim, os dois efeitos discutidos acima se cancelam quase completamente, mas o segundo deles (mudança na capacidade de calor durante a compressão ou tensão) é um pouco mais forte que o primeiro (expansão térmica).

Anarmonicidade de forças interatômicas

Os autores do artigo realizam uma consideração bastante rigorosa do problema, mas, infelizmente, não fornecem uma explicação clara de como exatamente ocorre a compensação quase completa dos dois efeitos, então eu mesmo tive que descobrir isso.

A figura mostra uma dependência típica da energia potencial da interação atômica com a distância entre eles. A força que atua sobre os átomos é direcionada para uma diminuição da energia potencial; portanto, os átomos se repelem fortemente a pequenas distâncias e são atraídos fracamente a grandes distâncias. A alguma distância $$ energia potencial atinge um mínimo. O desejo dos átomos a essa distância mais vantajosa em termos energéticos é a razão de sua ligação a moléculas, líquidos e sólidos.


Agora vamos ver de onde vem a expansão térmica dos materiais. No movimento térmico caótico, a distância entre os átomos não é mais estritamente igual $$ e flutua próximo a esse valor. A ligação entre os átomos tem a propriedade do anarmonismo: ela se comporta como uma mola assimétrica, mais fácil de esticar do que comprimir. Como resultado, durante o movimento térmico, a ligação é esticada na maioria das vezes, não compactada, portanto a distância média $$ entre átomos se torna mais do que $$ . Com o aumento da temperatura, esse efeito se intensifica, as distâncias entre os átomos aumentam e o material se expande.


O motivo da expansão térmica dos materiais: durante o movimento térmico, a distância média entre os átomos aumenta devido à anarmonicidade das forças de interação interatômica.

O que acontece quando o material é comprimido ou esticado, como no caso de bolas achatadas ou esticadas? Quando um material é comprimido, uma força externa diminui a distância média entre átomos e, quando esticada, aumenta.


Sob compressão, a distância de equilíbrio entre os átomos diminui, enquanto sob tensão aumenta.

Agora estamos prontos para entender como a compressão e a tensão de um material afetam sua capacidade de aquecimento. Imagine que apertamos o material, de modo que a distância entre os átomos durante o movimento térmico agora oscila perto da posição de equilíbrio deslocada para a esquerda. Nesse caso, o anarmonismo não desapareceu, portanto, como antes, quando aquecido, a distância média entre os átomos aumentará. Mas, ao mesmo tempo, voltaremos ao mínimo de energia potencial, o que significa que a energia do material diminuirá ainda mais! Isso explica a diminuição da capacidade de calor do material durante a compressão: a expansão térmica leva a uma pequena redução adicional na energia das interações interatômicas, portanto, é necessária menos energia para aquecer o material.



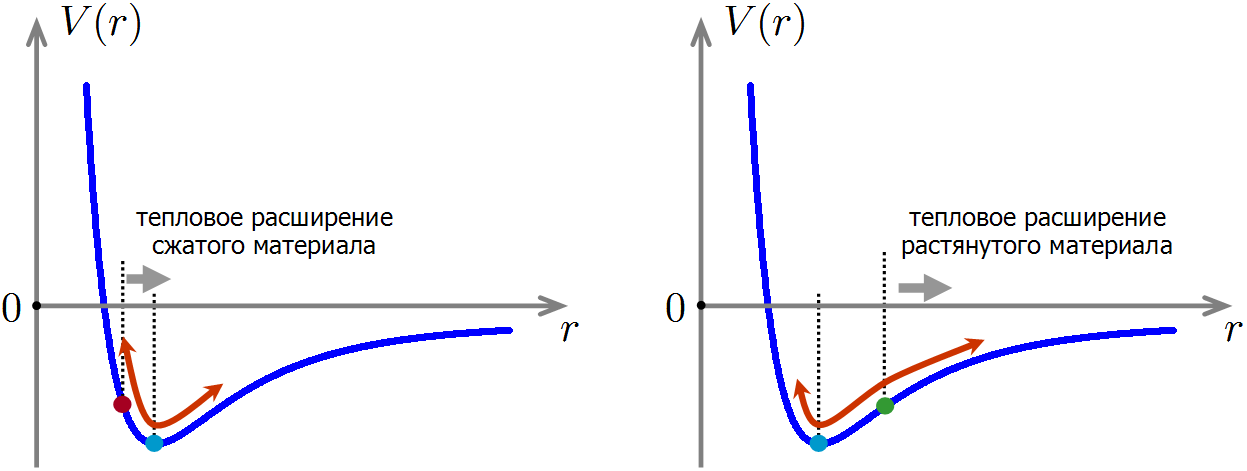
Se o material é esticado, a situação é oposta: com a expansão térmica, a energia de interação dos átomos crescerá mais rapidamente do que no material não esticado. Portanto, para aquecer o material esticado na mesma temperatura, é necessário um pouco mais de energia do que sem esticar, o que significa que a capacidade de calor do material esticado será maior.

Assim, no exemplo do problema das olimpíadas, que por muitas décadas foi resolvido (e talvez continue a ser resolvido) erroneamente, vemos que a física real às vezes contradiz nossa intuição. Portanto, é tão importante na resolução de problemas o uso cuidadoso do aparato matemático, não limitado ao raciocínio superficial.

De acordo com o artigo :

Giacomo De Palma, Mattia C. Sormani, Efeito contra-intuitivo da gravidade na capacidade térmica de uma esfera sólida: reexame de um problema bem conhecido, American Journal of Physics 83, 723 (2015).
Pré-impressão pública do artigo: arxiv.org/pdf/1502.01337