Característica de fluxo linearizado de uma turbina a vapor. Parte 2. Exemplo de construção da turbina PT-80 no MATLAB

Prefácio da primeira parte

Modelar turbinas a vapor é uma tarefa diária para centenas de pessoas em nosso país. Em vez da palavra modelo, é costume dizer uma característica de despesa . As características de consumo das turbinas a vapor são usadas na solução de problemas como o cálculo do consumo específico de combustível equivalente para eletricidade e calor produzido pelas usinas termelétricas; otimização do CHP; planejamento e manutenção de modos de usinas termelétricas.

Eu desenvolvi uma nova característica de fluxo de uma turbina a vapor - uma característica de fluxo linearizado de uma turbina a vapor. A característica de fluxo desenvolvida é conveniente e eficaz na solução desses problemas. No entanto, no momento, é descrito apenas em dois trabalhos científicos:

1. Otimização da operação de usinas termelétricas nas condições do mercado atacadista de energia elétrica e capacidade da Rússia ;
2. Métodos computacionais para determinar o consumo específico de combustível equivalente de usinas termelétricas para a energia elétrica e térmica fornecida no modo de geração combinada .

E agora no meu blog eu gostaria de:

• primeiro, em uma linguagem simples e acessível para responder às perguntas básicas sobre a nova característica de vazão (consulte. Característica de vazão linearizada de uma turbina a vapor. Parte 1. Perguntas básicas );
• segundo, forneça um exemplo de construção de uma nova característica de fluxo que ajude a entender o método de construção e as propriedades da característica (veja abaixo);
  
• em terceiro lugar, refutar duas declarações bem conhecidas sobre os modos de operação de uma turbina a vapor (consulte. Características de fluxo linearizado de uma turbina a vapor. Parte 3. Dispersando mitos sobre a operação de uma turbina a vapor ).
  

1. Os dados de origem

Os dados iniciais para a construção de uma característica de fluxo linearizado podem ser

1. valores de potência reais Q ₀ , N, Q _p , Q _t medidos durante a operação da turbina a vapor,
2. nomogramas q _t brutos da documentação normativa e técnica.

Obviamente, os valores instantâneos reais de Q ₀ , N, Q _p , Q _t são dados de fonte ideais. A coleta desses dados é demorada.

Nos casos em que os valores reais de Q ₀ , N, Q _p , Q _t não _estão disponíveis, é possível processar nomogramas q _t brutos. Eles, por sua vez, foram obtidos com base em medições. Leia mais sobre testes de turbinas em VM Gornstein e outros métodos para otimizar os modos de sistemas de energia .

2. O algoritmo para construir características de fluxo linearizadas

O algoritmo de construção consiste em três etapas.

1. Tradução de nomogramas ou resultados de medidas em uma exibição tabular.
2. Linearização da característica de fluxo de uma turbina a vapor.
3. Determinação dos limites da faixa de controle da turbina a vapor.

Ao trabalhar com nomogramas q _t bruto, o primeiro passo é rápido. Este trabalho é chamado de digitalização . A digitalização de 9 nomogramas para o exemplo atual levou cerca de 40 minutos.

A segunda e terceira etapas requerem o uso de pacotes matemáticos. Eu amo e uso o MATLAB por muitos anos. Meu exemplo de construção de uma característica de fluxo linearizado é feito nela. É possível fazer o download de um exemplo no link , executar e descobrir independentemente o método de construção de uma característica de fluxo linearizado.

A característica de fluxo da turbina em questão foi construída para os seguintes valores fixos dos parâmetros de modo:

• operação de estágio único
• pressão média do vapor = 13 kgf / cm2,
• pressão de vapor de baixa pressão = 1 kgf / cm2.

Conteúdo do arquivo Chuchueva-PT-80-característica-linear-curva.rar .

1) Nomogramas de consumo específico brutos qt para geração de eletricidade (pontos vermelhos marcados são digitalizados - transferidos para a tabela):

• PT80_qt_Qm_eq_0_digit.png,
• PT80_qt_Qm_eq_100_digit.png,
• PT80_qt_Qm_eq_120_digit.png,
• PT80_qt_Qm_eq_140_digit.png,
• PT80_qt_Qm_eq_150_digit.png,
• PT80_qt_Qm_eq_20_digit.png,
• PT80_qt_Qm_eq_40_digit.png,
• PT80_qt_Qm_eq_60_digit.png,
• PT80_qt_Qm_eq_80_digit.png.

2) O resultado da digitalização (cada arquivo csv corresponde a um arquivo png):

• PT-80_Qm_eq_0.csv,
• PT-80_Qm_eq_100.csv,
• PT-80_Qm_eq_120.csv,
• PT-80_Qm_eq_140.csv,
• PT-80_Qm_eq_150.csv,
• PT-80_Qm_eq_20.csv,
• PT-80_Qm_eq_40.csv,
• PT-80_Qm_eq_60.csv,
• PT-80_Qm_eq_80.csv.

3) Script MATLAB com cálculos e gráficos:

• PT_80_linear_characteristic_curve.m

4) O resultado da digitalização dos nomogramas e o resultado da construção de uma característica de fluxo linearizada em forma de tabela:

• PT_80_linear_characteristic_curve.xlsx.

Etapa 1. Tradução de nomogramas ou resultados de medidas em uma exibição tabular

1. Processamento de dados de origem

Os dados iniciais para o nosso exemplo são nomogramas q _t brutos.

Para digitalizar muitos nomogramas, você precisa de uma ferramenta especial. Eu tenho usado repetidamente um aplicativo da web para esses fins. O aplicativo é simples, conveniente, mas não possui flexibilidade suficiente para automatizar o processo. Parte do trabalho deve ser feita manualmente.

Nesta etapa, é importante digitalizar os pontos extremos dos nomogramas que definem os limites da faixa de ajuste da turbina a vapor .

O trabalho era marcar os pontos da característica de descarga em cada arquivo png usando o aplicativo , fazer o download do csv resultante e coletar todos os dados em uma tabela. O resultado da digitalização pode ser encontrado no arquivo PT-80-característica-linear-curva.xlsx, folha “PT-80”, tabela “Dados de entrada”.

2. Trazendo unidades de medida para unidades de potência

A seguir, na planilha "PT-80" calculamos os valores de Q _{0 de} acordo com a fórmula

$$$$ display $$ \ begin {equação} Q_0 = \ frac {q_T \ cdot N} {1000} + Q_P + Q_T \ qquad (1) \ end {equação} $$ display $$

e trazemos todos os valores iniciais para MW. Os cálculos são implementados usando o MS Excel.

A tabela resultante “Dados de entrada (potência da unidade)” é o resultado da primeira etapa do algoritmo.

Etapa 2. Linearização da característica de fluxo da turbina a vapor

1. Teste do MATLAB

Nesta etapa, você precisa instalar e abrir a versão do MATLAB não inferior a 7.3 (esta é uma versão antiga, atual 8.0). No MATLAB, abra o arquivo PT_80_linear_characteristic_curve.m, execute-o e verifique se está funcionando. Tudo funciona corretamente, se após os resultados da execução do script na linha de comando, você vir a seguinte mensagem:

    PT_80_linear_characteristic_curve.xlsx  1  : a(N) = 2.317, a(Q) = 0.621, a(Q) = 0.255, a0 = 33.874   = 0.006, (0.57%)      = 37 

Se você tiver algum erro, descubra como corrigi-lo.

2. Cálculos

Todos os cálculos são implementados no arquivo PT_80_linear_characteristic_curve.m. Vamos considerar em partes.

1) Indicamos o nome do arquivo de origem, a planilha, o intervalo de células que contém a tabela “Dados de origem (unidade de capacidade)” obtida na etapa anterior.

 XLSFileName = 'PT_80_linear_characteristic_curve.xlsx'; XLSSheetName = 'PT-80'; XLSRange = 'F3:I334'; 

2) Lemos os dados de origem no MATLAB.

 sourceData = xlsread(XLSFileName, XLSSheetName, XLSRange); N = sourceData(:,1); Qm = sourceData(:,2); Ql = sourceData(:,3); Q0 = sourceData(:,4); fprintf('    %s  %1.0f \n', XLSFileName, toc); 

Usamos a variável Qm para a vazão média do vapor Q _p , o índice m do meio é médio; Da mesma forma, usamos a variável Ql para fluxo de vapor de baixa pressão Qn, o índice l de baixo é baixo.

3) Defina os coeficientes α _i .

Lembre-se da fórmula geral para as características de fluxo

$$$$ display $$ \ begin {equação} Q_0 = f (N, Q_, Q_) \ qquad (2) \ end {equação} $$ display $$

e especifique variáveis ​​independentes (x_digit) e dependentes (y_digit).

 x_digit = [N Qm Ql ones(size(N,1),1)]; %  N,   Q,   Q,   y_digit = Q0; %    Q0 

Se você não entender por que a matriz x_digit tem um único vetor (última coluna), leia os materiais de regressão linear. No tópico da análise de regressão, recomendo o livro Draper N., Smith H. Análise de regressão aplicada . Nova York: Wiley, No prelo, 1981. 693 p. (disponível em russo).

Equação da característica de fluxo linearizado de uma turbina a vapor

$$$$ display $$ \ begin {equation} Q_0 = \ alpha_N \ cdot N + \ alpha_T \ cdot Q_P + \ alpha_T \ cdot Q_T + \ alpha_0 \ qquad (3) \ end {equação} $$ display $$

é um modelo de regressão linear múltipla. Os coeficientes α _i serão determinados usando o "grande benefício da civilização" - o método dos mínimos quadrados. Separadamente, observo que o método dos mínimos quadrados foi desenvolvido por Gauss em 1795.

No MATLAB, isso é feito em uma linha.

 A = regress(y_digit, x_digit); fprintf(': a(N) = %4.3f, a(Q) = %4.3f, a(Q) = %4.3f, a0 = %4.3f\n',... A); 

A variável A contém os coeficientes desejados (consulte a mensagem na linha de comando do MATLAB).

Assim, a característica de vazão linearizada obtida da turbina a vapor PT-80 tem a forma

$$$$ display $$ \ begin {equação} Q_0 = 2,317 \ cdot N + 0,621 \ cdot Q_ + 0,255 \ cdot Q_ + 33,874 \ qquad (4) \ end {equação} $$ display $$

4) Estimamos o erro de linearização da característica de fluxo obtida.

 y_model = x_digit * A; err = abs(y_model - y_digit) ./ y_digit; fprintf('  = %1.3f, (%4.2f%%)\n\n', mean(err), mean(err)*100); 

O erro de linearização é de 0,57% (consulte a mensagem na linha de comandos do MATLAB).

Para avaliar a conveniência de usar a característica de fluxo linearizado de uma turbina a vapor, resolvemos o problema de calcular a taxa de fluxo de vapor de alta pressão Q ₀ em valores de carga conhecidos N, Q _p , Q _t .

Seja N = 82,3 MW, Q _p = 55,5 MW, Q _t = 62,4 MW, então

$$$$ display $$ \ begin {equação} Q_0 = 2,317 \ cdot 82,3 + 0,621 \ cdot 55,5 + 0,255 \ cdot 62,4 + 33,874 = 274,9 \ qquad (5) \ end {equação} $$ exibir $$

Deixe-me lembrá-lo de que o erro médio de cálculo é de 0,57%.

Voltemos à questão: por que a característica de fluxo linearizado de uma turbina a vapor é fundamentalmente mais conveniente do que os nomogramas de consumo específico qt bruto para a geração de eletricidade? Para entender a diferença fundamental na prática, resolva dois problemas.

1. Calcule Q ₀ com a precisão indicada usando os nomogramas e seus olhos.
2. Automatize o processo de cálculo de Q ₀ usando nomogramas.

Obviamente, na primeira tarefa, a determinação de q valores brutos pelo olho é repleta de erros grosseiros.

A segunda tarefa é difícil de automatizar. Como os valores q q são grosseiramente não-lineares , para essa automação, o número de pontos digitalizados é dez vezes maior que no exemplo atual. A digitalização sozinha não é suficiente, também é necessário implementar um algoritmo para interpolar (encontrar valores entre pontos) de valores brutos não lineares.

Etapa 3. Determinando os limites da faixa de ajuste da turbina a vapor

1. Cálculos

Para calcular a faixa de ajuste, usaremos outro “bem da civilização” - o método do casco convexo, casco convexo.

No MATLAB, isso é feito da seguinte maneira.

 indexCH = convhull(N, Qm, Ql, 'simplify', true); index = unique(indexCH); regRange = [N(index) Qm(index) Ql(index)]; regRangeQ0 = [regRange ones(size(regRange,1),1)] * A; fprintf('     = %d\n\n', size(index,1)); 

O método convhull () determina os pontos limite da faixa de ajuste fornecidos pelos valores das variáveis ​​N, Qm, Ql. A variável indexCH contém os vértices dos triângulos construídos usando a triangulação de Delaunay. A variável regRange contém os pontos de limite da faixa de ajuste; variável regRangeQ0 - vazões de vapor de alta pressão para os pontos limites da faixa de controle.

O resultado do cálculo pode ser encontrado no arquivo PT_80_linear_characteristic_curve.xlsx, folha “PT-80-result”, tabela “Limites da faixa de ajuste”.

Característica de fluxo linearizada construída. É uma fórmula (4) e 37 pontos que definem os limites (casca) da faixa de ajuste na tabela correspondente.

2. Verificação

Ao automatizar os processos de cálculo, Q ₀ , é necessário verificar se algum ponto com os valores de N, Q _p , Q _{t está} dentro da faixa de ajuste ou fora dela (o modo não é tecnicamente viável). No MATLAB, isso pode ser feito da seguinte maneira.

Definimos os valores de N, Q _p , Q _t que queremos verificar.

 n = 75; qm = 120; ql = 50; 

Nós verificamos.

 in1 = inpolygon(n, qm, regRange(:,1),regRange(:,2)); in2 = inpolygon(qm, ql, regRange(:,2),regRange(:,3)); in = in1 && in2; if in fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f     \n', n, qm, ql); else fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f      ( )\n', n, qm, ql); end 

A verificação é realizada em duas etapas:

• a variável in1 indica se os valores de N, Q _p caíram na projeção da casca no eixo N, Q _p ;
• da mesma forma, a variável in2 mostra se os valores de Qp, Qt _estão dentro da projeção da casca no eixo de Qp, Qt.

Se as duas variáveis ​​forem iguais a 1 (verdadeiro), o ponto desejado estará dentro da carcaça, que define a faixa de ajuste da turbina a vapor.

Ilustração da característica de fluxo linearizado obtido de uma turbina a vapor

Os mais "benefícios generosos da civilização" que obtivemos em termos de ilustração dos resultados dos cálculos.

Primeiro, devemos dizer que o espaço em que construímos os gráficos, ou seja, o espaço com os eixos x - N, y - Qt, z - Q0, w - Qp, é chamado de espaço de regime (consulte Otimização da operação de usinas termelétricas nas condições mercado grossista de electricidade e capacidade da Rússia

) Cada ponto deste espaço define um determinado modo de operação de uma turbina a vapor. O modo pode ser

• tecnicamente viável, se o ponto estiver dentro do casco que define a faixa de ajuste,
• tecnicamente inviável se o ponto estiver fora desse shell.

Se falarmos sobre o modo de operação de condensação de uma turbina a vapor (Q _p = 0, Q _t = 0), a característica de fluxo linearizado é um segmento de linha reta . Se falamos de uma turbina do tipo T, a característica de fluxo linearizado é um polígono plano no espaço de regime tridimensional com os eixos x - N, y - Qt, z - Q0, que é fácil de visualizar. Para uma turbina do tipo PT, a visualização é a mais difícil, pois a característica de fluxo linearizada de uma turbina é um polígono plano no espaço quadridimensional (para explicações e exemplos, consulte Otimizando a operação de usinas termelétricas no mercado atacadista de eletricidade e energia da Rússia, seção Linearização da característica de fluxo da turbina ).

1. Ilustração das características de vazão linearizada obtidas de uma turbina a vapor

Vamos construir os valores da tabela "Dados de entrada (unidade de potência)" no espaço do regime.

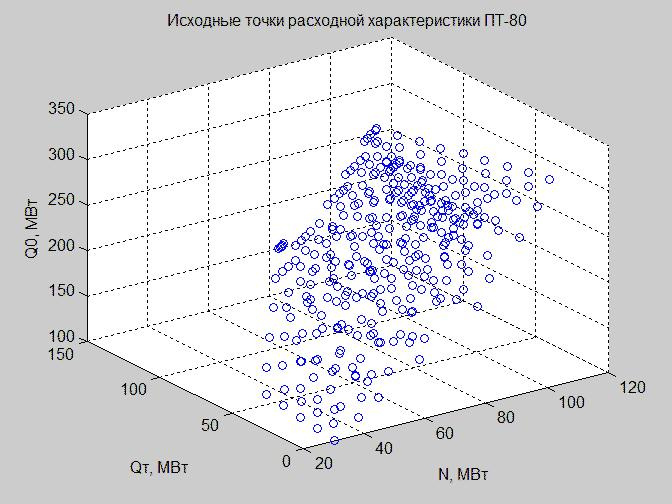
Fig. 3. Os pontos de partida das características de fluxo no espaço de regime com os eixos x - N, y - Q _t , z - Q ₀

Como não podemos construir dependência no espaço quadridimensional, ainda não atingimos esse bem da civilização, operamos com os valores de Q _{n da} seguinte maneira: excluí-los (Fig. 3), corrigir (Fig. 4) (consulte o código para a construção de gráficos no MATLAB).

Fixamos o valor de Q _p = 40 MW e construímos os pontos de partida e a característica de vazão linearizada.

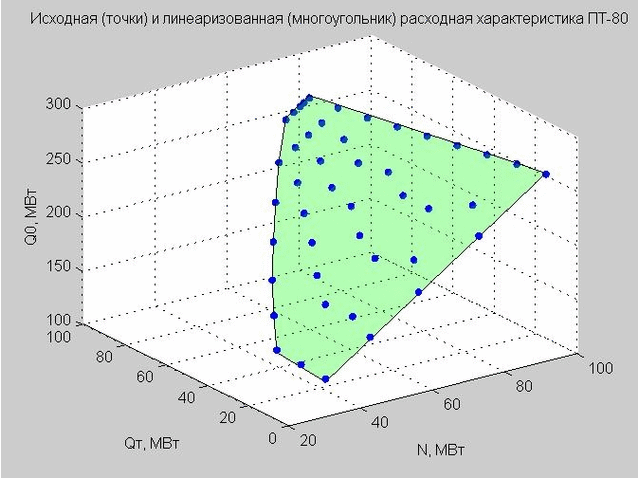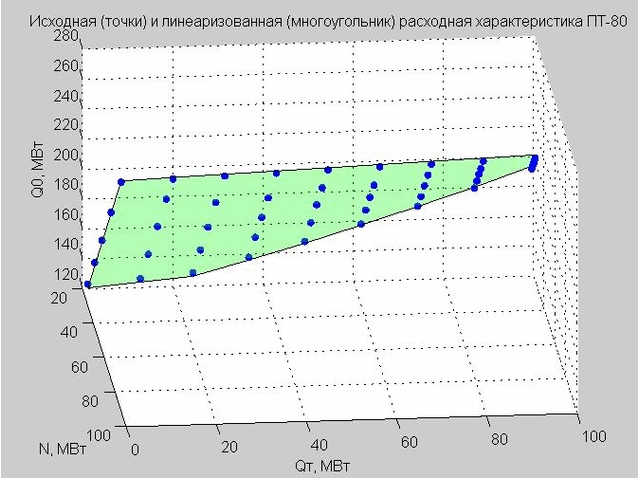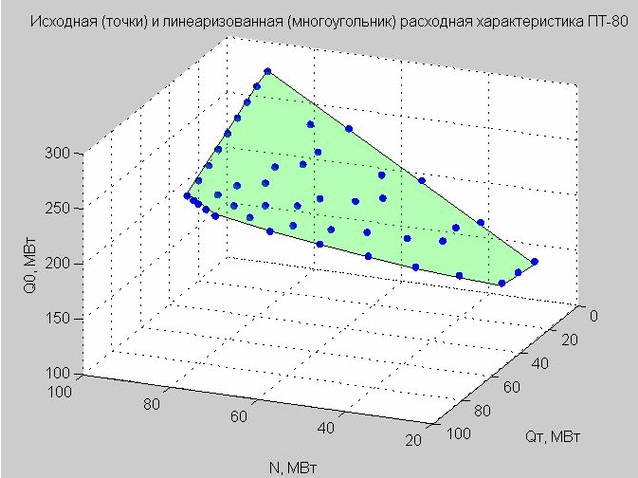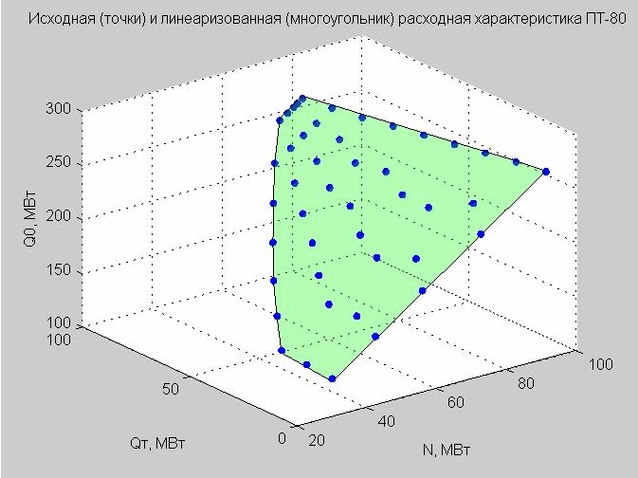
Fig. 4. Pontos de partida da característica de descarga (pontos azuis), característica de descarga linearizada (polígono plano verde)

Voltemos à fórmula da característica de vazão linearizada (4) que obtivemos. Se fixarmos Q _p = 40 MW MW, a fórmula terá a forma

$$$$ display $$ \ begin {equação} Q_0 = 2.317 \ cdot N + 0.255 \ cdot Q_T + 58.714 \ qquad (6) \ end {equação} $$ display $$

Este modelo define um polígono plano no espaço tridimensional com os eixos x - N, y - Qt, z - Q0 por analogia com uma turbina do tipo T (veremos na Fig. 4).

Muitos anos atrás, quando q nomogramas brutos foram desenvolvidos, um erro fundamental foi cometido na etapa de análise dos dados iniciais. Em vez de aplicar o método dos mínimos quadrados e construir uma característica de fluxo linearizado de uma turbina a vapor por um motivo desconhecido, eles fizeram um cálculo primitivo:

$$$$ display $$ \ begin {equação} Q_0 (N) = Q_ = Q_0 - Q_ - Q_ \ qquad (7) \ end {equação} $$ display $$

Subtraída da vazão do vapor de alta pressão Q _{0, a} vazão dos vapores Q _t , Q _p e atribuída a diferença resultante Q ₀ (N) = Q _e à geração de eletricidade. O valor obtido Q ₀ (N) = Q _{e foi} dividido por N e convertido em kcal / kW · h, tendo recebido um consumo específico q _t bruto. Este cálculo não está em conformidade com as leis da termodinâmica.

Caros leitores, talvez você saiba o motivo desconhecido? Compartilhe!

2. Ilustração da faixa de ajuste da turbina a vapor

Vamos ver a concha da faixa de ajuste no espaço do regime. Os pontos de partida para sua construção são apresentados na Fig. 5. Estes são os mesmos pontos que vemos na fig. 3, no entanto, o parâmetro Q ₀ agora _está excluído.

Fig. 5. Os pontos de partida das características de fluxo no espaço de regime com os eixos x - N, y - Q _p , z - Q _t

Muitos pontos na fig. 5 é convexo. Usando a função convexhull (), definimos os pontos que definem a casca externa desse conjunto.

A triangulação de Delaunay (um conjunto de triângulos conectados) nos permite construir a concha da faixa de ajuste. Os vértices dos triângulos são os valores limites da faixa de ajuste da turbina a vapor PT-80 em consideração.

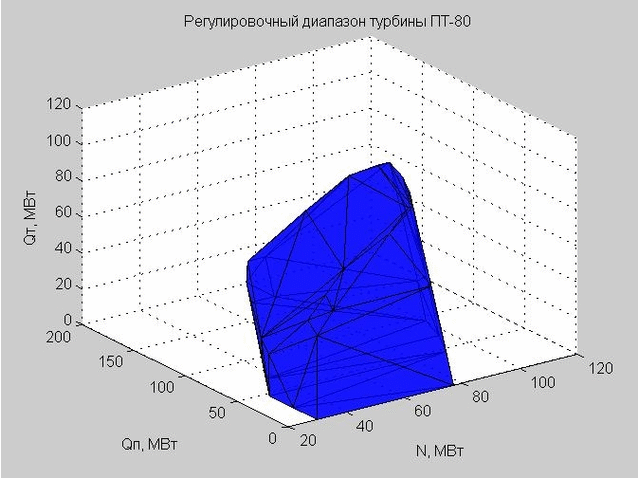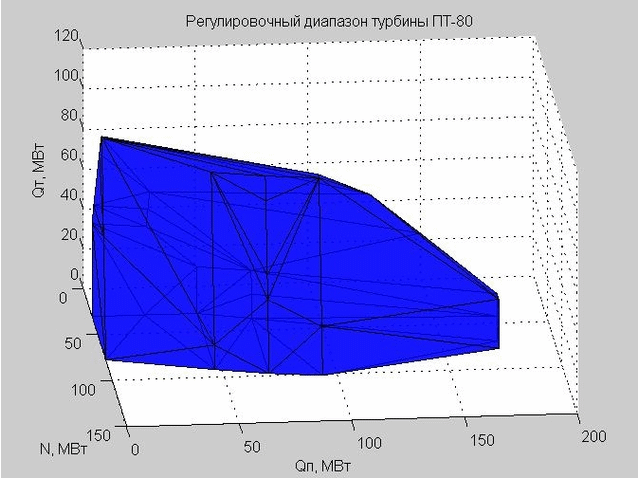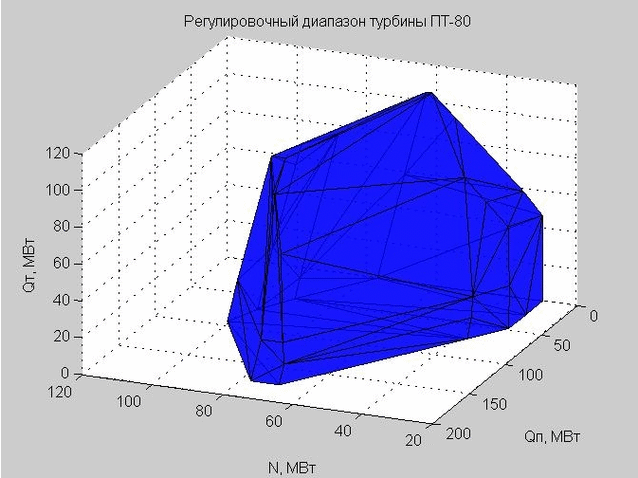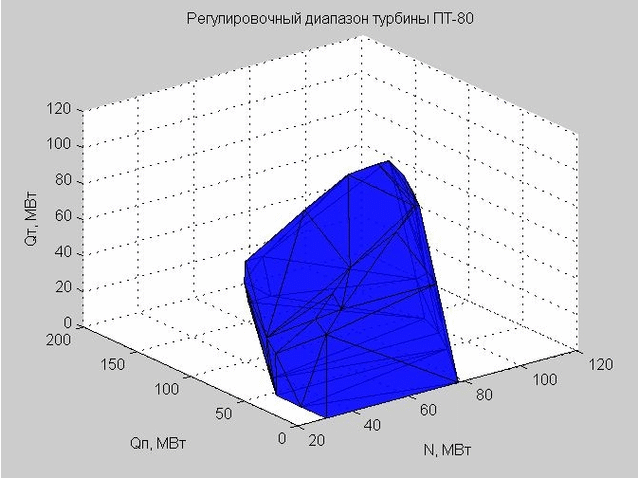
Fig. 6. A concha da faixa de ajuste, representada por muitos triângulos

Quando fizemos uma verificação em um determinado ponto para entrar na faixa de ajuste, verificamos se esse ponto está dentro ou fora do shell resultante.

Todos os gráficos apresentados acima são construídos usando as ferramentas MATLAB (consulte PT_80_linear_characteristic_curve.m).

Tarefas promissoras relacionadas à análise da operação de uma turbina a vapor usando uma característica de fluxo linearizado

Se você está fazendo um diploma ou dissertação, posso oferecer várias tarefas, cuja novidade científica você pode facilmente provar para o mundo inteiro. Além disso, você fará um trabalho excelente e útil.

Tarefa 1

Mostre como o polígono plano muda quando a pressão de vapor de baixa pressão Qt muda.

Tarefa 2

Mostre como o polígono plano muda quando a pressão no condensador muda.

Tarefa 3

Verifique se os coeficientes da característica de fluxo linearizado podem ser representados como funções de parâmetros adicionais do regime, a saber:

$$$$ display $$ \ begin {equação} \ alpha_N = f (p_ {0}, ...); \\ \ alpha_P = f (p_ {P}, ...); \\ \ alpha_T = f (p_ {T}, ...); \\ \ alpha_0 = f (p_ {2}, ...). \ end {equação} $$ display $$

Aqui p ₀ é a pressão de vapor de alta pressão, p _p é a pressão de vapor de média pressão, p _t é a pressão de vapor de baixa pressão, p ₂ é a pressão de vapor de exaustão no condensador, todas as unidades são kgf / cm2.

Justifique o resultado.

Referências

Chuchueva I.A., Inkina N.E. Otimização do CHP nas condições do mercado atacadista de energia elétrica e capacidade da Rússia // Ciência e Educação: Edição Científica do MSTU. N.E. Bauman. 2015. No. 8. S. 195-238.

• Seção 1. Declaração substantiva do problema de otimizar o funcionamento do CHP na Rússia
  
• Seção 2. Linearização da característica de fluxo da turbina
  
• Seção 3. Declaração formal do problema de otimização de curto prazo da operação de CHPPs em um setor de mercado de energia elétrica
  
• Seção 4. Experiência computacional
  
• Referências com comentários
  
• Comparação das tarefas de otimização 1 e 2 na determinação da composição ideal do equipamento incluído

Chuchueva I.A. Métodos computacionais para determinar o consumo específico de combustível equivalente de usinas termelétricas para energia elétrica e térmica fornecida no modo de geração combinada // Science and Education: Publicação científica do MSTU. N.E. Bauman. 2016. No. 2. P. 135-165.

• Seção 1. Declaração do problema
  
• Seção 2. Visão Geral do Método
  
• Seção 3. Um novo método para calcular o consumo específico de combustível equivalente
  
• Seção 4. Comparação de Métodos
  
• Referências
  

Característica de fluxo linearizado de uma turbina a vapor.

• Parte 1. Questões-chave
  
• Parte 2. Exemplo de construção da turbina PT-80 no MATLAB
  
• Parte 3. Dissipando mitos sobre modos de operação de turbinas a vapor