Massa, energia, momento e a lei da conservação

Muitas propriedades obscuras do mundo estão associadas à natureza da massa e energia (além do momento). Todos nós ouvimos essas palavras e muitos de nós têm uma vaga idéia de seu significado. Obviamente, os significados das palavras "massa" e "energia" em inglês e em outros idiomas são muitos. Infelizmente, nenhum deles coincide com o que os físicos têm em mente. Tente deixar de lado esses significados das palavras e trabalhe com conceitos físicos exatos - caso contrário, você ficará completamente confuso.

Note-se que não se deve recordar outro par popular, "substância e energia", com a frase "massa e energia". Muitas pessoas mencionam a última frase como se matéria e energia fossem dois lados da mesma moeda. Mas isso não é verdade. Matéria e energia se enquadram em diferentes categorias, como maçãs e orangotangos. Uma substância, não importa como defini-la, é uma classe de objetos existentes no Universo, e massa e energia não são objetos, mas as propriedades que esses objetos possuem. Massa e energia estão profundamente interligadas entre si e merecem uma explicação geral.

Para entender massa e energia, você precisa adicionar impulso a elas e discutir as diferenças e os relacionamentos dessas quantidades.

Energia

A palavra "energia" tem muitos significados. Quando adoecemos, dizemos que não temos mais energia, referindo-nos à força e motivação. Quando dizemos que alguém está cheio de energia, queremos dizer sua alta atividade. Nós reclamamos sobre o aumento dos preços da energia, referente ao combustível. Estamos falando de energia espiritual como algo incomensurável, mas importante, talvez alguma forma de carisma. E todos esses conceitos se sobrepõem, então escolhemos uma palavra para descrevê-los. Mas na física, a energia é uma coisa completamente diferente. Do ponto de vista da física, uma dessas definições será confundida erroneamente com a física. Na física, é preciso aderir a um termo físico para não obter as respostas erradas e não ficar completamente confuso.

Infelizmente, o conceito de "energia" na física é muito difícil de descrever como os dicionários - com uma frase curta e significativa. Mas não pense mal - a coisa toda é a imperfeição da linguagem natural, e não que o conceito de energia na física seja vago. Em qualquer sistema físico, é completamente claro qual é a sua energia, tanto no sentido de sua medição experimental quanto no de cálculos (se houver equações descrevendo o sistema).

Uma das razões pelas quais a energia é tão difícil de descrever é que ela pode assumir várias formas, e nem todas são fáceis de entender. Aqui estão três variedades comuns:

1. A energia pode ser encerrada na massa de um objeto. Aqui eu chamo essa opção de "energia de massa" (graças à conhecida equação E = mc ^{2, a} energia se liga à massa. Também é chamada de "energia de repouso", pois é a energia de um objeto em repouso, ou seja, sem movimento).

2. Em segundo lugar, a energia está associada ao movimento de um objeto. Aqui eu chamo de "energia de movimento", e o termo técnico para isso é energia cinética. Essa opção é intuitivamente fácil de entender, porque objetos em movimento rápido têm mais energia que objetos em movimento lento. Além disso, um objeto pesado possui mais energia de movimento do que um objeto leve que se move na mesma velocidade.

3. A energia pode ser armazenada no relacionamento dos objetos (e geralmente é chamado de "potencial"). Ele é armazenado em uma fonte esticada, na água atrás da barragem, na interação gravitacional da Terra e do Sol, nas interações dos átomos da molécula. Existem muitas maneiras de armazenar energia. Parece vago, mas o idioma é o culpado. Em qualquer um desses casos, existem fórmulas exatas que descrevem a energia armazenada no sistema e maneiras bem definidas de medi-la.

O terceiro tipo de energia está conectado com o que chamarei de energia de interação, e este é o conceito mais confuso de todos. Ao contrário da energia da massa e da energia do movimento, que são sempre maiores ou iguais a zero, a energia das interações pode ser positiva e negativa. Até agora, deixarei este tópico, mas retornaremos a ele.

A energia é uma quantidade especial de grande importância para a física. A razão para essa importância é que ela é "preservada". O que isso significa?

Se você iniciar a observação com um objeto ou com um conjunto de objetos - nós os chamaremos de "sistema de objetos" - possuindo uma certa quantidade de energia no momento inicial (não se esqueça de calcular toda a energia - massas, movimentos, energia armazenada de todos os tipos, etc.) e depois partes do sistema irão interagir apenas entre si e com mais nada; então, no final da observação, a quantidade total de energia possuída por esses objetos será a mesma do início. A energia total do sistema é conservada - sua quantidade total não muda. Pode mudar de forma, mas se você acompanhar todas as variedades, no final será o mesmo que no começo.

Essa regra funciona mesmo que alguns objetos desapareçam e dêem lugar a outros, por exemplo, se uma partícula no sistema se decompor em duas outras se fundirem no sistema.

Por que a energia é economizada? Por causa do princípio matemático, correlacionar o fato de que as leis da natureza não mudam ao longo do tempo, com a existência de uma quantidade conservada, que por definição chamamos de "energia".

Devemos a definição mais famosa e geral desse princípio a Emmy Noether , um dos maiores físicos matemáticos do século anterior, contemporâneo de Einstein. Alguns membros da comunidade física e matemática a trataram com profundo respeito , mas naquela época na Alemanha natal, ela sofria de discriminação com base no gênero e na nacionalidade (lá eles bloquearam tentativas de atribuir a ela o título de professora em Göttingen , e dali ela teve que fugir depois os nazistas chegaram ao poder). Depois de emigrar para os Estados Unidos, após apenas dois anos de ensino no Brin-Mar College (que até hoje só aceita mulheres para treinamento), ela morreu de câncer.

O famoso teorema de Noether (na verdade esses são dois teoremas intimamente relacionados) nos diz que, se houver simetria nas leis da natureza - no nosso caso, isso significa que as leis da natureza são as mesmas a qualquer momento -, isso preserva uma certa quantidade - no nosso caso, energia .

Além disso, o teorema nos diz exatamente qual é a magnitude - quais são as diferentes formas de energia para um determinado sistema de objetos que precisam ser adicionados para obter energia total. É por isso que os físicos sempre sabem exatamente o que é energia e por que é mais fácil obter usando equações do que definir em palavras.

Impulso

A situação com momento é aproximadamente a mesma que com energia. As leis da natureza são as mesmas em todo lugar. A grosso modo, os experimentos dão as mesmas respostas, se você os gasta ao norte ou sul daqui, oeste ou leste, no topo de um edifício ou em um poço profundo. Escolha qualquer direção no espaço. Então, de acordo com Noether, o momento nessa direção é conservado. Como existem três dimensões no espaço, é possível mover-se em três direções independentes diferentes e existem três leis de conservação independentes. Você pode escolher quaisquer três direções, desde que sejam diferentes. Por exemplo, você pode escolher pulsos nas direções norte-sul, oeste-leste e cima-baixo como as três leis de conservação. Ou você pode escolher três outros - na direção de e para o Sol, ao longo da órbita da Terra em ambas as direções, e para cima e para baixo em relação ao plano do sistema solar. Sua escolha não importa, porque o momento é armazenado em qualquer direção.

A forma mais simples de impulso surge devido ao simples movimento de objetos, e isso é algo que pode ser imaginado intuitivamente: se um objeto se move em uma certa direção, então ele tem um impulso nessa direção e, quanto mais rápido ele se move, maior é esse impulso. E um objeto mais pesado tem um momento maior que um leve se se mover na mesma velocidade.

Uma das conseqüências interessantes dessa conservação: se você tem um sistema imóvel de objetos (ou seja, o sistema como um todo não se move, se você calcula a média de todos os movimentos de seus objetos constituintes), ele permanecerá imóvel, a menos que seja dado algum movimento externo impacto. A razão é que, em um sistema fixo, o momento total é zero e, como o momento é preservado, permanecerá zero para sempre, a menos que intervenha de fora do sistema.

Massa e sua relação com energia e momento

Agora vamos voltar à massa

Infelizmente, muita confusão está associada à massa - após a publicação do trabalho de Einstein sobre a teoria da relatividade por algum tempo, havia dois conceitos de massa. E apenas um deles (aquele em que o próprio Einstein parou, e que às vezes é chamado de "massa invariável" ou "massa em repouso" para distingui-lo do termo já arcaico "massa relativista"), ainda é usado na física de partículas. Em um artigo separado, explicarei isso com mais detalhes.


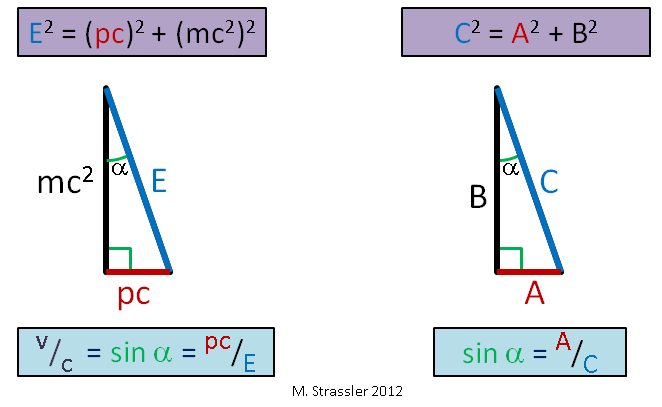Fig. 1

Por massa m, que uso nos artigos, entende-se a massa que liga diretamente energia e momento. Para um objeto que se move sem a influência de forças externas (não interagindo significativamente com outros objetos), Einstein sugeriu (e isso foi confirmado por experimentos) que sua energia E, momento p e massa m satisfazem a simples igualdade pitagórica:

$$

$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2 \ qquad (equação No. 1)$$

Lembre-se dos antigos Pitágoras que afirmavam que, para um triângulo retângulo com os lados A e B e hipotenusa C, a igualdade $$$C ^ 2 = A ^ 2 + B ^ 2$ ? Esta é uma conexão do mesmo tipo - veja a fig. 1. Conosco, c é uma velocidade constante, que, como veremos, serve como limite de velocidade universal. Também veremos por que isso é chamado de "velocidade da luz".

De acordo com as equações de Einstein, a velocidade de um objeto dividido pelo limite de velocidade c é apenas a razão de pc para E:

$$

$$v / c = (p c) / E \ qquad (equação # 2)$$

Ou seja, a proporção da perna horizontal para a hipotenusa. Também é igual ao seno do ângulo α na Fig. 1. Então aqui, cidadãos. E como as pernas de um triângulo retângulo são sempre menores que a hipotenusa (o seno de qualquer ângulo é sempre menor ou igual a 1), a velocidade de qualquer objeto não pode exceder s, o limite universal de velocidade. Com o aumento da velocidade de um objeto de massa fixa, p e E se tornam muito grandes (Fig. 2), mas E é sempre maior que pc, portanto v é sempre menor que c!


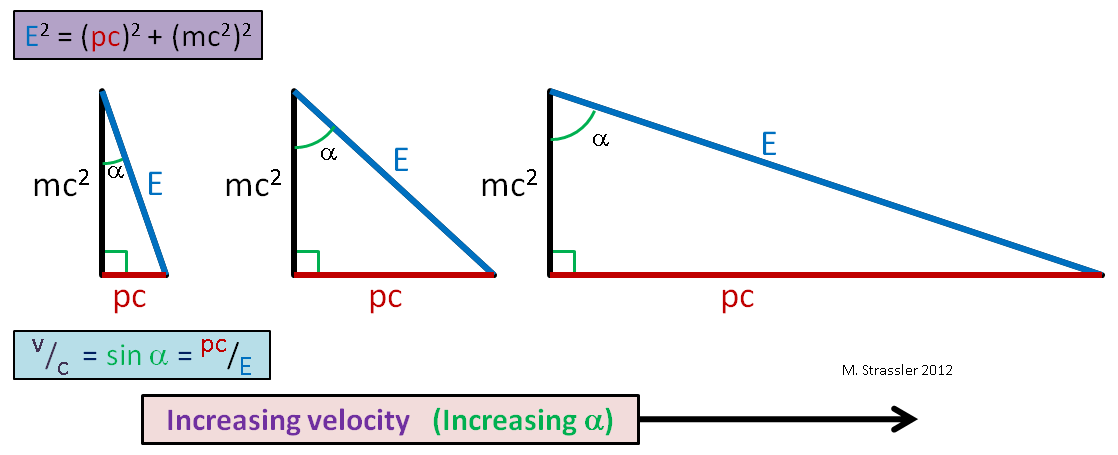Fig. 2

Agora observe que, se o objeto não se mover, seu momento p será igual a zero e a razão na equação 1 reduzirá para:

$$

$$E ^ 2 = (mc ^ 2) ^ 2, \ quad ou \ quad E = mc ^ 2$$

A famosa fórmula de Einstein, a relação de massa com uma quantidade fixa de energia (o que eu chamo de energia de massa), é simplesmente uma afirmação correspondente ao fato de que quando um triângulo se degenera em uma linha vertical, como na Fig. 3 à esquerda, sua hipotenusa se torna do mesmo comprimento da perna vertical. Ao mesmo tempo, isso não significa que a energia seja sempre igual à massa vezes o quadrado s. Isso funciona apenas para um objeto em repouso com momento zero.


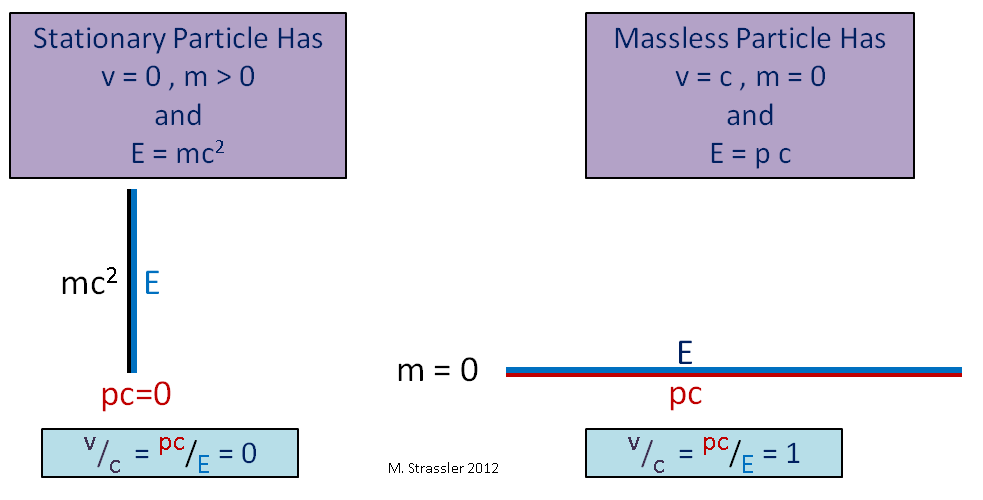Fig. 3

Outra observação interessante: para uma partícula sem massa, a perna vertical do triângulo é zero e a hipotenusa e a perna horizontal são as mesmas, como na Fig. 3. Nesse caso, E é pc, o que significa que v / c = 1 ou v = c. É visto que uma partícula sem massa (por exemplo, um fóton, uma partícula de luz) se move inevitavelmente a uma velocidade de c. Portanto, a velocidade da luz é igual ao limite de velocidade universal, s.

Por outro lado, se pegarmos uma partícula com massa, como na Fig. 4, não importa o tamanho do momento e da energia, E sempre será um pouco mais do que p * c; portanto, a velocidade sempre será menor que s. Partículas sem massa devem viajar na velocidade máxima. A velocidade de partículas maciças deve ser menor.


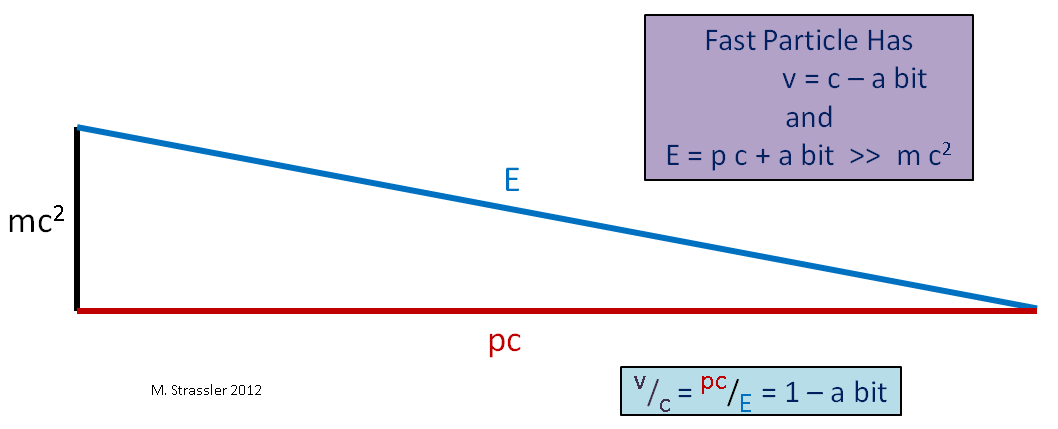Fig. 4. Aqui ">>" significa "muito mais"

Imagine outro caso limítrofe, um objeto maciço que se move lentamente (em comparação com a velocidade da luz), como um carro. Como sua velocidade v é muito menor que c, seu momento p vezes c será muito menor que E e, como pode ser visto na Fig. 5, E será um pouco mais do que mc ² . Portanto, a energia do movimento de um objeto lento E - mc ^{2 é} muito menor que a energia de sua massa mc ² , e para um objeto rápido a energia do movimento pode ser arbitrariamente grande, como vimos na Fig. 4)

Um ponto sutil: o momento não é apenas um número, mas também um vetor. Ele tem magnitude e direção. É direcionado para o movimento da partícula. Quando escrevo p, apenas indico o valor. Em muitos casos, é necessário rastrear a direção do pulso, embora na equação nº 1, que relaciona o pulso à energia e massa, isso não seja necessário.


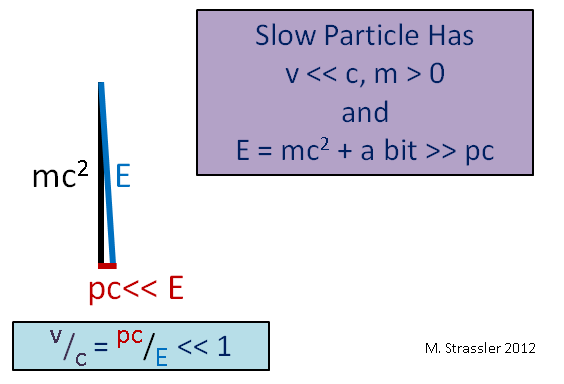Fig. 5

Outro ponto sutil: usei triângulos e trigonometria simples, pois é conhecida por todos da escola. Os especialistas precisam ter mais cuidado - você pode entender corretamente as equações de Einstein usando funções hiperbólicas que geralmente não são encontradas por amadores, mas são extremamente importantes para entender a estrutura da teoria e tornar as coisas mais compreensíveis, como adição de velocidade, compressão de distância etc. Pessoas que não pretendem ser especialistas podem ignorar isso.

Mas a velocidade é relativa?

Se você ler atentamente o texto, algo já poderá surpreendê-lo. Você sabe que a velocidade de uma partícula - ou qualquer coisa que se mova mais lentamente que a luz - depende do ponto de vista.

Se você se sentar em casa e ler um livro, dirá que a velocidade do livro é zero (e realmente descansa em relação a você); portanto, ele não possui impulso e energia de movimento, apenas energia de massa. Mas se eu estivesse na lua, lembraria que a Terra está girando, de modo que essa rotação o cativa e o move em relação a mim a uma velocidade de centenas de quilômetros por hora. Então você e seu livro teriam o impulso do meu ponto de vista.

Quem está certo?

A variante da relatividade de acordo com Galileu - o primeiro princípio da relatividade - afirma que ambos estamos certos. A variante de relatividade de Einstein concorda com o ponto de vista de Galileu de que ambos estão certos, mas faz ajustes importantes em como os seguidores de Galileu indicariam a energia, momento e massa do livro, colocando essas quantidades na relação pitagórica da equação no. 1.

Mas se tudo estiver certo, qual E e qual p devo substituir na proporção de energia / momento / massa, $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ ? Substitua E ep medido por você lendo o livro, ou seja, E = mc ² ep = 0? Ou substitua E e p, que o livro tem do meu ponto de vista, quando você se move com a Terra?

A resposta a esta pergunta contém toda a essência da equação de Einstein Nº 1. Cada observador medirá diferentes valores de E ep para o livro, dependendo da velocidade com que o livro se moverá em relação a ele. Mas para todos os observadores a equação $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ será verdade!

A magia! Mas, de fato, gênio é uma idéia que surgiu em 1905 sobre como substituir o conjunto de equações proposto por Newton e seus seguidores por um novo conjunto surpreendente de equações, que ainda coincide com todos os experimentos anteriores, mas acabou sendo uma representação mais precisa da realidade. É difícil imaginar o quanto foi necessário mudar a maneira de pensar para pensar até que você descubra quanto tudo poderia dar errado durante a formação da nova teoria e quantas outras equações diferentes contêm contradições com a matemática ou com experimentos anteriores. Seria oferecer (e as pessoas os ofereceram). Por exemplo, o trabalho de físicos novatos vem constantemente a mim, tentando "consertar" as equações de Einstein, mas nunca vi nenhum deles verificar suas equações quanto à consistência interna. Essa é uma tarefa muito difícil e a razão do fracasso da maioria das teorias.

Mas como então a energia e o momento podem ser conservados?

Espere um minuto, você diz, quando sua cabeça estiver pronta para explodir e respingar tudo ao seu redor com seu cérebro (eu me lembro dessa sensação), mas a energia e o momento devem ser preservados! Então, como diferentes observadores podem discordar do que são?

Há ainda mais magia, que, aliás, estava antes de Einstein. Acredite, o Universo é um contador muito, muito inteligente e, apesar de diferentes observadores não concordarem com a energia disponível em um objeto ou sistema de objetos, todos concordam que essa energia não muda com o tempo. O mesmo vale para o momento.

Mas a massa é muito diferente da energia e do momento. Primeiro, a massa não é conservada. Na natureza, existem muitos processos que alteram a massa total de um sistema: por exemplo, uma partícula massiva de Higgs pode decair em dois fótons sem massa. Nenhuma simetria está associada à massa e, portanto, Noether não tem lei de conservação para nós. Em segundo lugar, diferentemente da energia e do momento, cujos valores dependem do observador (em particular, de sua velocidade em relação aos objetos medidos), todos os observadores concordam com a massa m do objeto. E isso não é de todo óbvio, e acontece porque as equações de Einstein funcionam terrivelmente astuciosamente.

Então, o que nós temos

No momento, temos vários conhecimentos, à primeira vista, conflitantes. Sabemos que:

• A energia e o momento de um sistema físico isolado são conservados (a energia total e o momento total de um sistema isolado não mudam com o tempo) do ponto de vista de qualquer observador.
• Observadores diferentes, movendo-se um em relação ao outro, avaliarão os valores da energia e do momento do sistema de maneira diferente!
• A soma das massas dos objetos que compõem o sistema não é salva, pode mudar.
• Mas todos os observadores concordam com a massa do objeto.

Mais dois fatos e duas conclusões devem ser adicionados a esta lista:

A massa do sistema físico de objetos não é igual à soma das massas dos objetos que compõem esse sistema.

Em vez disso, a massa do sistema físico, com a qual todos os observadores concordam, é determinada por sua energia e momento e satisfaz sua versão da equação nº 1:

$$

$$(E_{system})^2 = (p_{system} c)^2 + (m_{system} c^2)^2 \qquad ( №1')$$

Acontece que não é necessária uma lei de conservação adicional e que, embora a soma das massas dos objetos que compõem o sistema não seja preservada, a massa do sistema é preservada, pois está conectada pela equação 1 'à energia e momento do sistema que são armazenados.

A massa do sistema de objetos é o único item da nossa lista que é simultaneamente preservado e não sujeito a debate pelos observadores.

Você só precisa lembrar que a massa do sistema de objetos não é a soma das massas dos objetos que compõem o sistema, mas o que é dado pela equação nº 1 '.

Do que tentar explicar, basta ver como funciona. Um exemplo vívido vale mais que mil palavras. Vamos considerar como exemplo de um sistema a coisa mais elegante, a saber, uma partícula de Higgs (com uma massa de 126 GeV / s ² ) e veja como as várias declarações feitas acima funcionam quando se decompõem em dois fótons.

Uma partícula de Higgs, dois fótons e três observadores

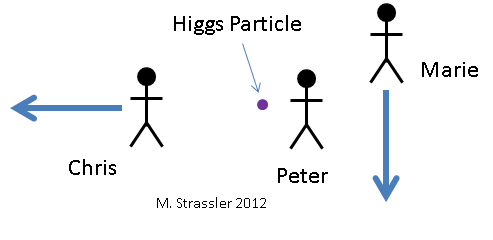Fig. 6. Três observadores olham para a partícula de Higgs. Em relação a ela, Petya (Peter) não se move, Masha (Marie) se move para baixo e Kostya (Chris) se move para a esquerda.

Vejamos como a partícula de Higgs se decompõe em dois fótons, do ponto de vista de três observadores diferentes. Eles são mostrados na fig. 6 junto com a partícula de Higgs que eles estão olhando. Claro, eles não podem vê-la através dos olhos, pois ela existe muito pouco tempo e é muito pequena. Eles precisam usar algum tipo de equipamento científico. Para Petit, a partícula de Higgs não se move. Masha se move para baixo em relação a Petit. Kostya se move para a esquerda em relação a Petit. Assim, para Masha, a partícula de Higgs se move para cima e para Bone - para a direita. Três observadores vêem como uma partícula decai de acordo com a fig. 7. Petya vê que Higgs se decompõe em dois fótons da mesma energia, um dos quais se move para cima e o outro para baixo. Masha vê que Higgs se decompõe em dois fótons de energias diferentes e que uma energia em movimento ascendente tem mais energia do que uma energia em movimento descendente.Kostya vê Higgs decair em dois fótons subindo e descendo. Vamos calcular quais energias e momentos são atribuídos aos Higgs e dois fótons pelos observadores, e como cada um deles chegará à conclusão de que energia e momento são conservados durante a decadência.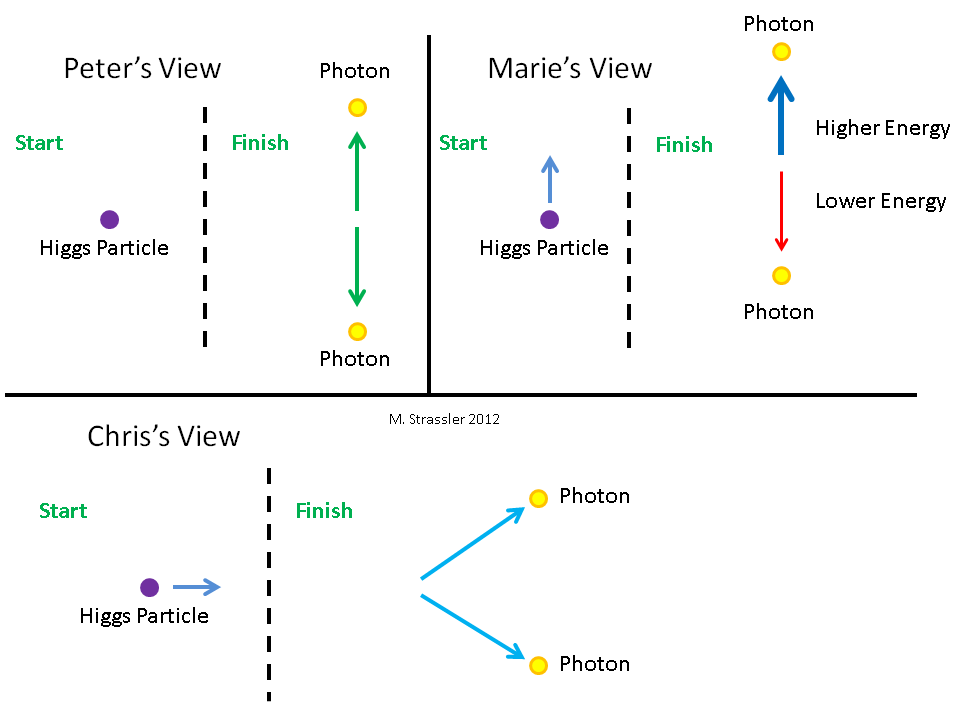

Decaimento de partículas de Higgs

Primeiro, analisamos a partícula de Higgs do ponto de vista de Petit. Petya está olhando (usando instrumentos de medição) a partícula de Higgs, e o que ele vê? (Vou colocar um traço sobre tudo o que Petya vê e depois comparamos isso com as observações de Masha e Kostya). Higgs não se move, então seu impulso$$$\overline{p_0}$é igual a zero e, de acordo com a equação 1, ele, com sua massa m = 126 GeV / c ^{2, a} energia será$$$\overline{E_0} = m c^2 = 126$

Agora, de acordo com a conservação de energia e momento, um sistema que consiste em uma partícula de Higgs conservará toda a energia e momento após a decomposição. E será assim até que nenhuma força externa afete Higgs. Você pode perguntar se precisamos nos preocupar com a gravidade, porque a gravidade será uma influência externa que pode mudar o momento. Minha resposta é que, no curto espaço de tempo em que Higgs se deteriorar, o efeito da gravidade será tão pequeno que, se eu dissesse o quão pequena é realmente, você riria. Esqueça.

Assim, quando Higgs decai, as energias das partículas que compõem seus resíduos devem totalizar 126 GeV, e o momento das partículas (dado que o momento não é apenas uma quantidade, mas também uma direção - um vetor) totalizará zero.

Dois fótons sem massa, nos quais os decaimentos de Higgs podem se espalhar em qualquer direção, mas para simplificar o exemplo, imagine que eles se espalhem verticalmente - um para cima e outro, ricocheteando, para baixo. (Um pouco mais tarde, discutiremos por que eles devem voar em direções opostas).

Que momento têm os fótons? É simples Em primeiro lugar, o momento total do sistema - a soma do momento de dois fótons - deve ser zero, pois Higgs tinha zero momento antes da decadência (do ponto de vista de Petit). Agora, cada um dos fótons tem um impulso de uma certa magnitude e direção. No total, eles podem dar zero de apenas uma maneira - se forem de magnitude igual e na direção oposta. Se um sobe, o outro deve cair e seu tamanho deve ser o mesmo.


Fig. 8: o que Petya vê

Em segundo lugar, a energia total do sistema é a soma das energias de dois fótons. Isso ocorre porque não há energia de interação entre eles (exceto por uma atração gravitacional extremamente pequena, da qual você pode esquecer). Obviamente, como eles não têm massas, toda a sua energia está na energia do movimento. Além disso, no caso de uma partícula sem massa, a equação nº 1 sugere que E = pc, onde p é o momento. Por esse motivo, dois fótons com o mesmo momento devem ter a mesma energia. E como essas duas energias devem somar a energia da partícula de Higgs, a energia de cada fóton deve ser igual a metade da energia da partícula de Higgs.

$$

$$\overline E_1 = \overline E_2 = 1/2 (126 ) = 63$$

E já que para uma partícula sem massa p = E / c, então

$$

$$\overline p_1 = 63 /c \uparrow \\ \overline p_2 = 63 /c \downarrow$$

E é exibido na fig. 8. A

energia e o momento são conservados, mas a massa não, porque os fótons não têm massa, e Higgs o fez. E a massa do sistema? Qual é a massa de um sistema de dois fótons? Diferente de zero. Obviamente o que ela é. Da mesma forma que para o próprio Higgs (do qual todo o sistema foi originalmente composto), um sistema de dois fótons tem a mesma energia e momento que Higgs:

$$

$$E_{system} = \overline E_1 + \overline E_2 = 63 + 63 = 126 \\ p_{system} = \overline p_1 \uparrow + \overline p_2 \downarrow = 63 /c \uparrow + 63 /c \downarrow = 0$$

E desde Petit $$$p_{system} = 0$ ,

$$

$$m_{system} = E_{system} / c^2 = 126 /c^2$$

Essa é a massa de Higgs. A massa do sistema não mudou durante o decaimento, como esperado.

O observador para quem Higgs se move

Masha desce em relação a Peta, então, do seu ponto de vista, Petya e Higgs sobem. Suponha que Higgs se mova a uma velocidade de v = 0,8 s, ou seja, 4/5 da velocidade da luz em relação a ela. Ao contrário de Petya, do ponto de vista de Masha, Higgs tem um momento diferente de zero, e o momento dos fótons se mostra diferente em magnitude, mas ainda multidirecional - como resultado, a soma do momento deles será diferente de zero.


Fig. 9: como Masha vê o decaimento da partícula de Higgs

Como calcular o momento e a energia que Higgs e os dois fótons nos quais ele decai, do ponto de vista de Masha? Para fazer isso, precisamos de outro conjunto de equações simples de Einstein. Suponha que, do ponto de vista de um certo observador, o objeto tenha impulso p e energia E. Então, do ponto de vista de outro observador se movendo com velocidade v na direção do objeto (ou contra ele), o momento e a energia do objeto serão expressos da seguinte forma:

$$

$$p = γ (\overline p+ v \overline E/c^2) \qquad ( №3) \\ E = γ (\overline E + v \overline p) \qquad ( №4)$$

Onde γ satisfaz outra equação pitagórica:

$$

$$1 = v^2/c^2 + 1/γ^2 \qquad ( №5)$$

de acordo com Einstein. Isso nos permite realizar transformações entre o que Petya vê e o que Masha vê (ou qualquer outro observador se movendo com a velocidade v). O que encontramos é mostrado na Fig. 9.

Para comparar as observações de Masha com as de Petya, precisamos v e γ. Argumento que se v = 4/5 c, então γ = 5/3.

Vamos verificar usando a equação nº 5: 1 = (4/5) 2 + (3/5) 2 = 16/25 + 9/25 = 25/25

Petya diz que em Higgs$$$p_0=0, E_0=126$ .E a Masha? Ela diz que:

$$

$$p_0 = γ v \overline E_0 = (5/3) (4/5) \overline E_0 = 168 /c \uparrow \\ E_0 = γ \overline E_0 = (5/3) \overline E_0 = 210$$

Petya afirma que dois fótons $$$\overline E_1 = \overline E_2 = 63$, e para cada um deles E = p c. Agora podemos calcular o que Masha vê usando as equações 4 e 4.

$$

$$E_1= γ (1+v) \overline E_1 = 189 , p_1 = E_1/c \uparrow$$

$$

$$E_2= γ (1-v) \overline E_2= 21 , p_2 =E_2/c \downarrow$$

Isso funciona! A energia também é conservada do ponto de vista de Maria, por

$$

$$E_0 = 210 \\ E_1 + E_2 = (189 + 21) = 210$$

O impulso também é salvo:

$$

$$p_0 = 168 /c \uparrow \\ p_1 + p_2 = 189 /c \uparrow + 21 /c \downarrow = (189 – 21) /c \uparrow = 168 /c \uparrow$$

A massa do sistema coincide com a massa de Higgs antes e depois da decadência, uma vez que antes e depois da decadência

$$

$$E_system = 210 \\ p_system = 168 /c \uparrow$$

Que, de acordo com a equação nº 1 ', traz a massa do sistema de volta para $$$126 /c^2$ como no Petit, porque

$$

$$210^2 = 168^2 + 126^2$$

O observador, do ponto de vista de que Higgs se move para a direita

O que temos com o Bones? Kostya se move para a esquerda em relação a Petya, por exemplo, a uma velocidade de v = 4/5 s, de modo que Higgs (e Petya) se movem para a direita em relação a Kostya a uma velocidade de v = 4/5 s. Os mesmos cálculos que fizemos para Masha mostram que a energia de Higgs$$$E_0 = 210 GeV ep_0 = 168 GeV$ mas, ao contrário de Masha, para quem Higgs se move para cima, para Kostya, o impulso de Higgs é direcionado para a direita. Isso é mostrado na fig. 10)


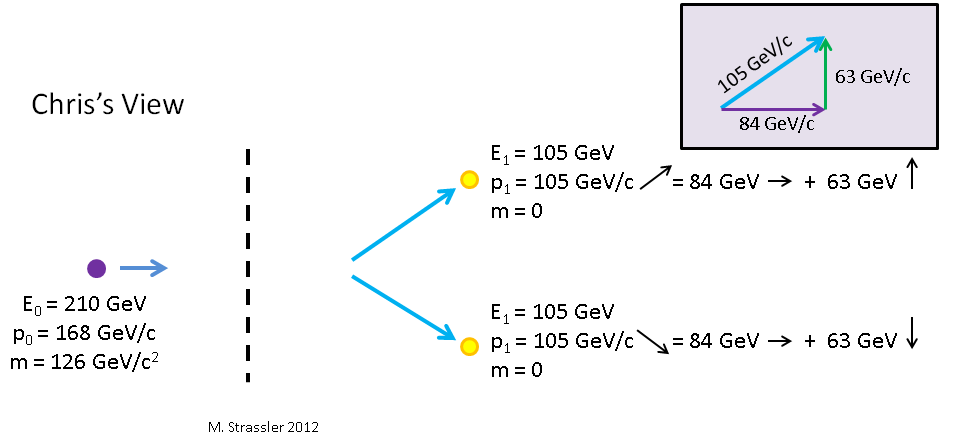
Fig. 10

Higgs decai em dois fótons. Se, do ponto de vista de Petya, os fótons se movem para cima e para baixo, para Kostya, que observa Higgs e Petya se moverem para a direita, um dos fótons se move para a direita e o outro se move para a direita. Que impulso e energia eles terão então?

Através das equações n ° 4 e n ° 5, não sabemos disso, porque são destinadas a casos em que a partícula e o observador se movem na mesma direção. Para o nosso caso, as equações serão as seguintes:

$$

$$\ updownarrow p = \ updownarrow \ overline p \\ \ leftrightarrow p = γ ([\ leftrightarrow \ overline p] + v \ overline E / c ^ 2) \\ E = γ (\ overline E + v [\ leftrightarrow \ overline p])$$

Essas equações serão mais simples do que parecem, pois, do ponto de vista de Petit, p não possui um componente que se move da esquerda para a direita e todo o pulso sobe ou desce. Portanto, Kostya observa os seguintes valores para Higgs:

$$

$$\ updownarrow p_0 = \ updownarrow \ overline p_0 = 0 \\ \ leftrightarrow p_0 = γ v \ overline {E_0} / c ^ 2 = (5/3) (4/5) 126 GeV / c = 168 GeV / c \ rightarrow \\ E = γ \ overline {E_0} = (5/3) 126 GeV = 210 GeV$$

E o fóton subindo

$$

$$\ updownarrow p_0 = \ updownarrow \ overline p_1 = 63 GeV / c \ uparrow \\ \ leftrightarrow p_0 = γ v \ overline {E_1} = (5/3) (4/5) 63 GeV / c = 84 GeV / c \ rightarrow \\ E = γ \ overline {E_0} = (5/3) 63 GeV = 105 GeV$$

Para o segundo fóton, as fórmulas são as mesmas, apenas seu componente vertical é direcionado para baixo. Observe que, para ambos os fótons E = pc, de acordo com o teorema de Pitágoras para o tamanho p de cada um dos pulsos, de acordo com a inserção na Fig. 10

$$

$$p_1 ^ 2 = (\ uparrow p_1) ^ 2 + (\ rightarrow p_1) ^ 2 \\ ou \\ (105 GeV / c) ^ 2 = (63 GeV / c) ^ 2 + (84 GeV / c) ^ 2$$

E, novamente, Kostya observa outros valores de energia e momento, em comparação com Petya e Masha. Mas para Kostya, energia e momento ainda são conservados. Kostya também observa que a massa de um sistema com dois fótons coincide com a massa de Higgs. Porque A parte vertical total do momento do sistema é zero, é mutuamente destruído. A parte horizontal do pulso do sistema é 168 GeV / s. A energia total do sistema é 210 GeV. É o mesmo que Masha observou, exceto que o momento do sistema aumentou, e não para a direita. Mas a direção do pulso não afeta a equação nº 1 '. Apenas sua magnitude desempenha um papel lá. Então, como Masha, Kostya vê que a massa do sistema de dois prótons é $$$126 GeV / c ^ 2$ igual à massa da partícula de Higgs primária.

Sumário

Então, vemos o que três observadores diferentes estão observando. Suas observações:

• variar sobre o que a energia e o momento de Higgs são,
• variar em termos de energia e momento de ambos os fótons,
• concordar com a conservação de energia e momento durante a deterioração,
• portanto, eles concordam que a massa do sistema é preservada,
• concorda que a massa do sistema é 126 GeV / c ² ,
• além disso, que a soma das massas dos objetos do sistema não é preservada, mas diminui de 126 GeV / c ² para zero.

E isso não é coincidência. Einstein, de experimentos anteriores, sabia que a energia e o momento são conservados; portanto, ele pesquisou e encontrou equações que preservam essa característica do mundo. Também no processo, ele descobriu que a massa do sistema deve satisfazer a equação nº 1 '.

Bônus: como é usado na busca de uma partícula de Higgs

Cientistas:

• observar colisões de prótons, como resultado do nascimento de dois fótons;
• calcular a massa de um sistema de dois fótons (no jargão técnico, isso é chamado de massa invariável de um par de fótons).

Quando, como resultado de um experimento, uma partícula de Higgs decai em dois fótons, não importa em que direção e velocidade a partícula se mova em relação ao laboratório, o sistema de dois fótons em que decai sempre terá uma massa igual à massa Partículas de Higgs que as produziram! Portanto, diferentemente dos processos aleatórios, que resultam em um sistema de dois fótons de massa aleatória, as partículas de Higgs sempre geram um sistema de dois fótons da mesma massa. Portanto, se as partículas de Higgs aparecerem nos resultados de um experimento e, às vezes, decaírem em dois fótons, veremos um pico nas decaimentos de Higgs que se elevam acima de um fundo suave de outros processos aleatórios. E assim aconteceu no experimento no LHC!