Como criar um poliedro impossível: matemática irreal do mundo real

A matemática nos dá uma imagem precisa das respostas quase exatas.

Usando papel grosso e fita transparente, Craig Kaplan recolhe um belo objeto arredondado semelhante à criação de Buckminster Fuller ou um novo e moderno tipo de bola de futebol. Consiste em quatro dodecágonos regulares (12 gons com os mesmos ângulos e lados) e 12 decágonos (poliedros de 10 lados) com 28 pequenas aberturas na forma de triângulos equilaterais. Há apenas um problema - esse número não pode existir. Esse conjunto de polígonos não coincide com os vértices e a figura não fecha.

O modelo Kaplan só funciona porque quando você o monta em papel, você tem pouca liberdade de manobra. Os lados podem dobrar-se quase imperceptivelmente. "A margem de erro resultante do trabalho no mundo real com papel significa que coisas que não deveriam ser possíveis são realmente obtidas", diz Kaplan, especialista em TI da Universidade de Waterloo, no Canadá.



Este é um novo exemplo de uma classe de objetos matemáticos inesperados que o matemático americano Norman Johnson encontrou nos anos 60. Johnson trabalhou na conclusão de um projeto iniciado há mais de 2000 anos por Platão - ele criou um catálogo de formas geométricas ideais. Da infinita variedade de figuras tridimensionais, apenas cinco podem ser criadas a partir dos mesmos polígonos regulares: tetraedro, octaedro, hexaedro, icosaedro, dodecaedro. Se você misturar polígonos regulares diferentes, poderá compor mais 13 figuras nas quais todos os polígonos encontram vértices - corpos arquimedianos - bem como prismas (dois polígonos idênticos conectados por quadrados) e "antiprismas" (dois polígonos idênticos conectados por triângulos equilaterais).

Em 1966, Johnson, enquanto trabalhava na Universidade de Michigan, descobriu mais 92 corpos, consistindo apenas de polígonos regulares, que agora [nos EUA] são chamados corpos de Johnson . E isso esgotou todas as possibilidades, comprovadas vários anos depois pelo matemático russo Viktor Abramovich Zalgaller , que trabalhou na Universidade Estadual de Leningrado. É impossível criar qualquer outra forma fechada a partir de polígonos regulares.

Mas durante um inventário do poliedro, Johnson notou algo estranho. Ele encontrou suas formas, compondo seus modelos de papelão e elásticos. Como existem muito poucos poliedros possíveis, ele esperava que novas formas aparecessem rapidamente. Se você começar a fazer caretas juntos, a figura deve necessariamente coincidir. Mas isso não aconteceu. “Ao montar uma pilha de polígonos, nem sempre era óbvio se eu tinha montado uma forma válida”, lembra Johnson.

Pode parecer que o modelo foi montado, mas "se você fizer os cálculos, acontece que isso não é inteiramente verdade", diz ele. Após um exame cuidadoso, verificou-se que o que parecia ser um quadrado não era exatamente um quadrado, ou os lados não eram muito planos. Seria possível aparar levemente as faces, e elas se encaixariam perfeitamente, mas não seriam mais polígonos regulares.

Com a intenção de calcular todos os números ideais, Johnson não deu importância a esses "acertos próximos". "Eu os deixei de lado e me concentrei no aceitável", diz ele. Mas essas figuras quase ideais não apenas atraíram a atenção de Kaplan e outros amantes da matemática, mas também se tornaram parte de uma seção maior da matemática quase ideal.

Não há definição exata de um hit "quase preciso". Regras estritas não funcionam em um mundo tolerante. Agora, Kaplan é guiado por um método aproximado na busca de números quase corretos: "um erro real e matemático inerente a um número é comparável a um erro prático decorrente do trabalho com materiais do mundo real e mãos imperfeitas". Em outras palavras, se você conseguiu montar um poliedro impossível - se é tão próximo do possível que você pode passar por um real - então esse será um número quase exato. Em outros ramos da matemática, resultados quase precisos são tão próximos do real que podem enganar ou surpreender você - uma espécie de piada matemática.

Algumas dessas esquisitices matemáticas não podem ser chamadas de nada além de simples diversão, enquanto outras podem ter significados profundos em matemática e física.

Os problemas antigos de formar um círculo e dobrar um cubo se enquadram na categoria de soluções quase corretas. Eles parecem tentadoramente abertos a encontrar a solução certa, mas no final se tornam impossíveis - como uma figura geométrica que parece fechada, mas não é. Alguns desenhos desenhados por Leonardo da Vinci e Albrecht Durer dobraram levemente os cantos, produzindo pentágonos quase regulares como reais.



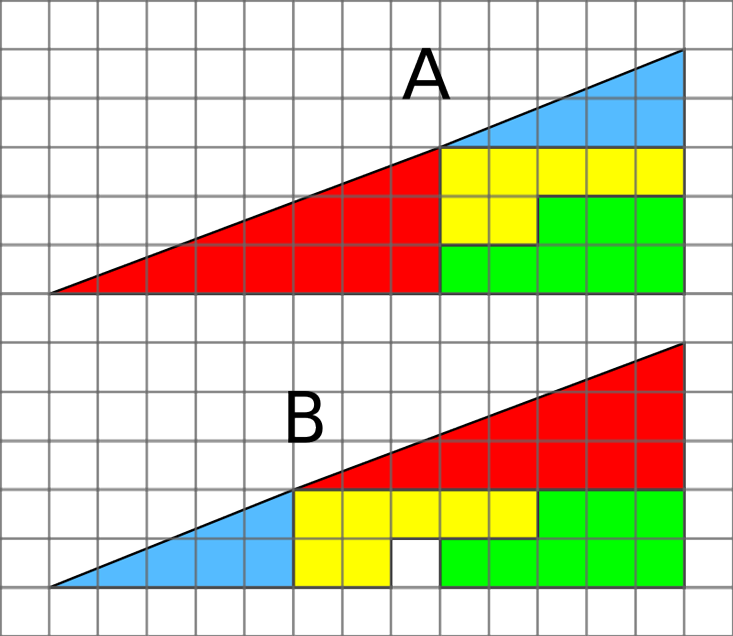
E há um enigma com um quadrado ausente. Na figura, um triângulo retângulo é cortado em quatro partes. Se você reorganizá-los, um espaço aparecerá nele. De onde ele veio? Esta também é quase a decisão certa. Nenhum dos triângulos é na verdade um triângulo. Seus hipotenos são distorcidos, e é quase impossível perceber, e é por isso que a ilusão é tão convincente.

A correspondência digital é uma das decisões de quase direita mais úteis na vida cotidiana. 2 ^{7/12 é} quase igual a 3/2. Por uma razão semelhante, o piano tem 12 teclas em uma oitava e no coração do sistema de música ocidental uniformemente temperado . Este é um compromisso entre os dois intervalos musicais mais importantes: uma oitava (frequência 2: 1) e um quinto (frequência 3: 2). Numericamente, não é possível dividir uma oitava para que todos os quintos sejam perfeitos. Mas você pode se aproximar o suficiente disso dividindo a oitava em 12 semitons, sete dos quais fornecerão uma frequência de 1.498. Para a maioria das pessoas, isso é suficiente.

Às vezes, acertos quase exatos ocorrem na matemática como se estivesse enganando a si mesma. No episódio dos Simpsons "Treehouse of Horror VI", o público interessado em matemática notou algo incomum: equação 1782 ¹² + 1841 ¹² = 1922 ¹² . À primeira vista, pode parecer que os escritores refutaram o Grande Teorema de Fermat, postulando que a equação x ⁿ + y ⁿ = z ⁿ não possui soluções inteiras para n> 2. Se você digitar esses números em uma calculadora de bolso, o resultado parecerá correto. Mas se você fizer cálculos com precisão que não está disponível para a maioria das calculadoras de bolso, a raiz do 12º grau do lado esquerdo da equação é 1921,999999955867 e não 1922, e Fermat pode ficar calmo. Deslizamento surpreendentemente pequeno - menos de 10 milhões de peças.

Mas esses acertos quase precisos não são apenas piadas. "Aqueles que mais me intrigam são os casos que sugerem a presença de algo mais significativo", diz John Baez, matemático da Universidade da Califórnia em Riverside. É o caso de uma quantidade que às vezes é chamada de constante de Ramanujan . Este ^número e ^{π √163} , igual a aproximadamente 262 537 412 640 768 743.9999999999999925, é surpreendentemente próximo do todo. Não podemos esperar que esses três números irracionais - e, π e √163 - de alguma forma se combinem e nos dê um número racional, sem mencionar o todo. Mas há uma razão pela qual eles combinam tão bem. "Não é apenas uma coincidência que não temos idéia", diz Baez. "Esta é a chave para as profundezas da matemática." A explicação exata é bastante complicada, mas baseada no fato de 163 ser o maior dos números de Hegner . Os expositores associados a esses números estão muito próximos dos números inteiros.

Ou faça uma conexão matemática conhecida como "Hipótese da lua monstruosa" (lua monstruosa). A história é a seguinte: em 1978, o matemático John Mackay fez uma observação trivial e igualmente interessante: 196 884 = 196 883 + 1. O primeiro número foi um coeficiente de um importante polinômio, j-invariante , e o segundo surgiu em conexão com um enorme objeto matemático da teoria dos grupos. chamado " monstro ". Muitas pessoas encolheram os ombros e foram além, mas essa observação interessou muitos matemáticos que decidiram estudá-la mais de perto. Eles encontraram uma conexão entre dois tópicos aparentemente não relacionados: teoria dos números e simetria dos grupos Monster. Essa conexão pode ter consequências ainda mais amplas, ainda não abertas, para outros tópicos. O físico Edward Whitten acredita que o grupo Monster pode ser associado à gravidade quântica e à estrutura espaço-temporal.

Os acertos matemáticos quase corretos mostram tanto a diversão quanto o poder da abordagem humana da matemática. Johnson, Kaplan e outros fizeram descobertas por tentativa e erro - estudando o campo como um biólogo andando pela floresta em busca de novas espécies. Mas, em matemática, é mais fácil realizar uma pesquisa sistemática. Por exemplo, Jim McNeill, que está interessado em matemática como hobby e coleciona uma coleção de hits quase corretos em seu site, e Robert Webb, um programador, criou um software para criar e estudar poliedros.

Acertos quase precisos vivem na linha desfocada entre idealista, matemática dura e nossos sentimentos condescendentes e práticos. Eles viram de dentro para fora a lógica da aproximação. Geralmente o mundo real é considerado uma sombra imperfeita do mundo de Platão. A perfeição da matemática subjacente se perde em sua implementação. Mas no caso de acertos quase precisos, o mundo real é a sombra perfeita do mundo imperfeito. A aproximação é "a aproximação errada da resposta correta", diz Kaplan, e "um acerto quase preciso é uma representação precisa de uma resposta quase precisa".

Dessa maneira, respostas quase precisas mudam a conexão entre matemáticos e físicos matemáticos com a natureza. "Sou grato pelas imperfeições do mundo real, porque elas me permitem alcançar um quase ideal trabalhando com objetos que são essencialmente imperfeitos", diz Kaplan. "Eles me permitem superar as limitações da matemática, graças à beleza de uma realidade quebrada."