Entendemos a física de partículas: 1) uma bola em uma mola, a versão newtoniana

1. Bola em uma mola, versão newtoniana
2. Uma bola quântica em uma mola
3. Ondas, visual clássico
4. Ondas, a equação clássica do movimento
5. Ondas quânticas
6. Campos
7. Partículas são quanta
8. Como as partículas interagem com os campos

Entender em termos gerais o básico da física de partículas - e esse é o nosso entendimento atual dos fenômenos mais elementares do Universo - não é tão difícil. Será mais fácil para você se você freqüentou uma escola de física e matemática ou completou o primeiro ano de faculdade. Mas se você lida com álgebra, trigonometria e (possivelmente, mas não necessariamente) os conceitos básicos de diferenciação e integração, poderá entender como os campos funcionam e como as partículas aparecem. Você só precisa aceitar minha palavra uma vez, em relação a um aspecto da mecânica quântica. Nesse caso, não darei fórmulas matemáticas, mas simplesmente mostrarei as respostas prontas. Mas depois que você aceitar esse aspecto, tudo ficará claro.


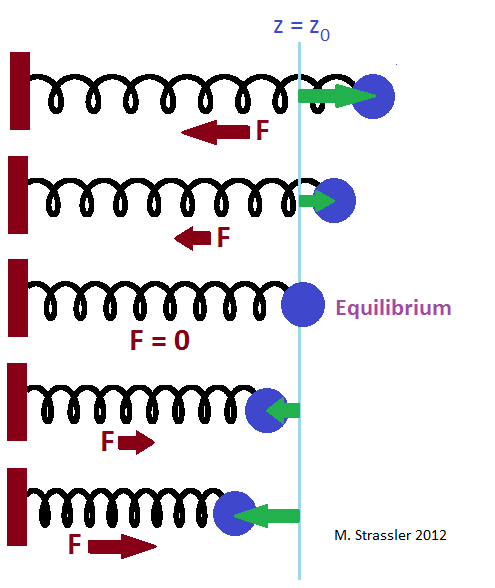Fig. 1

Para entender a física de partículas, na física da escola você precisa se lembrar de uma única coisa - como funciona uma mola. De fato, tudo o que salta, vibra, toca, chocalha e oscila, é um exemplo de mola.

Imagine que colocamos uma bola no final de uma primavera. Os movimentos da primavera e as equações que a descrevem são simples. Para começar, lembramos o básico do comportamento da mola, depois estudamos o comportamento da oscilação da bola. E, finalmente, para as mentes mais questionadoras, consideraremos as equações que levam a esse tipo de movimento.

Oscilador harmônico (também conhecido como bola em uma mola)

A bola na mola tem uma posição de equilíbrio; se você colocar a bola lá dentro e soltá-la, a mola não a empurrará em nenhuma direção e a bola permanecerá imóvel. Esta é a linha azul na fig. 1. Se você puxar a bola para longe da posição de equilíbrio (setas verdes), a mola puxará a bola para trás com força F (setas vermelhas). Quanto mais você puxa a bola, mais forte a mola a puxa para trás (pelo menos até que você a quebre ou quebre com pressão).

Movimento oscilante (pulando)

Chamamos a direção do movimento da bola de "direção z" e definimos o eixo z de modo que z = z ₀ corresponda à posição de equilíbrio da bola na mola. Suponha que puxemos a bola dessa posição, segure-a para que ela não se mova, para a posição z = z ₀ + A; então, em um determinado momento no tempo t = 0, nós o liberamos. A bola começará a pular aqui e ali - veja a fig. 2. A magnitude dos saltos - a amplitude das oscilações - é igual a A. Pode ser arbitrariamente grande ou pequeno; somente você escolhe quanto puxar a bola da posição de equilíbrio. Mas você não controla com que frequência os saltos de um lado para o outro - a frequência das oscilações - ocorrem. Acontece que é o mesmo, independentemente do valor de A. É determinado apenas pelas propriedades da bola e da mola, e não pelo que você faz.

Para fins científicos, é extremamente importante descrever observações através de uma fórmula matemática. A posição da bola z é uma função do tempo t, escrito por nós como z (t), assume a forma:

$$

$$z (t) = z_0 + A cos [2 \ pi \ nu t]$$

Onde, como sempre, cos é o cosseno, π é o número pi da geometria do círculo, z ₀ é a posição de equilíbrio da bola e A e ν (nu) são a amplitude e a frequência das oscilações. A função cosseno é oscilatória; portanto, esta fórmula descreve movimentos oscilatórios com amplitude A e frequência ν. Exemplos de movimento oscilatório de uma bola em uma mola com diferentes valores do desvio inicial e da amplitude total A são mostrados na Fig. 2, que também mostra que, para uma determinada bola em uma mola, a frequência ν não depende da amplitude A.

Impressão fina: amplitude e frequência são maiores que zero. Se A for negativo, a amplitude será –A. De fato, a amplitude é realmente | A |, ou seja, o módulo de magnitude.


Fig. 2

O que é muito importante lembrar sobre a amplitude e frequência da bola e da mola (na física pré-quântica clássica):
• a amplitude A pode ser selecionada qualquer;
• a frequência ν é determinada pela bola e mola e, para escolher uma frequência diferente, é necessário substituir a mola ou a bola.

O período de cada oscilação (quanto tempo leva para a bola avançar e recuar exatamente uma vez) será chamado T, e esse período é simplesmente o recíproco da frequência: T = 1 / ν. Se o período for de 5 segundos, a frequência será de uma vez a cada cinco segundos ou 1/5 de segundo (geralmente chamado 1/5 Hertz ou Hz).

Outra impressão pequena: em qualquer sistema real de mola e bola que você encontrará na vida cotidiana, o atrito levará ao fato de que A diminuirá gradualmente e, eventualmente, chegará a zero quando o movimento parar. As fórmulas que levam em consideração o atrito durante o movimento não são muito mais complicadas, mas não precisaremos delas. Portanto, sempre assumo que o atrito é pequeno, A diminui muito lentamente e podemos simplesmente usar fórmulas simplificadas que ignoram o atrito. Mas é importante saber: o atrito reduz A, mas, a menos que seja extremamente forte, não afeta ν e T! A frequência de oscilação permanece a mesma, mesmo com uma diminuição na amplitude. Portanto, a nota que a corda da guitarra produz depois que você a puxa não muda, mesmo quando o som resultante diminui gradualmente.

Mais uma coisa: existe uma bela fórmula para a energia armazenada em uma mola oscilante. É proporcional ao quadrado da amplitude e ao quadrado da frequência:

$$

$$E = 2 \ pi ^ 2 \ nu ^ 2 A ^ 2 M$$

Em parte, essa é a energia de movimento da bola (cinética) e, em parte, a energia de interação (potencial) armazenada na primavera, e quando a bola gira para frente e para trás, as frações dessas energias na energia total mudam constantemente. Mas a energia total E permanece constante.

Letras pequenas: ainda há a energia da massa da bola, Mc ² , mas não a rastreamos, porque está sempre lá, a mola se move com ela ou não.

A mesma fórmula de oscilação se aplica a quase tudo que treme ou salta apenas se esses saltos não forem muito grandes. Uma bola rolando ao longo do fundo da tigela; um carro pulando em amortecedores ruins; corda vibratória de um violino ou violão; barra de xilofone depois de bater nela; etc.

A equação do movimento vibracional (saltos matemáticos)

Agora, vamos lembrar as fórmulas básicas que nos explicam por que a bola na mola oscila.

Como mencionamos no início (Fig. 1), a bola na mola tem uma posição de equilíbrio, que chamamos de z = z ₀ . Suponha que em algum momento (puxamos a bola ou ela hesitou), ela esteja em uma posição diferente, z. Se z> z ₀ , isto é, se o deslocamento da posição de equilíbrio z - z _{0 for} maior que zero, a mola criará uma força direcionada na direção negativa z para puxar a bola de volta ao ponto de equilíbrio. Por outro lado, se z <z ₀ , ou seja, o deslocamento do equilíbrio z - z _{0 for} negativo, a mola criará uma força direcionada na direção positiva z, novamente para puxar a bola de volta ao ponto de equilíbrio. E quanto mais longe a bola estiver da posição de equilíbrio, mais forte a mola puxa. A força F criada pela mola está relacionada ao deslocamento da bola do equilíbrio pela equação

$$

$$F = - K (z - z_0)$$

Onde K é um valor positivo, dependendo de uma mola específica, chamada constante da mola.

Observe por que essa fórmula é verdadeira:

• Se a bola estiver na posição de equilíbrio, F = 0. A mola não cria força e, se a bola não se mover na posição de equilíbrio, ela permanecerá lá.
• Se o desvio for maior que zero, a força é negativa.
• Se o desvio for negativo, a força é positiva.
• Quanto maior o desvio, maior a força.

Em seguida, passamos à segunda lei do movimento de Newton, que afirma que, sob a influência da força F, uma bola de massa M se moverá com a aceleração a, onde F = M a. Substitua isso na fórmula e obtenha

$$

$$M a = - K (z - z_0)$$

ou

$$

$$a = - K / M (z - z_0)$$

Esta é uma equação quase necessária para nós, da qual a equação de oscilações pode ser derivada. Precisamos apenas lembrar a relação entre a e z. Para isso, é importante recordar a relação entre a e velocidade v e entre v e z. Essa proporção é uma das duas alterações ao longo do tempo:
• Velocidade é uma mudança de posição no tempo, v = dz / dt
• Aceleração é uma mudança na velocidade ao longo do tempo, a = dv / dt

Adicione e obtenha

$$

$$a = d (dz / dt) / dt = d ^ 2z / dt ^ 2$$

Aceleração é a mudança no tempo de uma mudança de posição ao longo do tempo.

Podemos reescrever nossa equação da equação do movimento

$$

$$d ^ 2z / dt ^ 2 = - K / M (z - z_0) \ quad (*)$$

Onde z é uma notação curta para z (t). E agora podemos verificar que o movimento vibracional z (t) = z ₀ + A cos [2 π ν t] será uma solução para essa equação de movimento. Precisamos primeiro calcular a velocidade de uma partícula como uma mudança em sua posição no tempo:

$$

$$d / dt (z_0 + A cos [2 \ pi \ nu t]) = - (2 \ pi \ nu) Um pecado [2 \ pi \ nu t]$$

(dz ₀ / dt = 0, uma vez que a posição de equilíbrio z ₀ não muda com o tempo ed / dt (cos wt) = -w sin wt); e então calculamos a aceleração da partícula como uma mudança na sua velocidade ao longo do tempo:

$$

$$d / dt [- (2 \ pi \ nu t)] = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t]$$

(desde d / dt (sen wt) = w cos wt). Como resultado

$$

$$d ^ 2z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t] = - (2 \ pi \ nu) ^ 2 (z - z_0)$$

Onde, no último passo, usei a fórmula z (t) = z ₀ + A cos [2 π ν t] para movimento oscilatório. A equação final é igual à nossa equação de movimento [ $$$d ^ 2z / dt ^ 2 = - K / M (z - z_0)$], dado que (2 π ν) ² = K / M, se a frequência de oscilação for

$$

$$ν = \ frac {\ sqrt {K / M}} {2 \ pi}$$

E, de fato, descobrimos que nossa equação de movimento implica que a mola irá oscilar com a frequência indicada, que essa frequência não depende de A - depende apenas das propriedades da mola (K) e da bola (M) - e que, independentemente da quantidade A para a equação existe uma solução. Portanto, podemos escolher qualquer A, dependendo de quão longe puxamos a bola da posição de equilíbrio antes de liberá-la.

Ressonância

A ressonância é um dos fenômenos naturais mais importantes, tanto na vida cotidiana, onde desempenha um papel em muitos aspectos da tecnologia e na música, quanto nos processos básicos do mundo físico, especialmente na física de partículas.

Primeiro, lembre-se de como o balanço funciona. Um balanço, como uma bola em uma mola ou qualquer pêndulo, é um oscilador - ele oscila para frente e para trás com uma certa frequência, o que não depende da amplitude do balanço. No caso de um balanço, essa afirmação permanece verdadeira até que a amplitude seja muito grande. Provavelmente, você sabe por experiência que, para elevar uma criança mais alta, é necessário empurrar a oscilação para frente uma vez por ciclo, para que a amplitude da oscilação esteja constantemente aumentando. Se você empurrar o balanço para frente várias vezes por ciclo, ou uma vez a cada dois ciclos e meio, às vezes você aumentará a amplitude do balanço e, às vezes, a reduzirá. Obviamente, há algo de especial em alinhar a frequência com a qual você empurra o balanço com a frequência natural do próprio balanço.

Da mesma forma, se a própria criança sabe como balançar o balanço, ela sabe que precisa balançar as pernas ao mesmo tempo que a frequência natural do balanço para aumentar a amplitude do balanço. Gire de uma maneira diferente e a amplitude não aumentará.



Você pode rastrear como isso acontece com a bola na primavera. Olhe para a foto. À esquerda, há uma bola oscilando de um lado para o outro em torno de uma posição de equilíbrio. Ele hesita, sem choques externos. Oscila com a frequência natural da primavera ν. A frequência é √ K / M, onde K é a força da mola, M é a massa da bola.

À direita na fig. você pode ver o que acontece com outra bola preta, a massa igual à primeira, na mesma mola, que é empurrada com a força F (sua magnitude e direção são mostradas pela seta vermelha), que oscila com uma frequência ν _F diferente de ν. Uma bola preta se comporta como um balanço que empurra muito raramente; eles se moverão em um padrão complexo e não subirão alto. Na fig. pode-se ver que a bola não oscila muito suavemente e a amplitude das oscilações é pequena. Você pode ver como ele “tenta” oscilar com uma frequência natural, embora seu movimento geral seja repetido com uma frequência ν _F.

Então a figura mostra o caso em que a força oscila com uma frequência νF, que é muito maior que a frequência ν. Novamente, você pode ver como ele “tenta” oscilar com uma frequência natural, mas ele não consegue fazer isso com uma grande amplitude, pois uma força que oscila rapidamente pode pressioná-lo ou contra o movimento, aumentando ou diminuindo a amplitude. .

E no final, o caso é mostrado quando a força oscila com a frequência natural da mola, ν _F = ν. A bola reage de maneira muito diferente: a amplitude das oscilações cresce constantemente, e a bola preta oscila com tanta facilidade e suavidade quanto a bola branca à esquerda, mas com um aumento na amplitude. Isto é uma ressonância.

Como resultado: se ν _F difere de ν - se a força não permitir que a bola entre na ressonância - ela se moverá, mas com relutância, e seu movimento será muito diferente do natural, a partir de uma simples oscilação com frequência ν. Pelo contrário, se a frequência da força corresponde à natural - se a força introduz a bola em ressonância -, então a força empurra a bola com muito mais eficácia, e o movimento resultante é mais impressionante. Nós sabemos disso intuitivamente; empurrando o balanço com uma frequência natural, a criança (ou pai) oscila cada vez mais alto.

Entre os aspectos importantes da ressonância na física de partículas está o fato de que, em certas circunstâncias, as partículas podem ser geradas devido a um mecanismo muito semelhante: após uma colisão de duas partículas, uma força é obtida exatamente com a mesma frequência necessária para criar uma terceira.

Da próxima vez: bola quântica em uma mola

Esse é o comportamento de uma bola em uma mola na física clássica pré-quântica. A mecânica quântica muda muitos conceitos , mas o mais importante é este: ainda podemos escolher A, mas A não pode ser de nenhum tamanho. Pode levar apenas certos valores proporcionais à raiz quadrada de números inteiros.