Entendemos a física de partículas: 3) ondas, forma clássica

1. Bola em uma mola, versão newtoniana
2. Uma bola quântica em uma mola
3. Ondas, visual clássico
4. Ondas, a equação clássica do movimento
5. Ondas quânticas
6. Campos
7. Partículas são quanta
8. Como as partículas interagem com os campos

Tendo lidado com as equações das oscilações - descrevendo quase tudo o que pula, vibra, rola para frente e para trás, como uma bola em uma mola -, podemos passar para o fenômeno natural igualmente comum, as ondas. As ondas estão por toda parte: som e luz, terremotos, ondulações na superfície da lagoa, etc.


Fig. 1

Mas antes disso, aviso que o termo "onda" pode ser enganador, pois na física não significa o mesmo que em inglês. Na física, isso não significa o que normalmente chamamos de onda na beira do oceano - uma crista e uma cavidade. Na física, as ondas são uma sequência de ondas, vários cumes e vales que se movem juntos na mesma direção. Em uma onda da forma mais simples, todas as cristas têm a mesma altura e estão espaçadas uma distância uma da outra. Vamos considerar exatamente esse caso.

As ondas são um fenômeno marcante, se você pensar bem. Imagine que você e seu amigo pegaram uma corda comprida e a puxaram com força na sala (fig. 2). Imagine que seu amigo conversou várias vezes com uma ponta da corda (verde). Uma onda aparecerá no final da corda e atravessará a sala até o final da corda (vermelho).


Fig. 2

Isso é incrível. Quero dizer - é realmente incrível, forte e crítico para tudo em nosso universo, incluindo você pessoalmente. Olha o que aconteceu. Nenhum dos objetos físicos se moveu da esquerda para a direita - antes de seu amigo começar a mover o final da corda, ele era esticado pela sala e, no final, depois que o final da corda para de vibrar e a onda desaparece, a corda permanece esticada por todo o corpo quarto, como era. E ainda! Energia e informação circulavam pela sala. A onda no caminho transfere a energia gasta por seu amigo nas vibrações do cabo - e carrega em sua forma informações sobre quantas vezes e com que rapidez ele o puxou - para você, onde faz sua mão tremer. E, nesse caso, ela até apertará sua mão tantas vezes e nessa sequência. Uau! Nenhum objeto físico se moveu pela sala, e energia e informação se moveram.

Ou espere. Mas não devemos considerar a onda como um objeto físico? Tão físico quanto a própria corda?

Lembrando desta questão mais profunda, passemos a um pequeno número de fórmulas matemáticas necessárias para descrever a aparência e o comportamento da onda e, em seguida, use um pouco mais de matemática para escrever as equações cujas soluções são as ondas. Isso é semelhante ao que fizemos para uma bola de primavera clássica.

Fórmula para uma onda infinita em um determinado momento

Esta série de artigos imediatamente após a bola na mola vai para as ondas porque a onda é uma espécie de oscilador duplo. Flutua no tempo e no espaço. Designaremos o tempo com a letra "t" e o espaço com "x".

Preste atenção na fig. 3. Ele descreve uma onda que se estende em ambas as direções por uma grande distância, na qual se encaixam muitas cristas e depressões. Isso é diferente da onda na fig. 2, que tem apenas alguns sulcos e depressões. Mas essa diferença é irrelevante - na Fig. 2 Eu precisava ilustrar para o que a forma de onda exata não importava; Agora vamos nos concentrar na fórmula matemática das ondas, e é muito mais fácil fazê-lo se a onda tiver um grande número de cristas e depressões do mesmo tamanho. Além disso, este caso será muito útil para entender como a mecânica quântica afeta o comportamento das ondas.



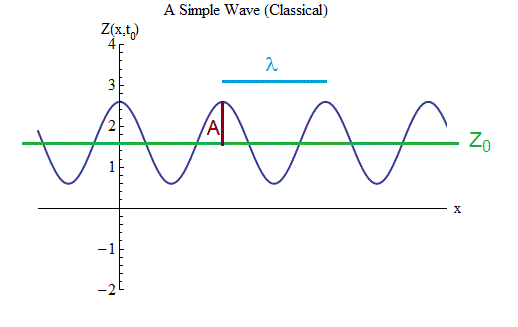
Fig. 3

Primeiro, precisamos determinar a notação e escrever uma fórmula descrevendo o movimento e a forma de onda na Fig. 3, como fizemos para a bola na primavera.

O gráfico mostra a magnitude da onda Z em função do espaço em um determinado período de tempo t = t ₀ - registramos isso como Z (x, t ₀ ). Seguindo a onda no espaço, vemos que ela oscila para frente e para trás, e Z periodicamente aumenta e diminui. A qualquer momento, a onda oscila no espaço.

Observe que Z não precisa estar relacionado à distância física. Pode ser a altura da corda, como na fig. 2, ou pode ser algo completamente diferente, por exemplo, a temperatura do ar em um determinado ponto no espaço e no tempo ou a orientação de um átomo magnético em um determinado local de um ímã. Mas x ainda representa a distância física e t é o tempo.

O tiro dessa onda, Z (x, t ₀ ), tem três propriedades interessantes, duas das quais também se aplicam a uma bola em uma mola.

1. Existe um valor de equilíbrio Z ₀ no meio, entre o maior valor de Z na crista e o menor valor de Z na depressão. Na maioria das vezes estudamos ondas para as quais Z ₀ = 0, porque geralmente o valor Z ₀ não importa - mas nem sempre.
2. A onda possui uma amplitude A, um valor pelo qual Z muda do valor de equilíbrio para o topo de cada cordilheira ou pelo mesmo valor para o fundo de cada depressão.
3. A onda tem um comprimento - a distância λ entre as cristas adjacentes, ou, o que é o mesmo, entre as calhas vizinhas ou, o que é o mesmo, duas vezes a distância entre a crista e a calha adjacentes. Descreve as oscilações no espaço da mesma maneira que um período (igual a 1 / frequência) descreve a oscilação no tempo de uma bola em uma mola.


Fig. 4

O que nos lembra o formulário na Fig. 3? Parece um gráfico da função seno ou cosseno - veja a fig. 4, onde cos (w) é plotado em w. Cos (w) é uma função oscilante, que tem uma posição de equilíbrio óbvia em zero, sua amplitude é 1 e o comprimento de onda é 2π. Como ir da fig. 4 à fórmula da onda na Fig. 3? Primeiro, multiplicamos cos (w) por A, para que a amplitude seja igual a A. Em seguida, adicionamos Z ₀ a toda a fórmula para alterá-la para o valor de equilíbrio desejado (se A = 0, então não há oscilação e tudo fica no ponto Z = Z ₀ ) E finalmente, substitua w por 2πx / λ, uma vez que cos (w) possui cristas em w = 0 e w = 2 π, portanto, em cos (2πx / λ), as cristas terão em x = 0 e x = λ. Todos juntos nos dá

$$

$$Z (x, t_0) = Z_0 + A cos (2 \ pi x / \ lambda)$$

Esta é quase a mesma fórmula que descreveu o movimento de uma bola em uma mola no tempo:

$$

$$z (t) = z_0 + A cos (2 \ pi \ nu t) = z_0 + A cos (2 \ pi t / T)$$

Onde ν é a frequência de oscilação e T = 1 / ν é o período de oscilação. Veja a analogia: um período refere-se ao tempo e um comprimento de onda refere-se ao espaço.

Mais uma nota antes de continuarmos. Eu também poderia escrever:

$$

$$Z (x, t_0) = Z_0 + A cos (- 2 \ pi x / \ lambda)$$

Como cos [w] = cos [-w]. O fato de podermos substituir facilmente o menos na fórmula da forma de onda será importante mais tarde.

Fórmula para uma onda sem fim em um local específico

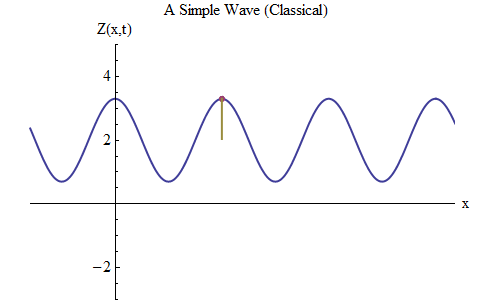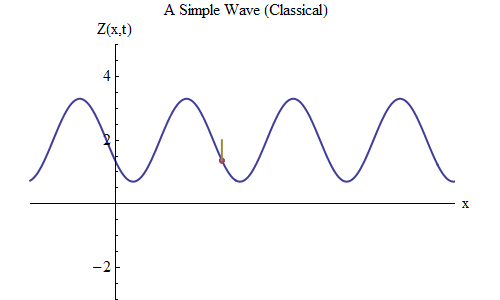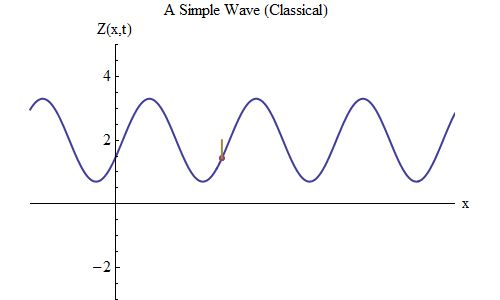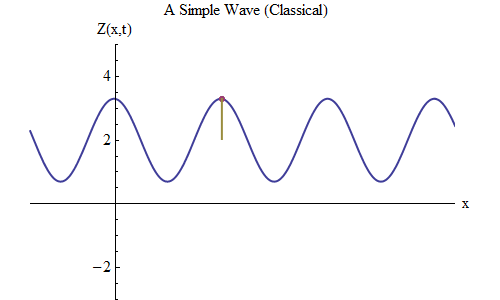Fig. 5

Agora vamos fazer outra pergunta: vamos ver como a onda muda com o tempo, acompanhando um certo ponto da corda, e como ela se comporta e se move. Isso é mostrado na fig. 5: ali designei um ponto específico x ₀ , que no momento t ₀ está no topo. A onda se move para a direita e segue o tamanho da onda Z no ponto x ₀ , mudando no tempo: Z (x ₀ , t). E você verá imediatamente que a altura da onda em um determinado ponto se comporta exatamente como uma bola em uma mola! Portanto, ela terá exatamente a mesma fórmula que uma bola em uma mola, em função da frequência ν ou do período T = 1 / ν, em que T é o tempo entre o momento em que a onda em x ₀ está na crista e o momento em que ela se aproxima da crista novamente na próxima vez.

$$

$$Z (x_0, t) = Z_0 + A cos (2 \ pi \ nu t) = Z_0 + A cos (2 \ pi t / T)$$

Fórmula completa de ondas infinitas

Agora precisamos de uma fórmula para Z (x, t) que descreva a onda representada na Fig. 3 e 5 (ou qualquer similar) nos pontos x a qualquer momento t. A resposta correta é:

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

Inclui as duas fórmulas, para um ponto fixo no tempo e para um ponto fixo no espaço.

Observe o sinal de menos na frente de x. Eu mencionei que na fórmula para Z (x, t ₀ ) você pode substituir um menos à vontade. Com um sinal de menos na frente de x e um sinal de adição na frente de t, a fórmula descreve uma onda se movendo para a direita, como nas animações. Para verificar isso, observe que quando t / T - x / λ = 0, a onda será uma crista porque cos [0] = 1. Quando t = 0, no ponto x = 0, a crista. Mas se avançarmos um pouco t, digamos, por T / 10, a crista estará no ponto x = λ / 10, à direita do local em que estava em t = 0 - portanto, a crista (e toda a onda) se move para a direita.

O que mudará se você colocar um mais em vez de um menos na fórmula de Z (x, t)? Então a crista estará em t / T + x / λ = 0 e, neste caso, em t = T / 10, a crista estará em x = -λ / 10, à esquerda do local onde estava em t = 0 - o que significa , agora a onda se move para a esquerda (fig. 6).


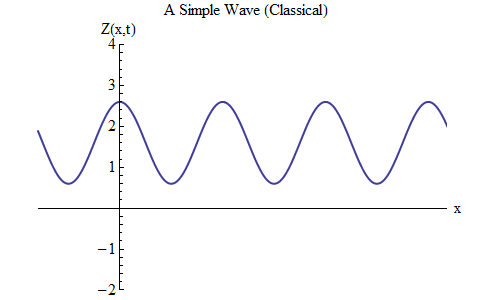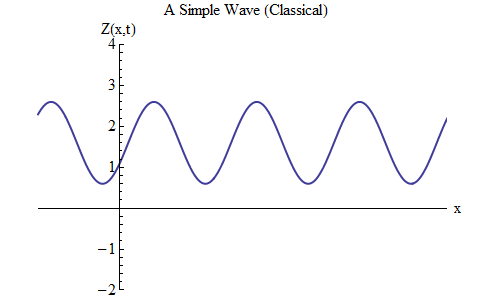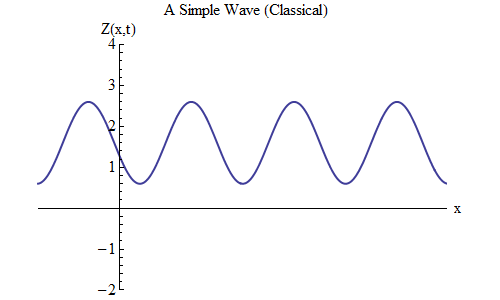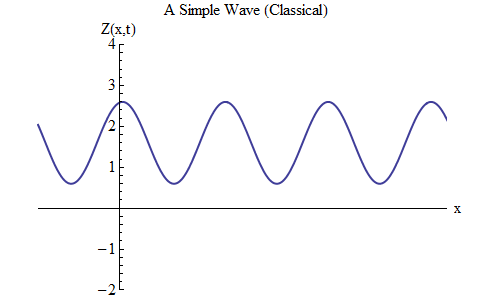Fig. 6

As ondas, que são funções de x e t, podem se mover em qualquer direção; portanto, precisamos apenas escolher a fórmula certa para a onda especificada. De um modo geral, quando trabalhamos com ondas que podem se mover não apenas ao longo de uma dimensão espacial x, mas ao longo das três coordenadas x, ye z, essas ondas podem se mover em qualquer direção, e precisaremos escolher a fórmula correta com base na direção movimento de onda.

Impressão fina: podemos colocar um sinal de menos na frente de t, e não antes de x. Mas + t, + x é o mesmo que –t, -x, porque isso será equivalente a multiplicar a fórmula inteira dentro do cosseno por -1, e cos [w] = cos [-w]. Portanto, + t, + x e -t, -x dão uma onda que se move para a esquerda e + t, -x e -t, + x dão uma onda que se move para a direita.

Equação de Onda

Agora, como no caso de uma bola em uma mola, quando encontramos pela primeira vez uma fórmula para o movimento oscilatório da bola e depois analisamos a equação do movimento, para a qual essa fórmula era uma solução, faremos o mesmo aqui. Encontramos uma fórmula para a forma e o movimento da onda. Qual equação de movimento entre as soluções tem essa fórmula? Aprendemos no próximo artigo.