Entendemos a física de partículas: 6) campos

1. Bola em uma mola, versão newtoniana
2. Uma bola quântica em uma mola
3. Ondas, visual clássico
4. Ondas, a equação clássica do movimento
5. Ondas quânticas
6. Campos
7. Partículas são quanta
8. Como as partículas interagem com os campos

De fato, entramos no território do campo há algum tempo, eu apenas não o avisei - eu queria me concentrar nas ondas que surgem nesses campos. Descrevendo como as ondas se comportam, expressamos sua forma e dependência do tempo usando a função Z (x, t). Bem, Z (x, t) é um campo. Esta é uma função do espaço e do tempo com uma equação de movimento que determina seu comportamento. Uma função de movimento adequada seria tal que, se Z aumentar ou diminuir em um determinado ponto, Z diminuirá ou aumentará em pontos vizinhos um pouco mais tarde. Esse recurso permite que as ondas estejam entre as soluções da equação.

Neste artigo, examinaremos alguns exemplos de campos Z (x, t) cujas equações de movimento permitem a presença de ondas. A interpretação física desses campos será muito diferente. Eles descrevem as diferentes propriedades de diferentes materiais. Mas as equações que satisfazem e as ondas que demonstram satisfazem matemática muito semelhante e se comportam de maneira semelhante, apesar de suas diferentes origens físicas. Este será um ponto muito importante no futuro.

E então fazemos algo radical - considere os campos no contexto da teoria especial da relatividade. Como Einstein mostrou, se você corrigir o espaço e o tempo e forçá-los a liderar não da maneira que as pessoas esperam, obterá um novo tipo de campo - de modo que sua interpretação física não é uma propriedade de qualquer outra coisa, mas um objeto físico independente.

Campos comuns que descrevem coisas comuns

O campo Z (x, t) pode representar muitas quantidades físicas diferentes. Por exemplo:
• A altura da corda se estendia pela sala.
• a altura da água no rio.
• A densidade do cristal ou gás.
• A posição dos átomos em um ímã.
• velocidade do vento.
• Temperatura, densidade ou pressão do ar.

Em qualquer um desses casos, há um campo Z (x, t): um campo de altura, um campo de densidade, um campo de orientação, um campo de vento e um campo de temperatura. Seu valor na forma de uma função do espaço e do tempo nos diz a altura, densidade, orientação, velocidade do vento ou temperatura de um determinado meio - uma corda, rio, cristal, gás, ímã, ar - em todos os lugares a qualquer momento. Sua equação de movimento mostra como Z (x, t) pode se comportar em princípio. Também mostra como prever o comportamento de Z (x, t) no futuro, se conhecermos exatamente seu comportamento no presente e no passado.

Em cada exemplo, há um campo e um ambiente, e não devemos confundir o campo com o ambiente. O campo simplesmente descreve e caracteriza uma das muitas propriedades do ambiente correspondente. Ambientes absolutamente diferentes podem ter campos de comportamento muito semelhantes com ondas muito semelhantes - ainda o veremos.

Mais uma vez vou esclarecer um ponto que muitas vezes causa mal-entendidos. Em geral, um campo pode não ter nada a ver com a distância física no espaço. Sim, nos artigos 3 e 4, usei o exemplo de um boi em uma corda para ilustrar o que Z (x, t) pode ser, porque é bonito e intuitivo. Também plotei gráficos Z (x, t) para ondas. Isso pode lhe dar a falsa impressão de que Z (x, t) está sempre associado a ondas que fazem com que um objeto físico (como uma corda) mova uma distância Z em uma direção perpendicular ao eixo x. Mas não é assim, como três de nossos quatro exemplos nos demonstrarão.

Campo de altura da corda

Primeiro, considere nosso exemplo inicial de ondas, uma corda oscilante. Nesse caso, o papel de Z (x, t) é o campo de altura, que chamamos de H (x, t). Ele nos diz a altura da corda em cada ponto no espaço no eixo x que corre ao longo da corda a qualquer momento t. Se o cabo estiver na altura de equilíbrio H ₀ , então H (x, t) = H ₀ . O campo de altura é uma constante no espaço e no tempo. Se uma onda simples se mover através dela, o campo de altura será descrito pela famosa fórmula de ondas de artigos anteriores.

Se conhecemos H (x, t), sabemos a altura da corda em todos os pontos no espaço e no tempo. Se soubermos o que a corda está fazendo agora e o que vem fazendo recentemente, usando a equação do movimento, podemos prever o que ela fará no futuro. Isso nos diz pouco sobre a própria corda. O campo de altura nos dá apenas o que seu nome indica: a altura da corda. Uma corda é um meio físico cuja altura é representada como um campo H (x, t); não nos diz nada sobre a cor da corda, sua espessura, tensão, material etc.

Na fig. 1 Fiz para você uma animação de uma onda em um campo de altura que vai da esquerda para a direita. Pode parecer que eu pintei a mesma coisa duas vezes, primeiro em verde e depois em laranja. Mas isso não é a mesma coisa. A curva laranja é a própria corda, movendo-se no espaço físico. Uma curva verde é um gráfico que representa o que está acontecendo com H (x, t), independentemente do que H (x, t) (ou seja, altura) significa ou que tipo de ambiente é. E somente neste caso, o gráfico verde parece exatamente o mesmo que está acontecendo no mundo físico. Mas em todos os outros casos, não será assim.


Fig. 1

Campo Deslocamento da Malha

Suponha que tenhamos um meio constituído por um cristal com átomos distribuídos uniformemente a distâncias iguais entre si. Eu os desenhei na foto. 2 em uma dimensão - você pode imaginar situações semelhantes com três dimensões, mas por enquanto isso seria uma complicação desnecessária. Também marquei cada décimo átomo em vermelho para facilitar o rastreamento do movimento deles. E também exagerei muito a distância entre os átomos - imagine que entre cada dois pontos vermelhos haja vários milhões de átomos, não 10.

Observamos o campo de deslocamento D (x, t), que nos diz quanto no momento t o átomo, geralmente localizado no ponto de equilíbrio x, se moveu desse ponto na rede. Isso significa que, no caso de um estado estático do qual a animação começa, o campo está em toda parte zero, D (x, t) = 0, pois todos os átomos estão em sua posição usual. Então, na animação, os átomos individuais começam a oscilar para frente e para trás, e seu movimento, em geral, se propaga na forma de uma onda que vai da esquerda para a direita. No topo da figura, o gráfico do campo de deslocamento da rede D (x, t) mostra como o campo se comporta durante a passagem da onda. Observe que os campos na Fig. 1 e 2 se comportam de maneira semelhante, embora a interpretação física dos campos seja muito diferente.


Fig. 2

Campo de orientação magnética

O que é um ímã permanente? Consiste em um conjunto de átomos, cada um dos quais serve como um minúsculo ímã com um minúsculo campo magnético, e todos eles estão alinhados para que juntos criem um grande campo magnético. O ímã é mostrado na fig. 3, e nele cada átomo é direcionado para cima. Nesse caso, o campo de orientação Θ (x, t) nos diz quanto tempo t o átomo no ponto x se desvia da vertical. Θ, em resumo, será o ângulo entre o ímã de cada átomo e a vertical. A animação na fig. 3 mostra uma onda em um ímã no qual as direções dos ímãs atômicos oscilam para a esquerda e para a direita. Um gráfico Θ (x, t) é mostrado acima do ímã verde; e novamente ele parece exatamente o mesmo que nos casos anteriores.

Campo de pressão de ar

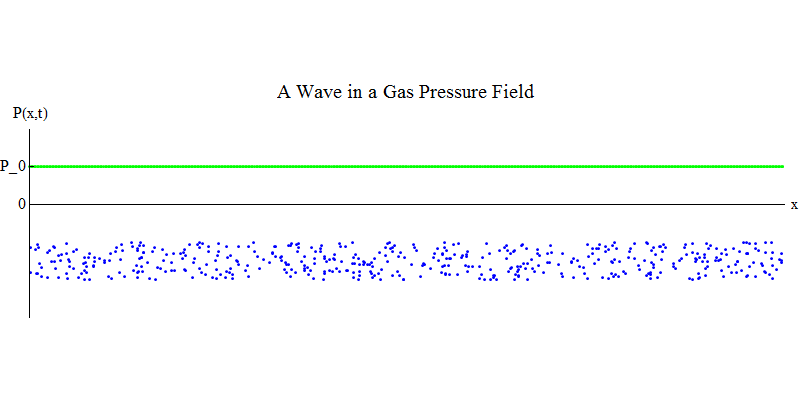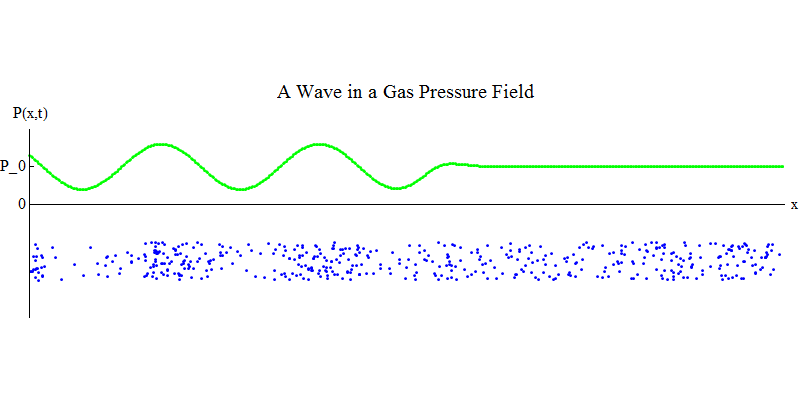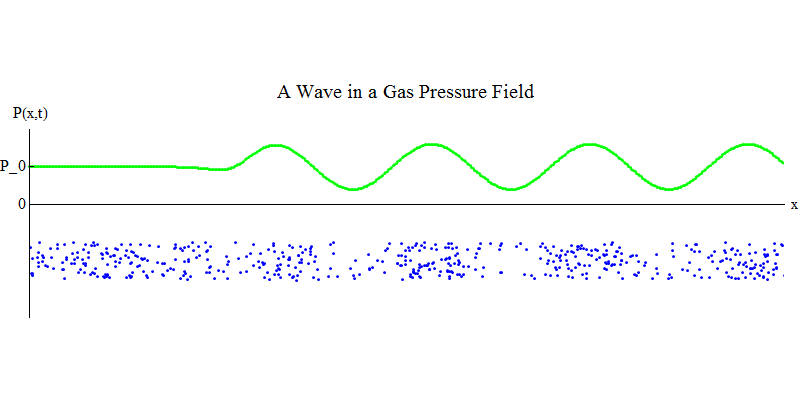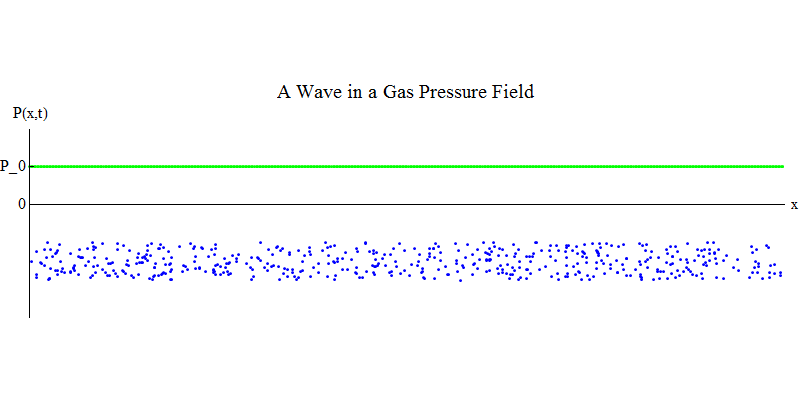
Considere um gás molecular em um tubo longo. Ao longo do tubo será a dimensão x. As moléculas de gás se moverão quase aleatoriamente, colidindo com as paredes do tubo e entre si. Em equilíbrio, a densidade (o número de moléculas em um determinado volume) e a pressão P (x, t) (a força que atua na superfície de uma pequena bola que apareceu no ponto x no tempo t) são constantes. Mas as ondas sonoras que passam pelo gás farão com que a pressão e a densidade oscilem, como mostrado na fig. 4. A densidade e a pressão aumentam e diminuem periodicamente. As moléculas se movem para frente e para trás, embora em média não se movam, mas ao mesmo tempo a onda e sua energia se movem da esquerda para a direita através do gás. O gráfico P (x, t) parece novamente muito semelhante aos anteriores.

Lições importantes

O que podemos aprender com quatro exemplos que mostram ondas da classe 0? (A equação do movimento tem uma quantidade, cw, e todas as ondas no campo correspondente se movem com a velocidade cw. Campos diferentes da classe 0 terão valores diferentes de cw). Podemos descobrir que o mesmo comportamento de campo pode emergir de campos fisicamente diferentes existentes em ambientes fisicamente diferentes. Apesar de sua origem diferente, as ondas no campo de altura, no campo de deslocamento da treliça, no campo de orientação magnética e no campo de pressão de gás parecem idênticas do ponto de vista dos campos. Eles satisfazem o mesmo tipo de equação de movimento e a mesma relação numérica de frequência e comprimento de onda.

Letras pequenas: a rigor, se você criar ondas com um comprimento suficientemente curto, ainda poderá distinguir o comportamento de diferentes mídias. Assim que os comprimentos de onda forem iguais à distância entre os átomos da corda, ou cristal ou ímã, as equações de onda que as ondas satisfarão serão mais complexas do que as escritas por nós, e seus detalhes diferenciarão a mídia uns dos outros. Mas frequentemente em experimentos práticos, nem chegamos perto de observar tais efeitos.

O resultado disso é que o estudo das ondas e seus quanta relacionados aos campos não indica necessariamente o que serve como meio, ou qual é a interpretação física do campo - quais são as propriedades do meio. E mesmo que você saiba de alguma forma que este é um campo de um determinado tipo - por exemplo, um campo de pressão - você normalmente ainda não será capaz de dizer pelo seu comportamento qual pressão ele representa. Tudo o que você pode aprender estudando as ondas é se o campo pertence à classe 0 ou classe 1 e qual é o valor de cw; ou descubra que o campo pertence a outra classe.

Em alguns casos, isso é muito ruim; o campo transmite apenas informações parciais sobre o ambiente. Isso às vezes é bastante conveniente; o campo é uma coisa mais abstrata e universal do que o material físico que ele descreve.

Portanto, o campo não define o ambiente e seu comportamento geralmente não depende dos detalhes e propriedades do ambiente. Por causa do que a questão surge.

Poderia existir um campo físico - com ondas constituídas por quanta se movendo no espaço e transferindo energia - sem nenhum meio de sustentá-lo?

Campo sem meio?

Você não pode ouvir uma música sem um cantor. Mas a música tem algum tipo de existência independente; soa diferente, dependendo de quem a canta, mas ao mesmo tempo há algo inerente à música, alguma qualidade abstrata, graças à qual ela sempre pode ser reconhecida. Essa entidade abstrata é a melodia da música. Podemos discutir, estudar, aprender uma melodia, gravá-la com uma gravação musical, sem sequer ouvi-la tocada pelo cantor. Muitos de nós podem até cantarolá-lo em nossas cabeças. De alguma forma, existe uma melodia mesmo que ninguém esteja tocando uma música.

Se em todos os exemplos dados por mim e em todos os exemplos que posso dar, e que serão intuitivamente claros para você, o campo descreve a propriedade, como um campo pode existir sem um ambiente? Mas, de alguma forma, os campos são independentes de seu ambiente, pois muitos campos diferentes podem se comportar da mesma maneira, apesar de descreverem muitas propriedades diferentes de ambientes completamente diferentes. Portanto, provavelmente é possível abstrair o campo do ambiente.

De fato, isso não é apenas possível, parece necessário. No mínimo, é necessário não ter um meio ou ter um ambiente que não possa ser criado a partir da matéria comum, que é fundamentalmente diferente de todos os meios de comunicação que examinamos - na medida em que funciona de tal maneira (de acordo com todos os experimentos) que ele não existe .

Um dos vários elementos radicais da teoria da relatividade especial de Einstein, de 1905, foi a idéia de que, para as ondas de luz - durante décadas consideradas ondas em campos elétricos e magnéticos (ondas eletromagnéticas) e se movendo na mesma velocidade no espaço vazio - não há meio. Existem apenas campos.

O meio hipotético foi chamado de "éter"; Einstein argumentou que tal coisa não existe e escreveu um conjunto de equações para as quais não era necessário. Observo que ainda existe um debate (geralmente mais filosófico do que físico) sobre se você precisa ou não imaginar a existência de algum ambiente estranho que é muito diferente da matéria comum. Até o momento, não há evidências que exijam sua disponibilidade.

Os elementos-chave da versão da relatividade de Einstein (em contraste com as versões de Galileu e Newton) foram os seguintes:

• Espaço e tempo não são o que você pensa que são. Observadores diferentes, movendo-se uniformemente entre si, divergem em suas estimativas do comprimento dos objetos e nos intervalos de tempo entre os eventos (e essas discrepâncias podem ser medidas com precisão).
• Existe um limite de velocidade universal, s; qualquer observador que mede a velocidade de um objeto em relação a ele descobrirá que essa velocidade é menor ou igual a s.
• Nesse mundo, certos campos - “campos relativísticos” - podem existir sem um meio e satisfazem equações especiais de movimento. O campo relativístico mais simples satisfaz as equações de movimento das classes 0 ou 1, com a velocidade de onda cw mencionada na equação de movimento assumindo o valor c.

Em suma, existem campos relativísticos da classe 0 que satisfazem a equação

$$

$$Classe 0: \; D ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

A luz e todas as ondas eletromagnéticas são o exemplo mais famoso, mas não o único - portanto, "c" é freqüentemente chamado de "velocidade da luz". E existem campos relativísticos da classe 1 que satisfazem a equação

$$

$$Classe 1: \; D ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - (2 \ pi \ mu) ^ 2 (Z - Z_0)$$

Veremos seus exemplos no próximo artigo. Observe que a relatividade não impõe restrições a µ (exceto pela necessidade de µ ² ser positivo) ou a Z ₀ . Para campos relativísticos, existem equações mais complexas, mas a maioria delas na descrição de processos físicos simples é reduzida a um desses dois.

Os campos relativísticos são fisicamente reais e têm um significado físico no Universo, ou seja:

• Suas ondas transportam energia e informações de um lugar para outro.
• Ondas em um campo podem afetar outro campo e alterar os processos físicos que ocorreriam em sua ausência.

Mas, diferentemente dos campos, exemplos dos quais são dados neste artigo, os campos relativísticos não descrevem a propriedade de qualquer meio físico comum, consistindo em qualquer coisa semelhante à matéria comum e, tanto quanto é conhecido experimentalmente, eles não descrevem as propriedades de nada. não importa o que. Esses campos, talvez, até onde sabemos hoje, são um dos elementos fundamentais do Universo.