Entendemos a física de partículas: 7) partículas são quanta

1. Bola em uma mola, versão newtoniana
2. Uma bola quântica em uma mola
3. Ondas, visual clássico
4. Ondas, a equação clássica do movimento
5. Ondas quânticas
6. Campos
7. Partículas são quanta
8. Como as partículas interagem com os campos

Então, finalmente, chegamos ao nosso objetivo: entender o que essas coisas que chamamos de "partículas" são, na verdade, elétrons, fótons, quarks, glúons e neutrinos. Tudo isso, é claro, se aplica à ciência moderna. Vale lembrar que na ciência não há garantias de que o entendimento atual não seja aprofundado.

O artigo anterior descreveu o que são campos - objetos que têm significado em qualquer ponto do espaço e em qualquer momento do tempo (funções do espaço e do tempo), satisfazem a equação do movimento e são fisicamente significativos em termos do fato de serem capazes de transferir energia de um lugar para outro e influenciar os processos físicos do universo.

Aprendemos que a maioria dos campos que conhecemos descreve uma propriedade de um meio, como a altura de uma corda ou a pressão em um gás. Mas também aprendemos que na teoria da relatividade de Einstein há uma classe especial de campos, campos relativísticos que não exigem um meio. Ou pelo menos se eles tiverem um ambiente, é muito incomum. Nada nas equações do campo requer a presença de qualquer meio e não indica qual propriedade desse meio é descrita pelos campos relativísticos.

Portanto, por enquanto, consideraremos os campos relativísticos como objetos físicos elementares do universo, e não como certas propriedades de um meio desconhecido. Se esse ponto de vista será apoiado entre os físicos mais adiante - o tempo dirá.

Consideramos duas classes de campos relativísticos e agora vamos estudá-las com mais detalhes. Eles satisfazem a equação de movimento da Classe 0, onde c _w = c (onde c é o limite de velocidade universal, geralmente chamado de "velocidade da luz").

$$

Ou equações de movimento de classe 1, em que cw = c

$$

No artigo anterior, foi mostrado que μ é a frequência mínima de onda nesses campos. Neste artigo, o denotaremos por ν _min .

Por que o limite de velocidade universal costuma ser chamado de velocidade da luz? Ondas com uma equação da classe 0 se movem com a velocidade c _w . A luz (um termo geral que denota ondas eletromagnéticas de qualquer frequência) movendo-se através do espaço vazio satisfaz a equação relativística da classe 0; portanto, as ondas de luz (e as ondas de quaisquer campos relativísticos que satisfazem a equação relativística da classe 0) se movem com a velocidade c.

Além disso, no mesmo artigo, vimos que, se um campo da classe 1 tem uma onda com amplitude A, frequência ν, comprimento de onda λ e estado de equilíbrio Z ₀ , a equação do movimento exige que a frequência e o comprimento de onda estejam relacionados a μ = ν _min aparecendo nas equações pela fórmula

$$

$$\ nu ^ 2 = (c / \ lambda) ^ 2 + \ mu ^ 2 = (c / \ lambda) ^ 2 + \ nu_ {min} ^ 2$$

Esta é uma fórmula pitagórica - pode ser representada, se desejado, na forma de um triângulo, como na Fig. 1. A frequência mínima de qualquer onda é ν _min e a atribuição ν = ν _min (e, portanto, como λ → ∞) corresponde à compressão do triângulo em uma linha vertical (Fig. 1, abaixo). Você também pode obter um relacionamento semelhante da classe 0 criando μ = ν _min zero. Então você pode extrair a raiz quadrada e obter

$$

$$\ nu = c / \ lambda$$

Este é um triângulo compactado em uma linha horizontal (Fig. 1, à direita). Nesse caso, a frequência mínima é zero. O campo pode flutuar arbitrariamente lentamente.


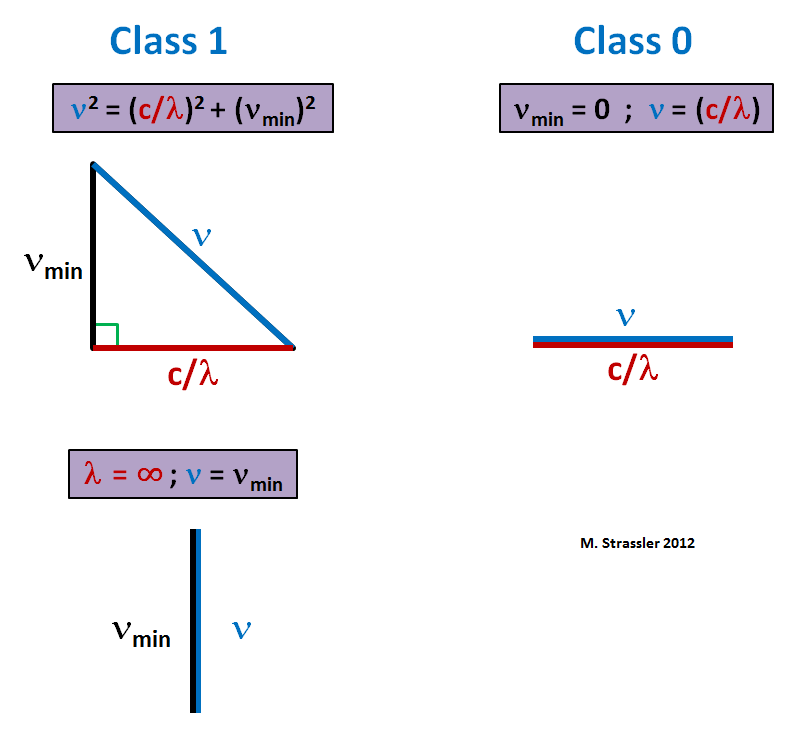Fig. 1

Não há restrições para A. Mas isso é porque estamos ignorando a mecânica quântica. Chegou a hora de estudar os campos quânticos relativísticos.

Campos quânticos relativísticos

O mundo real é mecânico-quântico, então a amplitude A não pode ser nenhuma. São necessários valores discretos proporcionais à raiz quadrada de n, um número inteiro não negativo que indica o número de quanta de vibração na onda. A energia armazenada na onda é

$$

$$E = (n + 1/2) h \ nu$$

Onde h é a constante de Planck, necessariamente aparecendo onde a mecânica quântica é importante. Em outras palavras, a energia associada a cada quantum de oscilações depende apenas da frequência das oscilações da onda e é igual a

$$

$$E = h \ nu$$

Essa relação foi proposta pela primeira vez, especificamente para ondas de luz, por Einstein em 1905, em sua explicação do efeito fotoelétrico.

Mas vamos relembrar nossa razão pitagórica de frequência e comprimento de onda. Se multiplicarmos por h ² , obtemos isso para um campo quântico da classe 1

$$

$$E ^ 2 = (h \ nu) ^ 2 = (h c / \ lambda) ^ 2 + (h \ nu_ {min}) ^ 2 \ quad (*)$$

Parece familiar. Já sabemos que qualquer objeto da teoria da relatividade de Einstein deve satisfazer a equação que descreve sua energia, momento e massa:

$$

$$E ^ 2 = (pc) ^ 2 + (mc ^ 2) ^ 2$$

Outra relação pitagórica. A energia mínima do objeto é mc ² , que se assemelha à afirmação sobre a frequência mínima que uma onda da classe 1, ν _min , pode possuir. Podemos ficar tentados a supor que, provavelmente, para um quantum de um campo relativístico

$$

$$p c = h c / \ lambda \ quad (**)$$

$$

$$m c ^ 2 = h \ nu_ {min} \ quad (***)$$

A primeira equação apareceu pela primeira vez na obra de Louis De Broglie em 1924 - quase 20 anos depois de Einstein. Por que demorou tanto tempo? Eu não sei


Fig. 2

Isso faz sentido? Como observamos, os campos relativísticos de classe 0 também incluem campos elétricos e suas ondas são ondas eletromagnéticas, ou seja, luz. A versão da fórmula (*) que obtemos para os quanta da classe 0 é a mesma dos campos da classe 1 para os quais μ = ν _{min é} igual a zero - ou seja, m = 0. Extraímos a raiz quadrada e obtemos

$$

$$E = p c$$

Ou a equação de Einstein para partículas sem massa. E os quanta das ondas eletromagnéticas (incluindo todos os tipos de luz: visível, ultravioleta, infravermelho, ondas de rádio, radiação gama, etc., diferindo apenas em frequência e, portanto, a energia dos quanta) serão realmente partículas sem massa - assim que aplicarmos o indicado acima de algumas equações (**) e (***). Estes são fótons.

A partir da equação (***), podemos finalmente calcular a massa da partícula. Cada partícula que tem uma massa é um quantum de um campo da classe 1. A frequência mínima de tais ondas é ν _min . A energia mínima de um quantum dessa onda é igual a h vezes a frequência. E a massa da partícula é simplesmente a energia mínima dividida por c ² .

$$

$$m = h \ nu_ {min} / c ^ 2$$

Se queremos entender de onde vem a massa de partículas, precisamos entender o que determina v _min e por que há uma frequência mínima em geral. Para partículas como elétrons e quarks, isso não é totalmente claro, mas sabe-se que o campo de Higgs desempenha um papel importante nisso.

Concluímos: partículas da natureza são quanta de campos quânticos relativísticos. Partículas sem massa são quanta de ondas de campo que satisfazem uma equação da classe 0. As que possuem massa correspondem aos campos de uma equação da classe 1. Existem muitos detalhes, mas esse fato é uma das propriedades fundamentais do nosso mundo.

Esses quanta realmente se comportam como partículas?

Imaginamos partículas como partículas de poeira ou grãos de areia. Nesse sentido, os quanta não são partículas - são ondas que têm uma energia e amplitude mínimas para uma determinada frequência. Mas eles se comportam tanto como partículas que podemos ser perdoados por usar a palavra "partícula" em sua descrição. Vamos ver o porquê.

Se você pegar uma onda na água e deixá-la passar por pedras rasas abaixo da superfície, parte da onda cruzará a linha de pedras e parte será refletida, conforme mostrado na Fig. 3. Qual parte da onda cruzará a linha depende da forma das pedras, da proximidade da superfície, etc. Mas o ponto principal é que parte da onda é transmitida através das pedras e parte será refletida. Parte da energia das ondas irá na mesma direção, parte irá na direção oposta.


Fig. 3

Mas se você enviar um fóton em direção ao vidro reflexivo, esse fóton passará por ele ou será refletido (Fig. 4). Mais precisamente, se você medir o comportamento de um fóton, descobrirá se ele é refletido ou transmitido. Se você não medir, será impossível dizer o que aconteceu. Bem-vindo ao pântano da mecânica quântica. Um fóton é um quantum. Sua energia não pode ser dividida na parte que passou pelo vidro e na parte que foi refletida - porque, em cada lado, haverá menos de um quantum, o que é proibido. (Letras pequenas: o vidro não altera a frequência dos fótons, portanto a energia não pode ser dividida entre dois ou mais quanta de frequências mais baixas). Portanto, o fóton, embora seja uma onda, se comporta como uma partícula neste caso. Ou reflete fora do vidro ou não. Seja refletida ou não, a mecânica quântica não prevê isso. Dá apenas a probabilidade de reflexão. Mas ela prevê que, aconteça o que acontecer, o fóton viajará como uma unidade e manterá sua identidade.


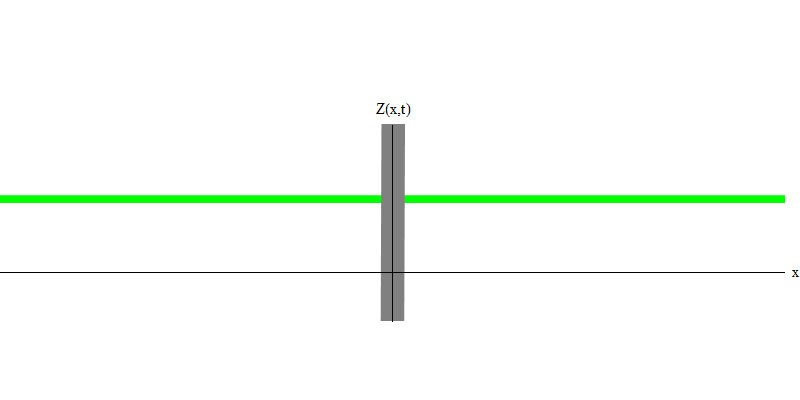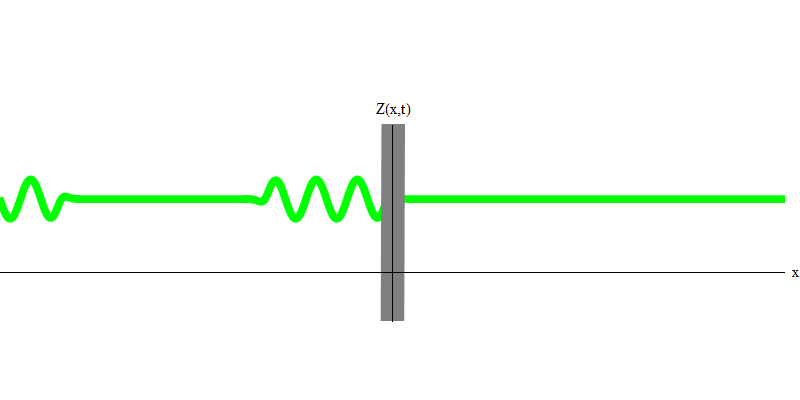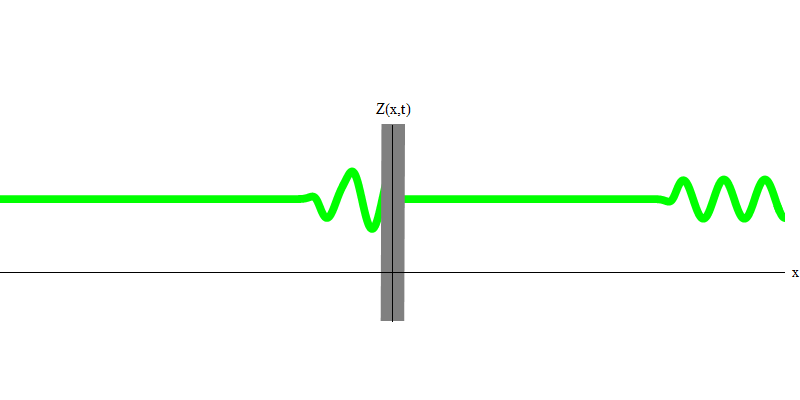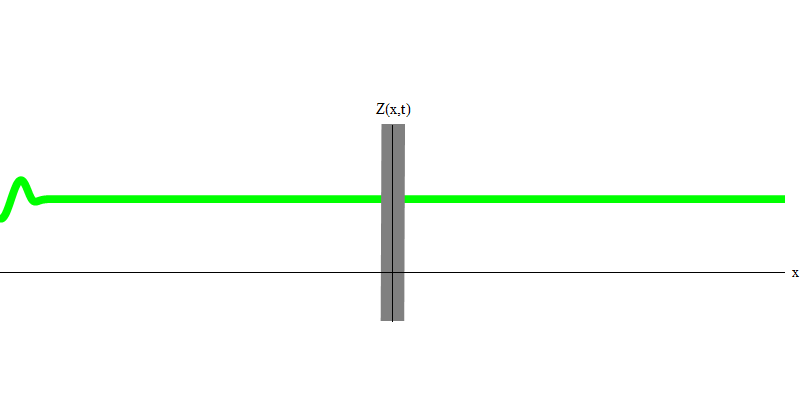Fig. 4

E o que acontecerá com os dois fótons? Isso depende Por exemplo, se os fótons são emitidos em momentos diferentes de lugares diferentes, o observador verá dois quanta, separados no espaço, e provavelmente se movendo em direções diferentes (Fig. 5). Eles podem ter frequências diferentes.


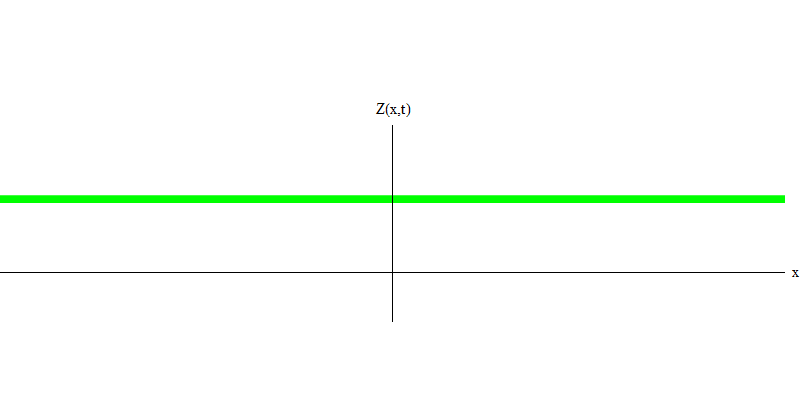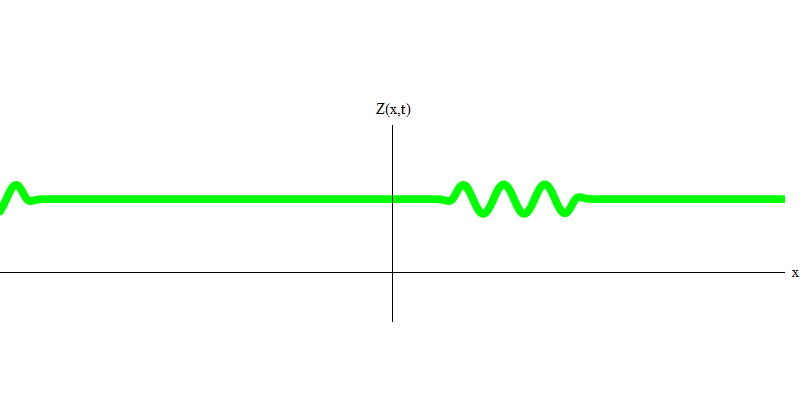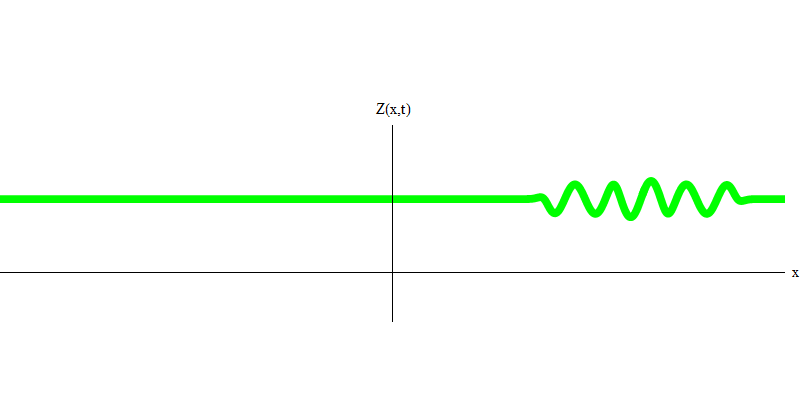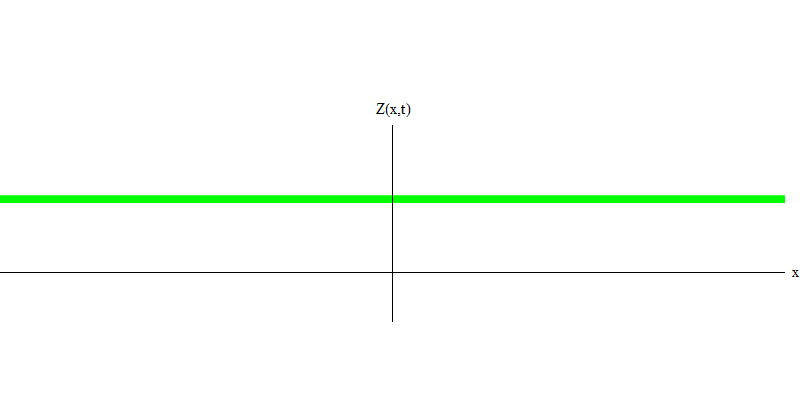Fig. 5: quanta independente

No caso especial, quando dois fótons são emitidos juntos e perfeitamente sincronizados (como nos lasers), eles se comportam como mostrado na Fig. 6. Se enviarmos uma combinação de dois fótons para o vidro, não dois, mas três coisas podem acontecer. Ambos os fótons passarão pelo vidro, ou ambos serão refletidos, ou um passará e o outro será refletido. 0, 1 ou 2 fótons serão refletidos no vidro - não há outras opções. Nesse sentido, os quanta leves novamente se comportam como partículas, como pequenas bolas - se você atirar duas bolas em uma grade com furos, então 0, 1 ou 2 bolas serão refletidas na grade e 0, 1 ou 2 bolas passarão pelos furos . Não há possibilidade de que 1.538 objetivos sejam refletidos na rede.


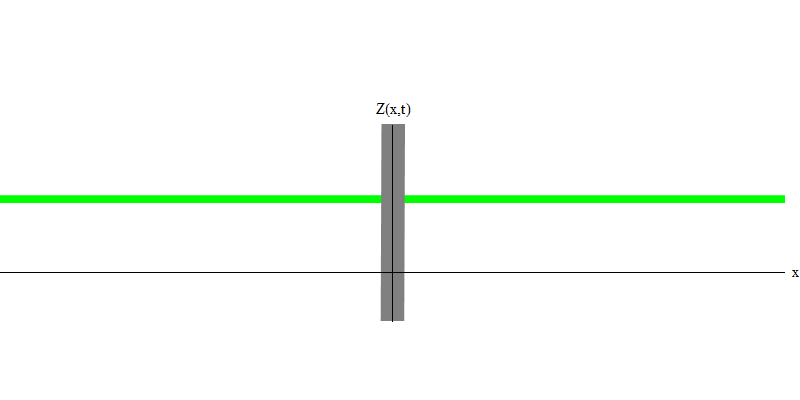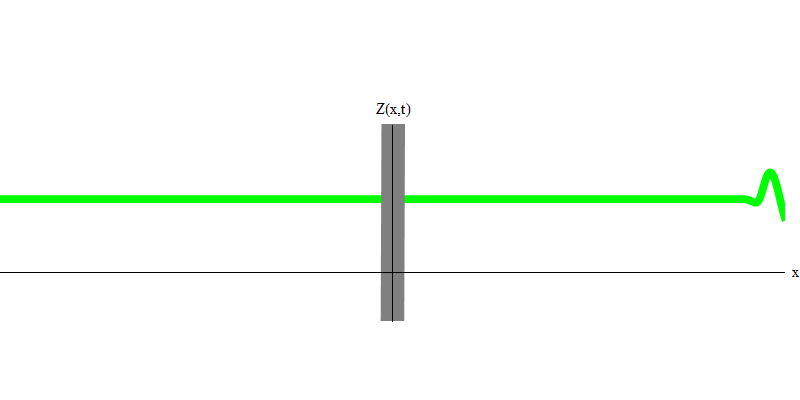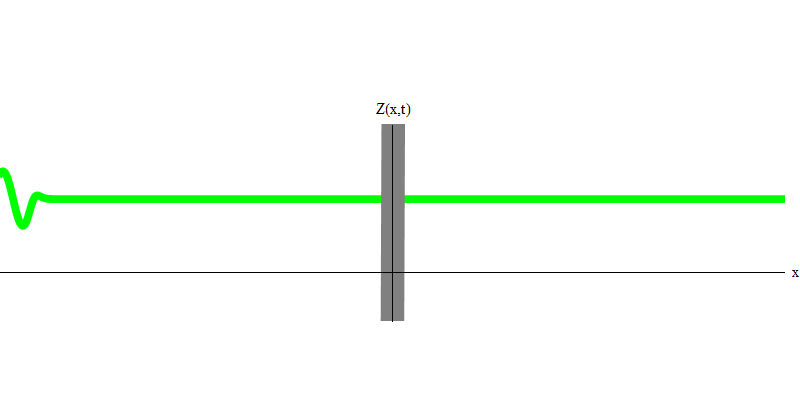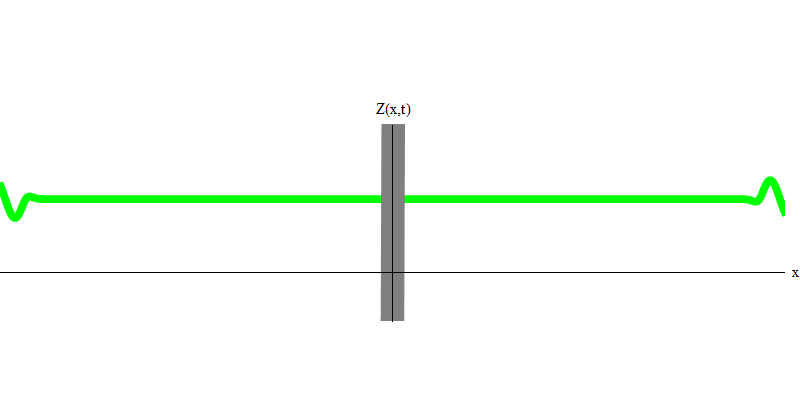Fig. 6

Mas estes são fótons que, sem massa, são obrigados a se mover na velocidade da luz e E = p c. E quanto a partículas com massa como elétrons? Os elétrons são quanta do campo elétrico e, como os fótons, podem ser emitidos, absorvidos, refletidos ou transmitidos como um todo. Eles têm certa energia e impulso, $$$E ^ 2 = (pc) ^ 2 + (m_e c ^ 2) ^ 2$onde m _e é a massa do elétron. A diferença entre elétrons e fótons é que eles se movem mais lentamente que a luz e, portanto, podem descansar. O esboço de um evento desse tipo (na mecânica quântica, devido ao princípio da incerteza, nada pode ser verdadeiramente estático) de um elétron estacionário é apresentado na Fig. 7. Essa é uma onda de frequência mínima obtida pela atribuição de um comprimento de onda de um valor muito grande, quase infinito. Portanto, a forma de onda espacial na Fig. não mostra nenhuma complicação - apenas flutua no tempo.


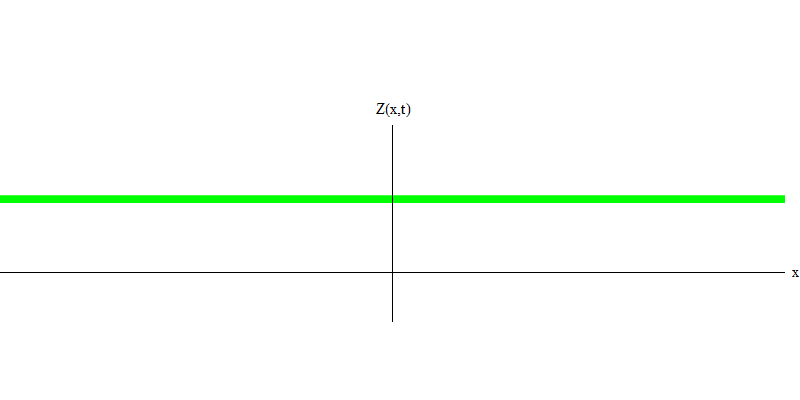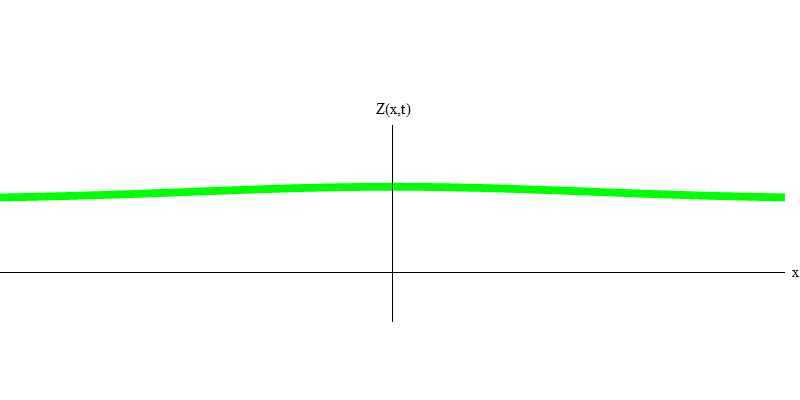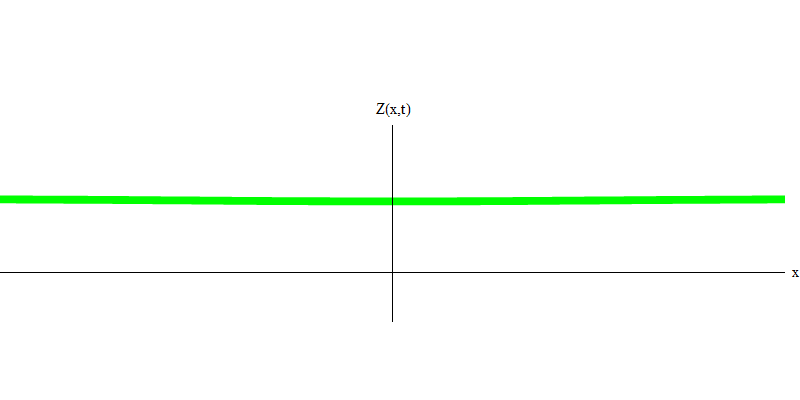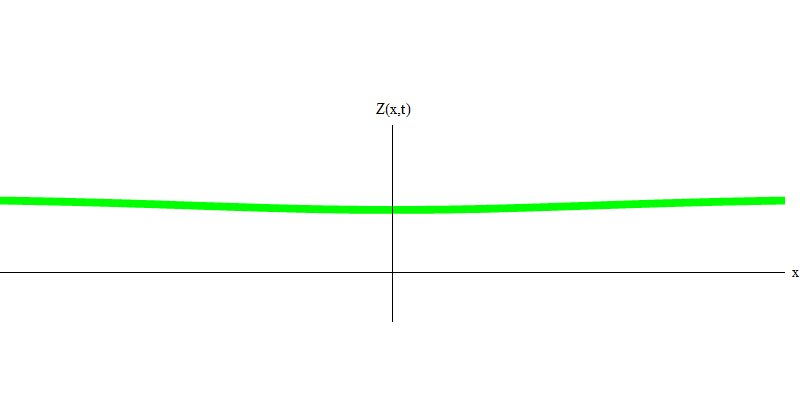Fig. 7

Então, sim, de fato, os quanta se comportam muito como partículas e, portanto, chamar elétrons, quarks, neutrinos, fótons, glúons, partículas W e partículas de Higgs de "partículas" não será um engano catastrófico. Mas a palavra "quantum" é mais adequada para isso - porque esses são precisamente quanta.

Como os férmions e os bósons diferem um do outro?

• Todas as partículas elementares são divididas em férmions e bósons.
• Os férmions (incluindo elétrons, quarks e neutrinos) atendem ao princípio de exclusão de Pauli - dois férmions do mesmo tipo não podem fazer a mesma coisa.
• Os bósons (incluindo fótons, partículas W e Z, glúons, gravitons e partículas de Higgs) são diferentes: dois ou mais bósons do mesmo tipo podem fazer a mesma coisa.

É por isso que os lasers podem ser feitos de fótons - já que são bósons, eles podem estar no mesmo estado e gerar um poderoso raio de uma luz. Mas um laser não pode ser feito de elétrons que são férmions.

Como essa diferença se manifesta na linguagem da matemática? Acontece que as fórmulas que trago são adequadas para bósons e para férmions elas precisam ser alteradas - um pouco, mas com grandes consequências. Para bósons teremos:

$$

$$E = (n + 1/2) h \ nu, \ quad onde \; n = 0, 1, 2, 3, 4, ...$$

O que significa que a energia de cada quantum é igual a h ν. Isso implica que os bosques quanta podem fazer a mesma coisa; quando n for maior que 1, a onda no campo bosônico consistirá em vários quanta oscilando e se movendo juntos. Mas para férmions:

$$

$$E = (n - 1/2) h \ nu, \ quad onde \; n = 0 \; ou \; 1$$

A energia de um quantum ainda é igual a h ν, de modo que toda a discussão sobre partículas e suas energias, momento e massas permanece válida. Mas o número de quanta em uma onda de elétrons pode ser de apenas 0 ou 1. Dez elétrons, ao contrário de dez fótons, não podem ser organizados em uma onda de maior amplitude. Portanto, não há ondas de férmion que consistem em um grande número de férmions, oscilando e se movendo juntos.