
A teoria das cordas é freqüentemente chamada de "teoria de tudo" porque seu objetivo é descrever todas as forças fundamentais da interação no universo, incluindo a gravidade, a mecânica quântica e a teoria da relatividade. Esse conceito revolucionário introduz uma nova compreensão do espaço e do tempo; procura explicar a conexão entre fenômenos como buracos negros e plasma de quarks e glúons, dimensões adicionais e flutuações quânticas.
Apesar da complexidade do tópico em consideração, o professor da Universidade de Princeton, Stephen Gabser, oferece uma introdução ampla, acessível e divertida a essa das áreas mais discutidas da física atualmente. Com um mínimo de matemática, usando analogias interessantes, o autor explica a essência da supersimetria, dualidade, curvatura do espaço-tempo, para que fique claro para qualquer leitor que possua conhecimentos sobre o ensino médio.
Embora as disposições da teoria das cordas não tenham sido conclusivamente comprovadas, no entanto, esses segredos que já nos foram revelados nos permitem admirar a harmonia harmoniosa do universo e discutir a aplicação prática de futuras descobertas na física de alta energia.
Gravidade versus mecânica quântica
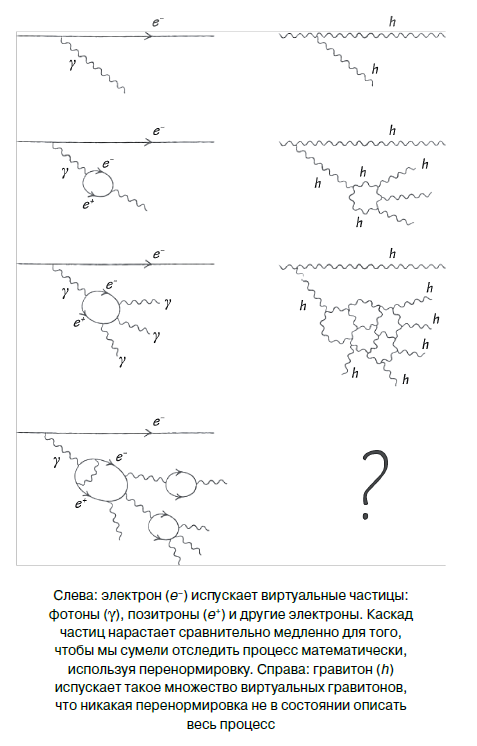
A mecânica quântica e a relatividade geral - as duas teorias físicas triunfais que surgiram no início do século XX - mostraram-se inconsistentes entre si. A dificuldade surge ao aplicar o método chamado renormalização. Vou falar sobre renormalização usando o exemplo de fótons e gravitons, sobre os quais já falamos nos capítulos anteriores. A essência da inconsistência é que os fótons nos levam a uma teoria renormalizável (que significa: "boa teoria"), enquanto os gravitons levam a uma teoria não-normalizável, e isso realmente significa que não temos uma teoria geral que descreva fótons e gravitons.
Os fótons interagem com as cargas elétricas, mas são eletricamente neutros. Por exemplo, um elétron com carga elétrica em um átomo de hidrogênio, saltando de um nível de energia para outro, emite um fóton. É exatamente isso que quero dizer quando digo que os fótons interagem com as cargas. A afirmação de que o fóton em si não possui carga elétrica é equivalente à afirmação de que a luz não conduz eletricidade. Se não fosse assim, você receberia um choque elétrico toda vez, agarrando-se a um objeto que ficava exposto à luz do sol por um tempo suficiente. Os fótons não interagem entre si; eles interagem apenas com cargas elétricas.
Os gravitons não respondem a cargas, mas a massa, energia e momento. E uma vez que transferem energia, eles também interagem entre si. Pode parecer que isso não apresenta um problema específico, mas é justamente por isso que encontramos dificuldades. A mecânica quântica nos ensina que os gravitons se comportam como ondas e como partículas. Partículas são objetos pontualmente hipotéticos. E o ponto graviton irá atraí-lo quanto mais forte, mais perto você se aproxima dele. Seu campo gravitacional pode ser descrito como a emissão de outros gravitons. Vamos chamar o julgamento de graviton materno, e os gravitons emitidos por ele - filha. O campo gravitacional próximo ao graviton mãe é muito forte. Então, os gravitons de sua filha têm enormes energias e momentos. Isso segue diretamente o princípio da incerteza: os gravitons filhas são observados a uma distância muito pequena Δx do gravitão-pai e, portanto, de acordo com a relação de incerteza, Δp × Δx ≥ h / 4π, sua incerteza de momento, Δp, é muito grande. O problema é que os gravitons também são sensíveis ao momento. Os próprios gravitons da filha emitirão gravitons. Todo o processo se ramifica e diverge incrivelmente rápido: você não pode levar em consideração todas as conseqüências da interação de todos os gravitons.
De fato, algo semelhante acontece perto do elétron. Se você tentar medir o campo elétrico muito próximo ao elétron, faça com que ele emita um fóton com um momento muito grande. Isso parece inofensivo porque, como sabemos, os fótons não emitem outros fótons. O problema é que um fóton pode dar à luz um par elétron-pósitron, que emite ainda mais fótons que geram novos elétrons e pósitrons ... Uma bagunça completa! O mais surpreendente é que, no caso de elétrons e fótons, você pode, no entanto, descrever completamente toda a multidão de partículas em cascata uma da outra. Às vezes, eles falam sobre roupas, ou "casacos de pele", da prole na qual um elétron é enrolado. Os físicos usam o termo "partículas virtuais" para descrever a progênie eletrônica. A renormalização é um método matemático que permite rastrear toda essa bagunça.
A idéia da renormalização é que se supõe que um elétron "vazio" tenha carga infinita e massa infinita, mas assim que "vestimos" um elétron, sua carga e massa adquirem valores finitos.
O problema com os gravitons é que não somos capazes de renormalizar a nuvem de gravitons virtuais ao seu redor. A teoria geral da relatividade - a teoria da gravidade - é não-renormalizável. Isso pode parecer um problema técnico confuso: há poucas chances de estarmos simplesmente olhando para o problema do lado errado. Há também uma chance ainda mais fraca de que uma teoria chamada Teoria da Supergravidade Máxima seja renormalizável. No entanto, eu e a maioria dos teóricos das cordas estamos convencidos de que existem dificuldades fundamentais na combinação da mecânica quântica e da gravidade.
Agora vamos dar uma teoria das cordas. A suposição inicial subjacente é que as partículas não são partículas pontuais. Em vez disso, as partículas são representadas como modos vibracionais de uma corda. De acordo com a idéia geralmente aceita da teoria das cordas, as cordas são objetos infinitamente finos, mas com um comprimento finito (da ordem de 10 a 34 metros), interagindo entre si à maneira dos gravitons. Pare, pare! - você protesta. "Mas, neste caso, os problemas gerais com a nuvem de partículas virtuais - nesse caso, cadeias virtuais - não nos levarão à mesma impossibilidade de rastrear todo o processo de interação, como no caso dos gravitons?" Não. O fato de as strings não serem objetos de ponto mata o problema descrito pela raiz. A fonte de dificuldade no caso dos gravitons é a suposição de que eles, de acordo com o termo “partícula pontual”, são infinitamente pequenos. Substituir gravitons por cordas vibrantes suaviza os "ângulos agudos" de sua interação. “Nos dedos”, isso pode ser explicado da seguinte forma: quando o gravitô dá origem a outro gravitó virtual, é possível indicar com precisão o local e a hora em que isso aconteceu. Mas quando a corda se ramifica, parece um galho de um cano de água.
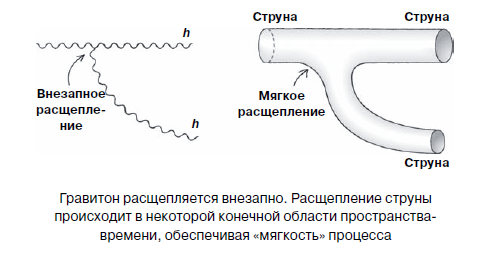
No ponto de ramificação, não há um ponto em que ocorra uma ruptura, a figura em forma de Y que ilustra esse processo se parece com um segmento de tubo contínuo e suave, apenas com uma forma incomum. Tudo isso leva ao fato de que a divisão da corda é um processo mais "suave" do que a divisão da partícula. Os físicos dizem que as cordas interagem com a natureza "suavemente", enquanto as partículas interagem com a natureza "com força". É essa suavidade que fornece o melhor comportamento da teoria das cordas do que a teoria geral da relatividade, em relação à aplicabilidade da descrição da mecânica quântica.
Strings no espaço-tempo
Lembre-se brevemente do que estávamos falando sobre as vibrações da corda do piano. Se você apertar a corda com força entre dois pinos e bater com um martelo, ela vibrará com uma certa frequência. Frequência é o número de oscilações por segundo. Além da frequência principal, a corda do piano também vibra com sobretons, que são vibrações de frequências mais altas que dão ao som do piano uma cor característica. Eu citei essa analogia ao descrever o comportamento de um elétron em um átomo de hidrogênio: ele também possui um modo vibracional fundamental correspondente ao estado fundamental com energia mínima e modos adicionais correspondentes a níveis mais altos de energia.
A analogia descrita pode não satisfazê-lo completamente: "Bem, o que o elétron no átomo de hidrogênio tem a ver com a onda estacionária na corda do piano?" - você pergunta. A maioria está mais próxima da analogia com o planetóide infinitamente pequeno circulando em órbita ao redor do minúsculo sol - o núcleo atômico, não é? Essa analogia é boa? Sim e não A mecânica quântica afirma que a idéia de um elétron como partícula e a idéia de um elétron como uma onda estão tão entrelaçadas que o movimento mecânico-quântico de uma partícula de elétron em torno de um próton pode realmente ser descrito como uma onda estacionária.
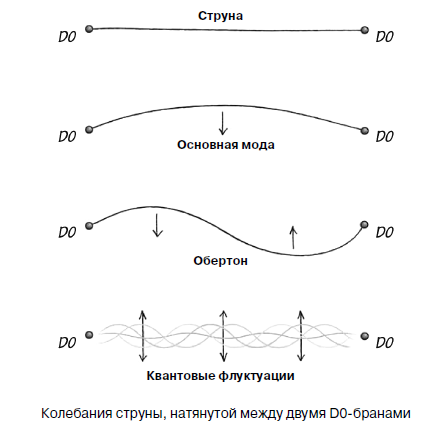
Comparar uma corda de piano com as que aparecem na teoria das cordas é realmente um método muito correto. Para evitar confusão com diferentes tipos de cadeias, chamarei aquelas que a teoria das cordas lida com "cadeias relativísticas". Este termo tem um significado didático muito profundo, porque a teoria das cordas inclui a teoria da relatividade, tanto especial quanto geral. Agora, quero falar sobre uma construção da teoria das cordas que é tão parecida com uma corda de piano quanto uma corda pode até ser como uma corda. Cordas relativísticas podem terminar em objetos chamados D-branas. Se omitirmos os efeitos associados à interação de cadeias, as D-branas podem ser consideradas infinitamente pesadas. Detalhes sobre as farinhas D serão discutidos no próximo capítulo, e agora farei apenas uma pequena digressão, por assim dizer, como uma "muleta". A D-brana mais simples é chamada de D0-brana (pronunciada “de-zero brane”). Esta é uma partícula pontual. Já posso ouvir a indignação de alguns leitores sobre o retorno às partículas pontuais: "O autor não afirmou recentemente que a teoria das cordas visa se livrar das partículas pontuais?" Bem, sim, isso foi até meados dos anos 90, e as partículas pontuais voltaram novamente à teoria das cordas, e não sozinhas, mas levaram a um zoológico inteiro de animais desconhecidos. Mas estou me adiantando. Tudo o que quero fazer é fornecer o análogo teórico das cordas dos pinos de piano que mantêm a corda em um estado tenso - e as branas D0 são tão apropriadas nesse papel que não consigo resistir a contar sobre elas. Em resumo, puxamos a corda relativista entre duas branas D0, como uma corda de piano entre duas cavilhas. As próprias D0-branas não estão ligadas a nada, mas permanecem imóveis porque possuem massa infinita. Engraçado, não é? Então tudo bem. Sobre D0-branas - no próximo capítulo e agora - apenas sobre uma corda esticada.
O nível mais baixo de energia de uma corda esticada corresponde à ausência de vibrações. Bem ... quase ausente, porque pequenas oscilações quânticas estão sempre presentes, e esse fato é importante. É mais correto imaginar o nível mais baixo de energia como tendo uma pequena energia vibracional dentro da estrutura do que é permitido pela mecânica quântica. Os níveis excitados de uma corda relativística correspondem às suas oscilações na frequência fundamental ou nas conotações da frequência fundamental, e também podem vibrar em várias frequências simultaneamente, como uma corda de piano. Mas, assim como um elétron em um átomo de hidrogênio, uma corda relativista não pode vibrar em uma frequência arbitrária. Um elétron pode selecionar níveis de energia de um conjunto discreto. Cordas relativísticas são exatamente as mesmas. Diferentes níveis vibracionais têm energias diferentes e, como massa e energia estão relacionadas pela relação E = mc2, diferentes massas correspondem a diferentes estados vibracionais.
Seria ótimo se eu pudesse dizer que a frequência de vibração de uma corda está relacionada à sua energia por uma simples relação do tipo E = hν, como foi o caso dos fótons. Infelizmente, isso não é tão simples. A massa total da corda é composta por vários componentes. A primeira delas é a massa restante da corda, que corresponde à energia de tensão da corda entre duas D0-branas. A segunda é a massa correspondente à energia vibracional, que por sua vez consiste nas energias vibracionais de todas as conotações. Lembre-se de que energia e massa estão relacionadas pela relação E = mc2. E finalmente, o terceiro componente é a massa correspondente à energia de flutuações quânticas irrecuperáveis, chamadas oscilações de ponto zero. O termo "vibrações zero" nos faz lembrar da inevitabilidade fundamental das flutuações quânticas. Então: a contribuição da energia do ponto zero para a massa da corda ... é negativa! Eu concordo, isso é estranho. Muito estranho Para mostrar como isso é estranho, darei um exemplo. Se nos restringirmos a um único modo vibracional de uma corda, veremos que a energia das vibrações de ponto zero desse modo é positiva. Cada uma das conotações mais altas individualmente dá uma contribuição positiva ainda maior à energia da corda. Mas se somarmos adequadamente as contribuições de todas as conotações, obteremos um número negativo. Se você acha que isso não é ruim o suficiente, então isso é uma notícia ainda mais ruim: ocultei parte da verdade dizendo que a contribuição da energia das vibrações do ponto zero é negativa. Todos esses efeitos - massa de repouso, energia vibracional e energia vibracional de ponto zero - entram na expressão da massa total pelos quadrados de seus valores. E se a energia das vibrações do ponto zero prevalecer nessa soma, então o quadrado da massa total é negativo, o que significa que a própria massa é imaginária, como a raiz de menos uma.
Antes de você rejeitar indignadamente esse absurdo, deixe-me acrescentar que, na teoria das cordas, toda uma linha de pesquisa é dedicada à eliminação do problema descrito. Em poucas palavras, o problema é que o quadrado da massa da corda relativística em seu estado de energia mais baixo é negativo. As cordas nesse estado são chamadas de taquiões. Sim, sim, esses são os mesmos táquions que em cada série confrontam os heróis de Star Trek. Esta é definitivamente uma má notícia. No modelo que descrevi, seria possível livrar-se do quadrado negativo da massa puxando as branas D0 às quais as extremidades da corda estão presas, longe o suficiente para que a energia de tensão da corda se torne maior que a energia de vibração do ponto zero. Mas quando não há D0-branes por perto, a própria cadeia ainda permanece. Privado da capacidade de se apegar a algo, ele pode se tornar fechado. Agora ela não está esticada entre algo e algo e pode flutuar, mas talvez não. A única coisa que ela não pode parar de fazer é flutuar no nível quântico. E, como antes, as oscilações quânticas transformam essa corda em um táquion, o que é muito, muito ruim para a teoria. De acordo com conceitos modernos, os táquions são instáveis, são semelhantes a um lápis que se equilibra na ponta. Você pode tentar equilibrar esse lápis, mas qualquer respiração leve o derrubará. A teoria das cordas contendo taquiões lembra uma teoria que descreve milhões de lápis em pé no espaço de preenchimento das bordas.
No entanto, eu exagerei demais. Existe uma solução econômica para os táquions. Suponha que o estado fundamental de uma corda de táquion corresponda à massa imaginária e ao seu quadrado: m2 <0. A energia vibracional também dá uma certa contribuição ao quadrado da massa. Usando o baralho correto e entregando as cartas da maneira necessária, você pode garantir que a massa total da corda seja exatamente zero. Isso é encorajador porque, como sabemos, no mundo real existem partículas sem massa, como fótons ou gravitons. Portanto, se as strings realmente descrevem o mundo real, elas devem ser sem massa ou, mais estritamente, pelo menos alguns dos estados quânticos das strings devem ser sem massa.
Observe que você precisa pegar o baralho correto. Com essa metáfora, eu queria dizer que precisamos do espaço-tempo 26-dimensional. Você já deve ter adivinhado que tudo chegará a essa desgraça, então não vou me desculpar. Existem vários argumentos a favor de 26 dimensões, mas a maioria é puramente matemática, e tenho medo de que não pareçam convincentes para a maioria dos leitores. O argumento que darei é mais físico. Gostaríamos de obter estados quânticos sem massa de strings. Sabemos que as oscilações do zero quântico “empurram” m2 na direção negativa. Também sabemos que os modos vibratórios "empurram" m2 na direção oposta. O valor mínimo possível da energia vibracional não depende da dimensão do espaço, enquanto a magnitude das vibrações quânticas nulas depende. Vejamos deste lado: quando algo hesita - uma corda de piano ou outra coisa - ele o faz em uma determinada direção. A corda do piano oscila na direção em que o martelo o atingiu; por exemplo, uma corda de piano oscila para cima e para baixo, mas não para a direita ou para a esquerda. A oscilação seleciona uma direção e ignora o resto. Em contraste, as vibrações do ponto zero da mecânica quântica ocorrem em todas as direções possíveis, e a adição de cada nova dimensão adiciona flutuações quânticas em outra direção na qual as oscilações podem ocorrer. Direções mais possíveis de oscilações, ou, como são chamadas, graus de liberdade, significa um número maior de flutuações, o que leva a uma maior contribuição negativa para m2. Resta apenas calcular como escolher as contribuições para a massa total de modos vibracionais e vibrações zero. Acontece que um modo oscilatório com um valor mínimo de energia é compensado por uma oscilação quântica zero de 26 dimensões. Veja isso com otimismo, porque o número de medições necessárias pode ser não integral! O que faríamos, por exemplo, com 26 dimensões e meia?
Se você não dominar completamente os diferentes tipos de flutuações, não se preocupe. Eles são muito parecidos. A única diferença entre os modos vibracionais e as vibrações quânticas zero é que os modos vibracionais podem ou não estar presentes, enquanto as vibrações zero estão sempre presentes. Vibrações zero são aqueles movimentos mínimos, cuja presença é exigida pelo princípio da incerteza. Além do modo principal, sobretons estão presentes nas vibrações da corda, dando à corda novas propriedades quântico-mecânicas. Prefiro imaginar vários modos na forma de modelos mecânicos simples, como vibrações circulares, vibrações na forma de uma folha de trevo ou vibrações torcionais. . , . , , -. , . — - .
, : , . , , . . 26- . . , , , . .
, 26 10. , . - . --, , . . -- , « », . , , - ˆ, ˆ. , . - . — . - , .
, . . -, . , , , , . , , , , , , - , , , , . , . , - , , . . . , . — .
»Mais informações sobre o livro podem ser encontradas no
site do editor»
Conteúdo»
Trecho20% —