Entendemos a física de partículas: 8) como as partículas interagem com os campos

Entendendo a física de partículas:
1. Bola em uma mola, versão newtoniana
2. Uma bola quântica em uma mola
3. Ondas, visual clássico
4. Ondas, a equação clássica do movimento
5. Ondas quânticas
6. Campos
7. Partículas são quanta
8. Como as partículas interagem com os campos

Como o campo Higgs funciona:
1. A ideia principal

Em um artigo anterior da série, expliquei que as partículas da natureza são quanta de campos relativísticos que satisfazem as equações de movimento da classe 0 e da classe 1. Mas o que eu não disse até agora, então essa afirmação, felizmente, é apenas parcialmente verdadeira. As equações reais são sempre um pouco mais complicadas, de modo que a interconexão de partículas e campos permanece, mas fenômenos e processos muito mais diversos se tornam possíveis, incluindo o aparecimento de partículas após a colisão de outras partículas, o decaimento de partículas em outras partículas e a dispersão de partículas entre si, bem como a formação de objetos interessantes como prótons e nêutrons, núcleos atômicos e átomos. Não poderei explicar tudo isso em detalhes, mas neste artigo apresentarei uma introdução de como tudo funciona.

A principal diferença entre as equações, que chamei de "classe 0" e "classe 1", e as equações significativas para a física real, é que nas equações reais existem termos adicionais que dependem de dois ou mais campos, e não apenas um . Ou seja, digamos, em vez de uma equação da classe 0 para um campo relativístico Z (x, t), que se parece com

$$

para campos reais, as equações se parecem mais com isso:

$$

Onde y e y 'são números (geralmente menores que 1), Z é uma notação curta de Z (x, t) e A (x, t) e B (x, t) são um par de outros campos. Em tais equações, pode-se esperar a aparência de termos como A (x, t) Z (x, t) ou A (x, t) ² Z (x, t) ou Z (x, t) ² ou mesmo A (x, t) d ² Z / dt ² , etc. Quais membros podem e quais não podem aparecer dependem dos detalhes dos campos envolvidos no processo. As regras são rígidas, mas bastante confusas, por isso não as abordaremos por enquanto. Em geral, a partir de experimentos, estabelecemos (e entendemos do ponto de vista teórico) que, na natureza:

• Qualquer termo válido em princípio (conservação da carga elétrica ou correspondência da relatividade de Einstein) aparece nas equações,
• mas membros com muitos campos geralmente são muito pequenos e insignificantes em comparação com membros com um, dois e às vezes três campos (membros com derivadas de tempo ou espaço também são geralmente pequenos).

Portanto, nos processos físicos mais interessantes, é possível focar em todos os termos válidos com um, dois ou três campos.

Um pouco de terminologia. Os termos nas equações com campos são chamados lineares no primeiro grau. Todos os termos em nossas equações de classe 0 ou 1 eram lineares. Membros com dois ou três campos são chamados quadráticos ou cúbicos; em geral, eles são chamados não lineares. Todos os fenômenos interessantes do nosso mundo aparecem devido a termos não lineares nas equações de movimento - a saber, a interação dos campos entre si e com eles mesmos. Vamos estudar um deles.

O surgimento de uma nova onda a partir da ressonância das outras duas

Para ter uma idéia de como tudo pode se tornar interessante, tomamos três campos, A (x, t), B (x, t), C (x, t) e uma situação simplificada. Suponha que os campos A e B satisfaçam aproximadamente as equações da classe 0 (e contenham quanta sem massa), e o campo C satisfaça as equações da classe 1 (contém ondas com uma frequência mínima ν _min e, consequentemente, quanta com massa m = h ν _min / c ² , em que h - constante de Planck). Também adicionaremos termos não lineares às suas equações. Especificamente, assim (por questões de brevidade, escreveremos "A" em vez de "A (x, t)" e assim por diante, c é a velocidade da luz, y é um número que geralmente é menor que 1):

$$

Impressão fina: adicionei termos não lineares às três equações porque a presença de tais termos em uma das equações e a ausência deles na outra levará a contradições; por exemplo, a energia não será conservada. Para o processo que estou descrevendo, precisaremos considerar apenas termos não lineares nas equações de movimento do campo C.

Vamos ver o que acontece com esse conjunto de equações se a onda do campo A encontrar a onda do campo B. Em princípio, podemos adivinhar isso aplicando o método do exame minucioso. Se houver uma onda no campo A, então A (x, t) é diferente de zero perto dele. Quando as ondas dos campos A e B se sobrepõem, o resultado da multiplicação de A (x, t) e B (x, t) torna-se diferente de zero. Agora, passamos à equação para C: alterações no campo C no tempo e no espaço (dois termos no lado esquerdo) estão associadas ao produto A e B (um dos termos no lado direito).

$$

Portanto, mesmo que o campo C seja zero quando A (x, t) B (x, t) se torna diferente de zero, então C (x, t) logo se tornará diferente de zero na mesma seção. Em resumo, como resultado do encontro das ondas A e B, ocorrerá um pequeno distúrbio no campo C.

Letras pequenas: você pode estar interessado - depois que C se torna diferente de zero, se o termo A (x, t) C (x, t) se torna na equação de movimento do campo, causando perturbações adicionais no campo B. A resposta é sim, mas esse efeito será ainda menor. Até ignorá-lo e depois descobrir por que valeu a pena fazer isso.

Na fig. A Figura 1 mostra uma onda com uma frequência ν no campo A (verde), que ocorre com uma onda de frequência ν no campo B (azul). Eu equalizei as frequências por simplicidade e simetria. Mais tarde, veremos por que outros casos se resumem a isso. A velocidade ν pode ser estimada observando a onda verde e a linha vertical localizada em um ponto no espaço e oscilando com a onda.

O produto laranja abaixo mostra o produto A (x, t) B (x, t); pode-se ver que se torna diferente de zero quando duas ondas são sobrepostas. Também é visto que varia no tempo. Você pode ver (comparando-o com uma barra vertical oscilante) que A (x, t) B (x, t) oscila duas vezes mais rápido. Lembre-se deste fato importante. No caso geral, se uma onda de frequência ν ₁ encontrar uma onda de frequência ν ₂ , seu produto irá oscilar com uma frequência ν ₁ + ν ₂ . E mais uma coisa: você pode notar que as vibrações AB não se movem para a direita ou esquerda, elas permanecem no lugar. Mais tarde veremos por que isso é importante.


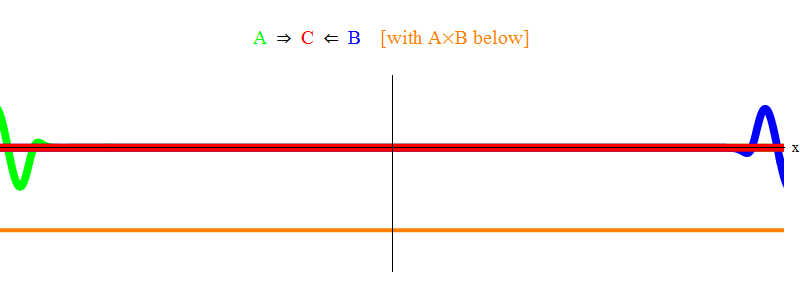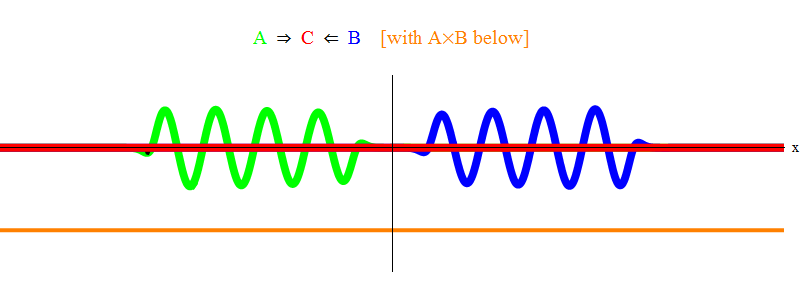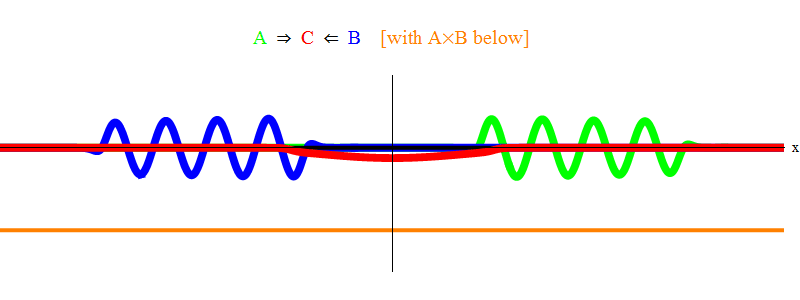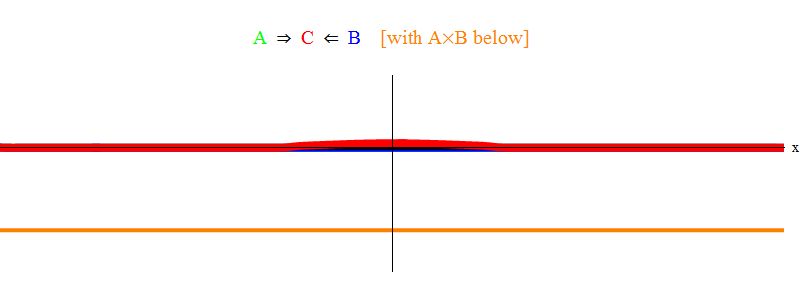Fig. 1

Como um valor diferente de zero de AB afeta C? A resposta é altamente dependente da frequência ν. Primeiro, darei uma resposta pronta e depois uma explicação aproximada do motivo. Isso é, de fato, ressonância . A ressonância é um fenômeno integral de todas as vibrações (vibrações), incluindo as ondas. Eu já descrevi como a bola na mola oscila com uma frequência natural e como a força vibracional que empurra a bola pode levar a ressonância se a frequência da oscilação da força coincidir com a frequência natural da bola na mola.

Tendo compreendido a ressonância, você verá que o campo C, oscilando com uma frequência mínima e velocidade horizontal zero, se comporta como uma bola em uma mola, e AB se comporta como uma força oscilante tentando fazer a bola oscilar. Portanto, o fenômeno de ressonância ocorre se a frequência de vibração AB - 2ν - for a frequência mínima do campo C - ν _min . Mais especificamente:

• Se 2 ν não for igual a ν _min - se a força não estiver em ressonância - então na área onde AB não for igual a zero, C começará a flutuar irregularmente, com uma pequena amplitude.
• Se 2 ν = ν _min - se a força estiver em ressonância -, C irá oscilar suavemente, com uma grande amplitude, na área onde AB não é igual a zero e continuará a flutuar mesmo quando AB voltar a zero.

Fig. 1 mostra apenas a situação ressonante 2 ν = ν _min . Pode-se observar que, quando a onda A passa pela onda B, eles deixam para trás uma onda estacionária C, oscilando com uma frequência vmin. Impressão fina: na fig. um esboço é mostrado, não uma solução exata das equações. A solução exata terá muitos recursos pequenos e complexos que ofuscam o significado físico básico, por isso os excluí para maior clareza. Mais tarde, consideraremos uma situação sem ressonância, que é muito mais complicada, mas também mais importante para a física.

O surgimento de uma nova partícula a partir da aniquilação dos outros dois

Acabei de demonstrar que os termos não lineares AB na equação C podem fazer com que a superposição das ondas A e B produza oscilações do campo C se a soma das frequências dos campos A e B for igual à frequência mínima do campo C. Mas e se essas ondas tivessem amplitude muito pequena? O que pode acontecer se um quantum do campo A encontrar um quantum do campo B?

• Se as frequências AB entrarem em ressonância com o campo C, poderá ocorrer um quantum do campo C, ou seja, uma partícula real C, e os quanta A e B desaparecerão - "aniquilar".
• Além disso, os quanta A e B podem simplesmente passar um pelo outro, sem criar a partícula C.
• As leis da mecânica quântica sugerem que a probabilidade de criar uma partícula C é proporcional ao quadrado de y, que é multiplicado por AB na equação do movimento C.
• Se as frequências não entrarem na ressonância, a partícula real C não aparecerá. No entanto, um distúrbio temporário pode ocorrer no campo C, um exemplo do que é freqüentemente chamado de "partícula virtual" C; nesse caso, os quanta A e B podem desaparecer. Qual é o resultado de tal distúrbio? Descrevi parcialmente esse processo no final do artigo, na seção "caudas".

Este é o estado geral das coisas. Vamos nos aprofundar nos detalhes.

O que para partículas, isto é, quantidades dos campos A, B e C, significa estar em ressonância ou não em ressonância? Vale lembrar que a energia de um quantum está relacionada à sua frequência devido à equação E = h ν. Então, traduzimos nossa discussão sobre ondas em uma discussão sobre partículas.

Suponha que nossas ondas nos campos A e B consistam em cada um de um quantum. Esses quanta são sem massa, uma vez que A e B satisfazem as equações da classe 0. Mais precisamente, os termos lineares em suas equações de movimento são os mesmos da classe 0. Como os quanta A e B têm a mesma frequência, têm a mesma energia, E = h ν. Como o momento de um quantum sem massa é p = E / c, os quanta A e B terão momentos iguais em magnitude a h ν / c, mas opostos em direção, uma vez que um deles se move para a esquerda e o outro para a direita. Portanto:

• A energia total de dois quanta juntos será de 2hν.
• O momento total dos dois quanta juntos será zero.

Como a energia e o momento são conservados, a energia total após a colisão de dois quanta permanecerá igual a 2hν e o momento total permanecerá zero.

No caso das ondas, vimos que, como a equação para C contém um termo da forma AB, há uma ressonância quando a frequência AB (trabalhando como força oscilante) coincide com a frequência mínima C (trabalhando como uma bola em uma mola). Traduzimos essa afirmação em quanta.

A frequência AB será 2 ν, portanto a energia do produto A e B, quando as ondas A e B consistem em um quantum, é igual à soma das energias A e B.

$$

$$E_ {AB} = 2 h \ nu = E_A + E_B$$

A frequência mínima C é igual a ν _min , o que significa que, para um quantum estacionário do campo C, o momento é 0 e a energia

$$

$$E_C = h \ nu_ {min} = mc ^ 2$$

Onde m é a massa do quantum C.

Para ressonância, é necessário 2 ν = ν _min , ou seja:

$$

$$E_A + E_B = 2 h \ nu = h \ nu_ {min} = mc ^ 2 = E_C$$

Em resumo, a ressonância ocorre quando as somas de energias iguais das partículas A e B (em que, no nosso caso, os pulsos são iguais em magnitude e opostos em direção) são suficientes para criar uma partícula estacionária C! No processo, as partículas A e B são aniquiladas - sua energia entra completamente na criação da partícula C. Isso é mostrado (esquematicamente) na Fig. 2, que você precisa comparar com a fig. 1


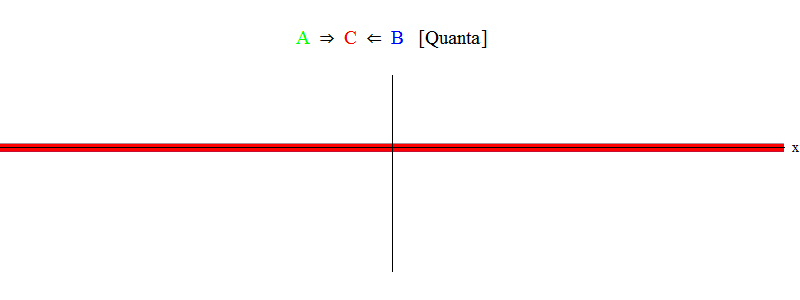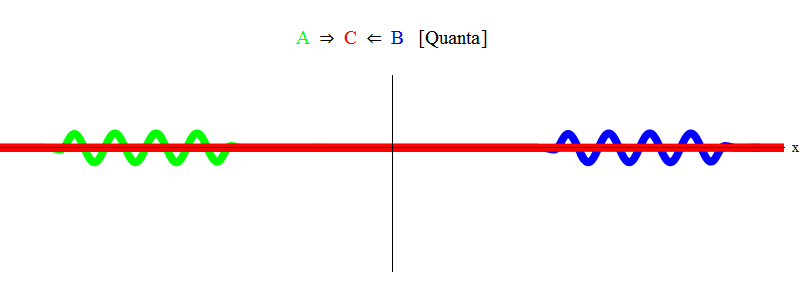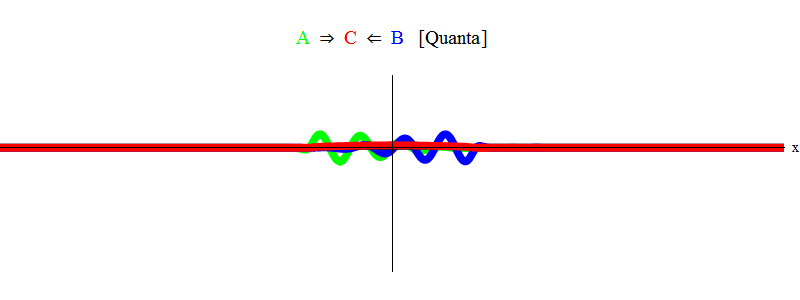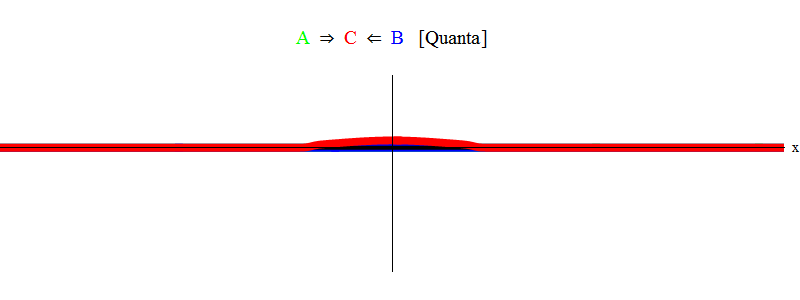Fig. 2

Raciocínio

Acabei de mostrar o processo A + B → C. Na minha explicação, usei três tipos diferentes de partículas para evitar confusão. Mas a mesma ideia permite passar por processos da forma A + A → C (por exemplo, gluon + gluon → a partícula Higgs, e basicamente é assim que a partícula Higgs é obtida no Large Hadron Collider) e processos da forma A + A * → C, onde A * - antipartícula para A (por exemplo, quark + antiquark → partícula Z, e é assim que as partículas Z são geralmente obtidas no LHC). Só é necessário alterar pequenos detalhes, mas a essência permanece a mesma.

Outro processo que representa a mesma idéia, apenas revertida no tempo - a deterioração das partículas. O decaimento de uma partícula de Higgs em dois fótons ou partículas Z em um quark e um antiquark ocorre essencialmente como a animação na Fig. 2, indo na direção oposta.

Caudas

1. Se o termo AB perturba o campo C sem ressonância - se 2 ν ≠ ν _min - o que acontecerá? Lembre-se de que, se você empurrar o balanço com a criança na frequência errada ou aplicar uma força na bola na mola, oscilando com uma frequência que não coincide com a frequência natural das vibrações, você receberá uma vibração desigual com uma pequena amplitude. No contexto atual, o mesmo acontece com o campo C. O campo C se comportará de alguma forma, mas isso não levará à aparência de um quantum C. com bom comportamento. Ele fica um pouco preocupado. Essa má indignação é um exemplo do chamado “Partículas virtuais C” - mas não é uma partícula (quantum de uma onda do campo C), apesar do nome. Sua massa é diferente da massa da partícula C; pode ser maior ou menor. Ao contrário da partícula C, ela não existe por muito tempo. E não satisfaz as condições de amplitude que os quanta reais devem satisfazer. Ao contrário, ao contrário da partícula C, que existe há algum tempo, com a fig. 2, uma perturbação não ressonante existe apenas quando A cruza B.

Mas isso não significa que não afeta nada. Por exemplo, pode fazer com que as partículas A e B saltem uma da outra.

$$

$$A_ \ rightarrow + B_ \ leftarrow → C_ {indignação} → A_ \ leftarrow + B_ \ rightarrow$$

Em geral, no espaço tridimensional, uma recuperação ou dispersão pode levar ao fato de que A se move em qualquer direção e B se move na direção oposta. Exemplos de tais processos incluem a dispersão de elétrons e pósitrons devido a um fóton virtual, ou a dispersão de quarks e antiquark devido a um glúon virtual.

Na presença de outros campos, D e E, interagindo com C e participando da equação de movimento C

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B + y 'D E$$

Processos muito mais interessantes podem ocorrer:

A + B → C _{perturbação} → D + E

É isso mesmo: as partículas A e B podem aniquilar graças à partícula virtual C e levar ao aparecimento de novas partículas D e E. Esta é a segunda maneira de criar novas partículas! Por exemplo, um elétron pode colidir com um pósitron, aniquilar através de um fóton virtual (lembre-se de que isso significa "através de uma perturbação do campo de fótons em uma frequência que não coincide com a ressonante") e se transformar em um múon e antimuon, ou quark e antiquark. O quark inferior e o antiquark superior podem colidir, aniquilar através de uma partícula W virtual e se transformar em elétron e antineutrino. Ou dois glúons podem colidir, aniquilar através de um glúon virtual e se transformar em um quark superior e um antiquark superior (esta é a maneira mais comum de obter quarks superiores em um LHC).

2. E se duas ondas nos campos A e B tiverem frequências diferentes, ν _A e ν _B ? Em frequências adequadas, as partículas C ainda podem aparecer, mas as condições de ressonância serão diferentes e a partícula C criada não será estacionária. Vamos descobrir.

Se eles tiverem frequências diferentes, dois quanta sem massa em colisão terão

• Várias energias $$$E_A = h \ nu_A$ e $$$E_B = h \ nu_B$
• vários impulsos $$$p_A = + h \ nu_A / c$ e $$$p_B = - h \ nu_B / c$ (aqui, mais significa para a direita, menos para a esquerda).

O momento total p _A + p _B agora _é diferente de zero. Mas o momento persiste. Portanto, se a partícula C puder ocorrer como resultado da aniquilação das partículas A e B, ela terá um momento p _C = p _A + p _B , de modo que se moverá para a esquerda ou direita e não ficará parada. Se ν _A > ν _B , ele se moverá para a direita, caso contrário, para a esquerda.

Quanta energia é necessária para criar uma partícula em movimento C? Para isso, é necessária mais energia do que para uma estacionária - como qualquer partícula maciça, sua energia e momento devem satisfazer

$$

$$E_C ^ 2 = (p_Cc) ^ 2 + (mc ^ 2) ^ 2$$

O que significa que E _C = mc ² se p _C = 0 ou mais se o momento for diferente de zero. A lei de conservação de energia e momento nos diz que:

$$

$$E_C = E_A + E_B$$

$$

$$p_C = p_A + p_B = E_A / c - E_B / c$$

Onde consegui a última equação? Para uma partícula sem massa, p = E / c, e para as partículas em colisão A e B, seus momentos são opostos, portanto diferem no sinal. Substitua isso na equação anterior e obtenha:

$$

$$(E_A + E_B) ^ 2 = (E_A - E_B) ^ 2 + (mc ^ 2) ^ 2$$

Os termos E _A ² e E _B ² são mutuamente aniquilados e, movendo os termos E _A E _B para a esquerda, obtemos:

$$

$$4 E_A E_B = (mc ^ 2) ^ 2$$

Dividindo por h ² e usando a relação m = hν _min / c ² , obtemos a condição de ressonância:

$$

$$(2 \ nu A) (2 \ nu B) = \ nu_ {min} ^ 2$$

O que reduz corretamente quando ν _A = ν _B na equação de uma partícula imóvel C, 2 ν = ν _min . Se essa condição não for atendida, a partícula C não poderá ser criada. Se satisfeito, então é possível.

3. Observei que, da mesma maneira que a equação de movimento do campo C contém o termo AB, a equação de B contém o termo AC. Lembre-se destas equações:

$$

$$

Portanto, se a superposição das ondas A e B leva ao aparecimento de uma onda no campo C, tornando-a diferente de zero, como na Fig. 1, precisamos nos preocupar com o fato de que essa nova onda C se sobrepõe à onda existente A e leva a uma mudança no campo B? Eu respondi que "sim, mas podemos negligenciar isso". Podemos negligenciar por causa de uma combinação de duas razões.

Em primeiro lugar, devido ao número "y" que aparece antes das multiplicações de AB e BC. O impacto no campo C do membro AB é proporcional a y vezes A multiplicado por B. O impacto no campo B do membro AC também é proporcional a y vezes A multiplicado por C, mas por sua vez será igual a y ² vezes A multiplicado por por A multiplicado por B. Portanto, enquanto y for menor que 1, y2 será menor que y, portanto o efeito em B do membro AC é pequeno comparado ao efeito em C do membro AB - pelo menos para as pequenas ondas A e B. Na prática, essas as ondas são geralmente pequenas: a partícula A é um quantum da onda no campo A; portanto, a onda A possui amplitudes pequenas d.

Da qual se segue a segunda razão mais estranha, mas mais convincente: vimos que, se um quantum A encontra um quantum B e se transforma em um quantum C, as ondas A e B desaparecem (aniquilam). Após a criação de C, não há mais onda A; portanto, a CA é zero, ou seja, não há efeito no campo B.

E a última captura: embora eu não possa provar isso sem cálculos adicionais, mesmo que as ondas A e B consistam em um quantum, como na Fig. 2, então o processo na Fig. 2 seria muito mais complicado se y fosse muito maior que 1. Portanto, a simplicidade da história que contei exige pequenos valores de y. Na natureza, a maioria dos termos não lineares na física de partículas é geralmente pequena, então o que eu disse se aplica às situações praticamente aplicáveis. As exceções são muito interessantes - elas levam à criação de objetos complexos, como prótons e outros hádrons.