
A física é a ciência complexa mais complexa; é tão complexa quanto fascinante. Se descartarmos o componente matemático, a física se tornará imediatamente disponível para qualquer pessoa com curiosidade e imaginação. Compreenderemos facilmente o conceito da teoria da gravidade, dispensando equações matemáticas complexas. Portanto, para todos que pensam no que torna os mirtilos azuis e os morangos vermelhos; quem duvida que o som se propague sob a forma de ondas; alguém se perguntando por que o comportamento da luz é tão diferente de qualquer outro fenômeno no universo, você precisa entender que tudo está na física quântica.
Este livro apresenta (e desmistifica) para as pessoas comuns o mundo mágico da ciência quântica, como nenhum outro livro. Ela fala sobre conceitos científicos básicos, de partículas de luz a estados da matéria e as causas do impacto negativo dos gases de efeito estufa, revelando cada tópico sem o uso de terminologia científica específica - exemplos da vida cotidiana comum. Obviamente, um livro sobre física quântica não pode prescindir de um conjunto mínimo de fórmulas e equações, mas esse é um mínimo necessário, compreensível para a maioria dos leitores. Segundo o autor, um livro que popularize a ciência deve ser acessível, mas não inferior ao nível do leitor, mas para elevar e desenvolver seu intelecto e nível cultural geral.
Quantum Racquetball e Fruit Color
Uma propriedade chave dos elétrons ligados a átomos e moléculas é que seus estados de energia são discretos. Dizemos que a energia de um elétron pode ser quantizada, ou seja, um elétron ligado a um átomo ou molécula pode ter apenas alguns valores de energia específicos. A energia muda gradualmente, e essas etapas têm certos tamanhos discretos. Os estados de energia são como escadas. Você pode ficar em um passo ou subir para o próximo, mais alto. No entanto, é impossível ficar no meio do caminho entre as duas etapas. Esses valores de energia discretos ou quantizados são freqüentemente chamados de níveis de energia. Diferentemente das escadas comuns, os intervalos entre os níveis de energia geralmente não são os mesmos.
Uma área importante da pesquisa quântica moderna é o cálculo dos estados eletrônicos das moléculas. Essa área é chamada química quântica. Tais cálculos tornam possível obter níveis quantificados de energia para elétrons nas moléculas (níveis de energia), bem como calcular a estrutura das moléculas. O cálculo da estrutura da molécula fornece a distância entre os átomos e as posições de todos os átomos na molécula com uma precisão limitada apenas pelo princípio da incerteza. Assim, os cálculos da mecânica quântica possibilitam determinar o tamanho e a forma das moléculas. Tais cálculos são importantes para a compreensão dos princípios fundamentais da ligação de átomos a moléculas e para a construção de novas moléculas. Com o desenvolvimento da teoria quântica e o surgimento de computadores cada vez mais poderosos e complexos capazes de resolver problemas matemáticos trabalhosos, mais e mais moléculas grandes podem ser estudadas usando os métodos da química quântica. Uma das aplicações mais importantes da teoria quântica é o desenvolvimento de produtos farmacêuticos. As moléculas podem ser projetadas para que tenham o tamanho desejado e “se ajustem” à forma de locais específicos de proteínas ou enzimas.
A química quântica requer cálculos muito trabalhosos. Mesmo para o átomo de hidrogênio mais simples, os cálculos da mecânica quântica são matematicamente muito complicados. Um átomo de hidrogênio consiste em um elétron ligado a um próton. Um próton, que é o núcleo de um átomo de hidrogênio, é uma partícula carregada positivamente e um elétron é carregado negativamente. A atração de um elétron carregado negativamente para um próton carregado positivamente os mantém unidos, mantendo o átomo de hidrogênio unido. Os detalhes do cálculo dos níveis de energia do átomo de hidrogênio não serão apresentados aqui, mas nos próximos capítulos consideraremos algumas características dos resultados desses cálculos. Eles fornecem os níveis de energia do átomo de hidrogênio e suas funções de onda. São as funções das ondas, isto é, as ondas de amplitude de probabilidade para um átomo de hidrogênio, que são o ponto de partida para a compreensão de todos os átomos e moléculas. Átomos e moléculas são complexos porque são sistemas tridimensionais absolutamente pequenos, e é necessário levar em consideração como prótons e elétrons interagem entre si.
Uma partícula em uma caixa - um caso clássico
Há uma tarefa muito simples relacionada ao nosso tópico. É conhecido como o problema de partículas em uma caixa. Não requer matemática complicada para resolvê-lo, mas essa solução nos permite ilustrar propriedades importantes dos elétrons ligados, por exemplo, quantização dos níveis de energia e a natureza ondulatória dos elétrons nos estados ligados. Antes de analisar a natureza do elétron em uma caixa unidimensional de tamanhos atômicos, discutimos o problema clássico de um playground unidimensional ideal para o racquetball para identificar as diferenças entre os sistemas clássico (grande) e mecânico-quântico (absolutamente pequeno).
Na fig. 8.1 descreve a "caixa" perfeita. Ele é unidimensional. Suas paredes são consideradas infinitamente altas, infinitamente maciças e completamente impenetráveis. Não há ar dentro da caixa para resistir ao movimento. Na figura, o interior da caixa é designado Q = 0 e o exterior - Q = ∞. Foi dito anteriormente que uma partícula é chamada livre e que nenhuma força atua nela. As forças surgem quando uma partícula interage com alguma coisa. Por exemplo, uma partícula carregada negativamente, como um elétron, pode interagir com um próton carregado positivamente. A interação na forma de atração entre partículas carregadas de maneira oposta gera uma força atuando no elétron. Ao controlar elétrons em um CRT (veja a Fig. 7.3), um campo elétrico gera uma força que age nos elétrons e os força a mudar de direção.
Uma medida da interação de uma partícula com algo que a afeta, como um campo elétrico, é chamada de potencial e tem a dimensão de energia. No futuro, o potencial será indicado pela letra Q. Dentro da caixa, Q = 0, como no caso de uma partícula livre. Isso significa que a partícula não interage com nada dentro da caixa. Não há campos elétricos ou resistência ao ar. No entanto, fora da caixa, Q = ∞. Potencial infinito significa que uma partícula teria que ter energia infinita para estar em áreas fora da caixa. A expressão Q = ∞ é apenas uma maneira de formalizar a afirmação de que as paredes da caixa são ideais. Uma partícula não pode penetrar através das paredes ou pular sobre elas, por maior que seja sua energia. Se você colocar uma partícula nessa caixa, ela não poderá escapar e sempre permanecerá dentro dela. Nesse sentido, a partícula é trancada em uma caixa. Pode estar em uma região do espaço L de comprimento, mas em nenhum outro lugar.
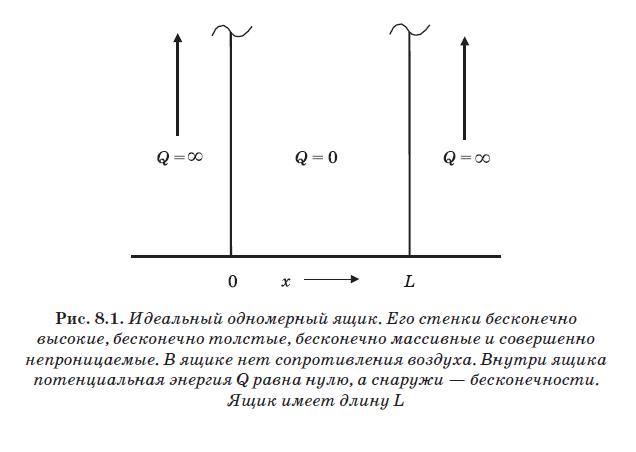
Na fig. A Figura 8.2 mostra uma bola para jogar racquetball, quicando nas paredes de uma quadra ideal (grande) clássica e unidimensional de racquetball. Como já mencionado, essas paredes são ideais, mas não há resistência ao ar no interior. Além disso, a bola também é ideal, ou seja, possui elasticidade absoluta. Quando a bola colide com a parede, ela se contrai como uma mola e se endireita novamente, fazendo com que ela salte. Bolas reais não são perfeitamente elásticas. Quando a bola é comprimida após o impacto, nem toda a energia gasta na compressão é repelida da parede. Parte da energia gasta comprimindo a bola vai aquecê-la. No entanto, aqui consideraremos a bola perfeitamente elástica. Ao bater em uma parede, toda a energia cinética da bola, que faz com que ela se comprima, é gasta em empurrar a bola para longe da parede. Portanto, a velocidade da bola imediatamente antes da colisão com a parede é igual à velocidade de seu rebote após a colisão.
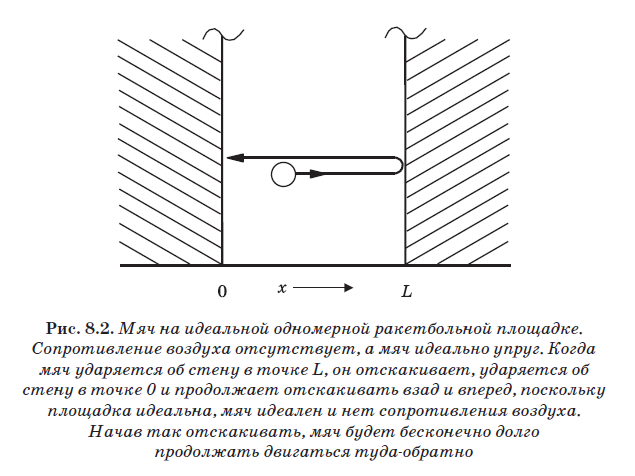
Nesse campo de raquete ideal, a bola quica nas paredes sem perda de energia; além disso, não há resistência do ar nem gravidade. Portanto, a bola sempre se moverá para frente e para trás, refletindo nas paredes. Ele atinge a parede no ponto L, salta, colide com a parede no ponto 0, salta novamente e continua a se mover para frente e para trás. Dentro da caixa, como o potencial é zero (veja a Fig. 8.1), nenhuma força atua sobre a bola. Portanto, sua energia é puramente cinética:
onde m é a massa da bola e V é sua velocidade. Se a bola sofrer influências externas fracas, sua velocidade se tornará ligeiramente mais baixa e o valor Ek também diminuirá levemente. Neste racquetball ideal, a energia pode mudar continuamente. O valor de Ek pode aumentar ou diminuir arbitrariamente, dependendo apenas da força do impacto na bola.
Outra característica importante do racquetball clássico é a capacidade de parar a bola para que ela fique imóvel no chão. Nesta situação, sua velocidade é zero: V = 0. E desde V = 0, então Ek = 0. Em V = 0, o momento também é zero, pois p = mV, portanto, sabemos exatamente o momento. Se a bola estiver no chão (V = 0), então sua posição é conhecida. Se denotarmos essa posição x (veja a Fig. 8.2), o valor de x estará no intervalo de 0 a L. O valor de x não pode assumir nenhum outro valor, pois a bola está na quadra (na caixa) e não pode estar fora de para paredes perfeitas. A bola pode ser colocada em uma posição específica x no chão da quadra, e então sua posição será conhecida com certeza. Esta é uma propriedade de um playground macroscópico, mesmo ideal. Este é um sistema clássico, e nele é possível conhecer de maneira precisa e simultânea o momento pe posição x.
A quadra de raquetebol tem 12 m de comprimento, o diâmetro da bola é de 5,6 cm e seu peso é de cerca de 0,04 kg. Obviamente, o jogo de raquetebol é descrito pela mecânica clássica. Com a ajuda da luz, você pode acompanhar o movimento da bola para frente e para trás sem afetá-los.
Partícula em uma caixa - Quantum Case
O que mudará se nos voltarmos agora para a consideração do racquetball quântico? O local permanece ideal, mas agora seu comprimento não é de 12 m, mas 1 nm (10–9 m). Além disso, a partícula tem uma massa de elétrons de 9,1 10–31 kg e não 0,04 kg. Assim, este é o problema de uma partícula quântica em uma caixa.
Podemos dizer imediatamente que a menor energia de uma partícula quântica em uma caixa do tamanho de nanômetros não pode ser zero. Em um campo clássico de raquetebol, a velocidade da bola V é possível, que é igual a zero, o que significa que o impulso p = mV também pode ser zero. Além disso, a posição da bola x tem um significado claramente definido. Por exemplo, a bola pode ficar parada (V = 0) exatamente no meio da quadra, o que corresponde a x = L / 2. Nesse caso, para o nosso clássico de raquete, ∆p = 0 e ∆x = 0. O valor do produto ∆x∆p = 0 não corresponde ao princípio da incerteza de Heisenberg, o que é normal, pois estamos falando do sistema clássico. No entanto, uma partícula absolutamente pequena em uma caixa do tamanho de nanômetro é um objeto quântico e deve obedecer ao princípio da incerteza, que afirma que ∆x∆p ≥ h / 4. Se V = 0 e x = L / 2, conhecemos x e p, o que significa que ∆x∆p = 0, como no racquetball clássico. Para um sistema quântico, isso não é possível. Assim, V não pode ser igual a zero. Uma partícula não pode permanecer imóvel em um determinado ponto. E se o valor de V for diferente de zero, o valor de Ek não poderá ser igual a zero. O princípio da incerteza diz que a menor energia do nosso racquetball quântico não pode ser zero. Uma bola quântica nunca permanece imóvel.
Valores quânticos de energia das partículas em uma caixa
Que energia uma partícula quântica pode ter em uma caixa do tamanho de nanômetros? Essa pergunta pode ser respondida sem cálculos complicados, mas primeiro precisamos retornar às ondas novamente. No capítulo 6, falamos sobre as funções de onda das partículas livres. A função de onda de uma partícula livre com um momento específico p é uma onda que se estende por todo o espaço. Assim, um elétron com um momento perfeitamente definido é uma onda deslocalizada, cobrindo todo o espaço. A probabilidade de detectar um elétron livre é a mesma em todo lugar. Esse elétron possui uma energia cinética bem definida Ek = 1 / 2mV2, uma vez que possui um momento bem definido p = mV.
O elétron na caixa do nanômetro é semelhante à nossa partícula livre em relação à região interna da caixa, onde Q = 0. Não há potencial dentro da caixa e, portanto, não há forças atuando sobre a partícula. A esse respeito, é muito semelhante a uma partícula livre, sobre a qual nenhuma força atua. No entanto, há uma diferença importante entre a partícula na caixa e a partícula livre - essas são as paredes da caixa. O elétron na caixa está apenas dentro da caixa. A natureza ideal da caixa não permite que sua função de onda se espalhe por todo o espaço. A partícula está dentro da caixa e nunca pode estar fora. A função de onda define a amplitude da probabilidade de detectar uma partícula em uma determinada região do espaço. Esta é uma interpretação de Born da função de onda. Se o nosso elétron puder ser detectado apenas dentro da caixa e nunca fora, então a probabilidade de sua detecção na caixa deve ser finita e fora - zero. Se a probabilidade de encontrar uma partícula fora da caixa for zero, a função de onda deverá ser zero em todos os pontos fora da caixa.
Assim, chegamos à conclusão de que a função de onda de uma partícula em uma caixa é semelhante à função de onda de uma partícula livre, mas a função de onda deve ser zero fora da caixa. Em sua interpretação da natureza da função de onda mecânica quântica, Born impôs algumas restrições físicas à forma que a função de onda pode assumir. Uma delas é que uma boa função de onda deve ser contínua. Esta condição significa que a função de onda deve mudar suavemente de um lugar para outro. Uma mudança infinitamente pequena na posição não pode levar a um salto inesperado na probabilidade. Este é um pensamento muito simples. Se a probabilidade de detectar uma partícula em uma região muito pequena do espaço é, por exemplo, 1%, um deslocamento de um valor inimaginavelmente pequeno não pode subitamente tornar a probabilidade de detectar uma partícula igual a 50%. Isso fica claro nas imagens de pacotes de ondas na Fig. 6.7 A probabilidade varia sem problemas de um lugar para outro. Isso nos permite adicionar algo à descrição das funções de onda de uma partícula em uma caixa, além do fato de serem ondas com amplitudes finitas dentro da caixa e amplitude zero fora. Como a função de onda deve ser contínua, deve ter amplitude zero diretamente na parede da caixa a partir do interior para coincidir com a amplitude zero da função de onda fora da caixa.
Na fig. A Figura 8.3 mostra a descontinuidade (proibida) da função de onda dentro da caixa. A função de onda é indicada (letra grega "fi"). O eixo vertical representa a amplitude da função de onda. A linha tracejada indica seu nível zero. As funções de onda, que são ondas de amplitude de probabilidade, podem variar entre valores positivos e negativos. A função de onda mostrada na Fig. 8.3, possui valores próximos das paredes diferentes de 0. No entanto, a função de onda deve ser zero fora da caixa, ou seja, para valores de x menores que 0 e maiores que L, deve ser zero. Na figura, a função de onda salta inesperadamente de um valor diferente de zero perto da parede dentro da caixa para um valor zero imediatamente atrás da parede fora da caixa. Assim, a função de onda mostrada na Fig. 8.3 não é válido porque não é contínuo. Esta função não pode representar uma partícula quântica em uma caixa.
A função de onda deve ter um valor zero nas paredes
Para que as funções de onda que representam a partícula na caixa sejam fisicamente aceitáveis, seus valores nas paredes devem ser zero e, em seguida, eles não experimentarão um espaço nas paredes. Não é difícil preencher essa condição. A função de onda flutua entre valores positivos e negativos. Cada vez, passando de valores positivos para negativos ou de negativos para positivos, passa pelo zero. De fato, os pontos zero são separados um do outro pela metade do comprimento de onda. Portanto, para obter boas funções de onda de uma partícula em uma caixa, devemos escolher ondas cujo comprimento permita que elas sejam empilhadas na caixa para que os pontos zero fiquem exatamente nas paredes.
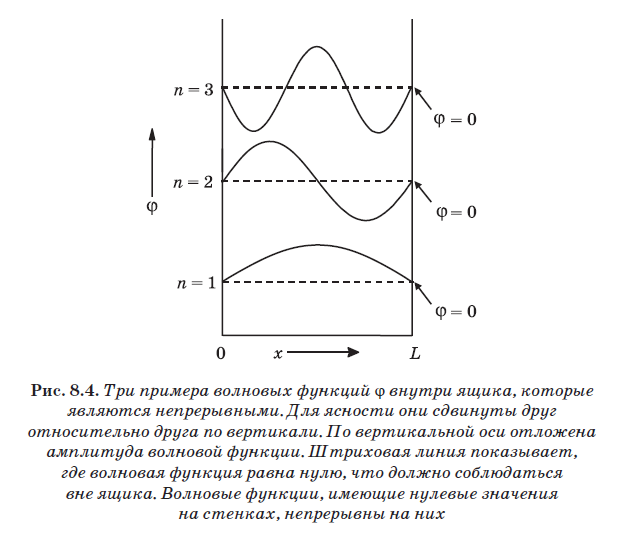
Na fig. 8.4 mostra três exemplos de ondas que são adequadas para o papel das funções de onda para uma partícula em uma caixa. O mais baixo deles é designado n = 1 e consiste em uma meia-onda. Começa à esquerda na amplitude 0, passa o máximo e depois cai para zero na parede no ponto L. A próxima onda, localizada acima e marcada com n = 2, consiste em uma oscilação completa. Também começa na parede esquerda na amplitude 0, passa um pico positivo, retorna a zero, depois um pico negativo segue e retorna a zero na parede no ponto L. A onda indicada por n = 3 contém períodos de um ano e meio. Qualquer onda que contenha um número inteiro de meias ondas, ou seja, 1, 2, 3, 4, 5 e assim por diante, metade do comprimento de onda, e localizada de modo que comece em zero à esquerda e termine em zero à direita, é adequada.
O valor n é o número de meias ondas de uma função de onda específica. Para n = 1, o comprimento de onda é 2L, pois o comprimento da caixa é L e n = 1 corresponde à metade do comprimento de onda. Para n = 2, o comprimento de onda é L, pois exatamente um comprimento de onda é colocado entre as paredes. Para n = 3, três meias-ondas são colocadas entre as paredes, isto é, 1,5 = L. Nesse caso = L / 1,5, isto é, = 2L / 3. Observe que uma regra geral é encontrada aqui: = 2L / n, em que n é um número inteiro. Para n = 1 temos = 2L, para n = 2 - = 2L / 2, para n = 3 - = 2L / 3, etc.
»Mais informações sobre o livro podem ser encontradas no
site do editor»
Conteúdo»
TrechoPara os leitores deste blog, um desconto de 20% no cupom -
Fire