Como o campo Higgs funciona: 2) por que o campo Higgs em média é diferente de zero

Como o campo Higgs funciona:

1. Ideia principal
2. Por que o campo Higgs é em média diferente de zero
3. Como a partícula de Higgs aparece
4. Por que o campo Higgs é necessário

Como é que o campo de Higgs na natureza não possui um valor médio de zero, enquanto outros campos (aparentemente elementares) da natureza que conhecemos possuem zero? [Impressão muito pequena: outros campos, com exceção do campo gravitacional do nível mais baixo, são chamados de métricas, isto permite determinar a existência de espaço e tempo].

Primeiro, os campos de férmion não podem ter um grande valor diferente de zero na natureza. Isto é devido à diferença entre férmions e bósons. Os bósons podem ser, em média, diferentes de zero, mas os férmions não. Então você pode esquecer os elétrons (e seus primos múons e tau), sobre neutrinos e quarks. Letras pequenas: os férmions podem emparelhar-se ou com antifermônios e formar bósons compostos, que podem ser, em média, diferentes de zero. Isso é válido para os quarks superiores e inferiores e seus antiquarks, e para os elétrons em um supercondutor. Mas essa é uma longa história e não diz respeito diretamente à nossa.

E os campos de fótons, glúons, W e Z? Estes são todos os bósons. Em princípio, esses campos poderiam ter um valor médio constante diferente de zero sobre o Universo. Mas experimentos, não teoria, dizem que esse não é o caso. Um valor não zero suficientemente grande do campo elétrico levaria ao aparecimento de vários efeitos, os quais não observamos. O mais importante deles seria uma violação da invariância rotacional em larga escala. O campo elétrico é um vetor (spin-1), indica em uma determinada direção; portanto, se for diferente de zero, a direção na qual esse valor indica deve ser diferente de todos os outros. (Fig. 1, canto inferior esquerdo).


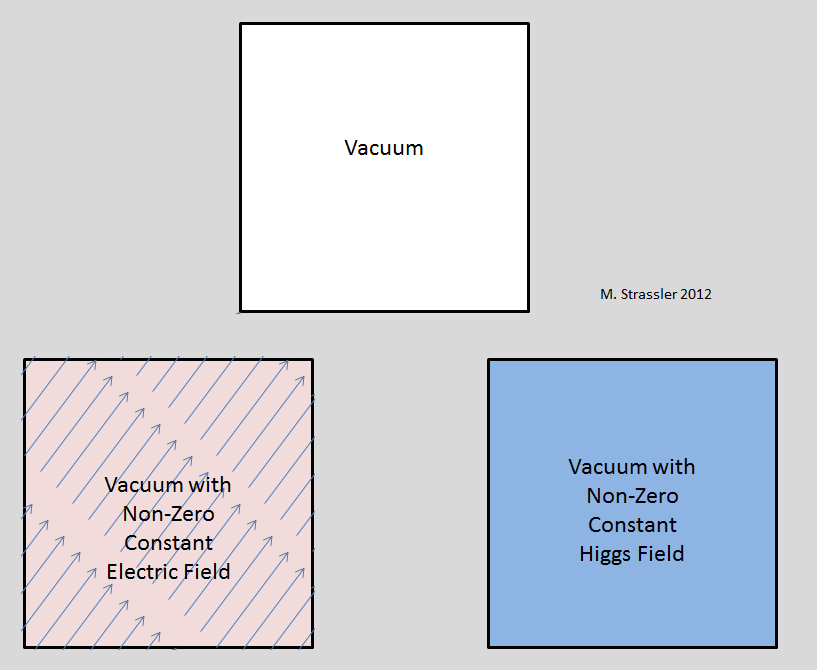Fig. 1

O campo Higgs é escalar (spin-0), não indica nenhum lugar. Entre outros campos escalares (nem elementares nem relativísticos), podemos dar exemplos do campo de densidade do ar, do campo de pressão dentro da Terra e da temperatura do oceano. Em todo ponto no espaço e no tempo, a densidade, a pressão ou a temperatura são apenas um número, e o campo elétrico é um número e uma direção. Portanto, se o campo Higgs tiver um valor diferente de zero, nenhuma direção preferida surgirá - Fig. 1, canto inferior direito. O que é mais estranho (por ser relativístico), o campo Higgs não gera nenhum quadro de referência preferido. Para a densidade do ar, existe um sistema de referência preferido, porque você descansa em relação ao ar ou passa por ele. Mas para o campo de Higgs não é assim; todos os observadores estão descansando em relação a ele. Portanto, o sucesso do SRT de Einstein, que descreve todos os tipos de fenômenos, não contradiz a presença de um campo escalar relativístico de valor diferente de zero, como o campo de Higgs. Resumidamente, na presença de um campo de Higgs diferente de zero, o vácuo se comporta exatamente como se comportaria em H = 0; sua presença pode ser detectada apenas pelo efeito na massa de partículas (ou por algo mais dramático, por exemplo, o uso do LHC para criar partículas de Higgs).

A maneira mais fácil para o campo de Higgs seria manter um valor diferente de zero em todo o Universo se tivesse um valor de equilíbrio diferente de zero H0 participando de sua equação de movimento de classe 1:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - (2 \ pi \ nu_ {min}) ^ 2 (H - H_0)$$

(Deve ser da classe 1, e não da classe 0, por razões que ficarão claras para nós depois de discutirmos a partícula de Higgs). De fato, a situação é um pouco mais complicada. A equação correta ficaria assim:

$$

Onde aeb são constantes (seus quadrados são positivos! Observe o sinal de mais na frente de a ² H e compare-o com o menos na equação anterior), sobre os quais aprenderemos mais adiante. Isso pode ser reescrito como:

$$

$$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - [a / b] ^ 2)$$

Se H (x, t) é uma constante no espaço e no tempo, então dH / dt = dH / dx = 0, portanto

$$

$$0 = - b2 H (H2 - [a / b] ^ 2)$$

(quando H (x, t) é uma constante em x e t), e ele tem soluções (por enquanto, simplificaremos muito tudo):

1. H = 0
2. H = + a / b
3. H = - a / b

Em outras palavras, as posições de equilíbrio são três, não uma. Letras pequenas: simplifico bastante aqui, mas sem prejuízo do significado.

Isso não está claro imediatamente, mas a solução H = 0 é instável. A situação é semelhante à equação de movimento de uma bola em uma tigela da forma mostrada na Fig. 2 - semelhante ao fundo de uma garrafa de vinho. Ele também tem três posições de equilíbrio, uma em 0 e duas em ± x ₀ . Mas, obviamente, a posição em 0 é instável - qualquer empurrão fará a bola vermelha rolar para longe de x = 0, uma mudança importante na situação. Por outro lado, o equilíbrio em x = x _{0 é} estável, pois qualquer empurrão fará a bola verde oscilar com uma pequena amplitude em torno do ponto x = x ₀ - não é uma mudança tão drástica. O mesmo vale para uma bola verde clara em x = -x ₀ . Da mesma forma, embora H = 0 seja a solução para a equação do campo de Higgs, a história do nosso Universo acabou sendo complicada o suficiente para garantir que o campo de Higgs seja corretamente chutado, para que não possa permanecer nessa posição. Em vez disso, o campo Higgs estava em uma solução com um valor diferente de zero e em uma situação estável.



Por décadas, graças a uma combinação de experimentos e teoria, sabíamos que o valor do campo de Higgs (que é tradicionalmente chamado de "v") é 246 GeV. Isso nos dá uma idéia dessas constantes aeb:

a = vb = (246 GeV) b

Assim, podemos determinar a até b, e podemos reescrever a equação de movimento de Higgs:

$$

Mas isso não nos dá uma idéia do próprio b. No próximo artigo, aprenderemos mais sobre ele.

Agora, embora eu tenha preparado tudo para que H seja igual a v ou –v, não importa se o campo de Higgs é positivo ou negativo (de fato, existem ainda mais possibilidades, veja abaixo); o mundo ficará exatamente igual, com a mesma física, pois nada depende do sinal de H. Não se torna óbvio imediatamente, mas é; uma dica - onde quer que você encontre H nas equações que estou descrevendo ou na descrição de como o campo Higgs funciona, H ² aparece em todos os lugares, e não apenas H - e H ² não depende de H = v ou H = -v . [Letras pequenas: de fato, H é um campo complexo, com as partes real e imaginária, portanto H pode ser igual v vezes qualquer número complexo z para o qual | z | = 1; e de fato, H * H = | H | ² , mas não depende de z. E mesmo isso não é tudo! Mas o suficiente por hoje.]

Se você encontrar uma maneira (por exemplo, colidir prótons no Large Hadron Collider) de empurrar ou introduzir perturbação no campo de Higgs, ele irá oscilar para frente e para trás - ou seja, as ondas aparecerão na forma

$$

$$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$$

Onde A é a amplitude da onda, ν e λ são a frequência e o comprimento de onda, e a relação entre ν e λ depende da forma exata da equação do movimento, em particular de be v. Como o campo de Higgs é quântico, a amplitude dessas ondas será quantizada, e o quantum dessas ondas é o que chamamos de partícula de Higgs. Da próxima vez, consideraremos as propriedades dessas partículas.