Olá, meu nome é Alexander e sou físico. Do lado de fora, isso pode parecer um veredicto, mas na verdade é. Descobri que estou fazendo uma pesquisa fundamental em física, ou seja, estudando partículas carregadas aceleradas: prótons e todos os maiores são íons positivos, isto é. Nos estudos, eu não uso aceleradores grandes como LHCs, mas atiro na película com um laser, e um momento de próton voa para fora da película.

Agora, algumas palavras sobre mim. Eu me formei na faculdade de fotônica e opto-informática da ITMO em São Petersburgo, depois fui para uma magistratura na Universidade Aalto (na Finlândia), na direção de micro e nanotecnologia, e depois cuspi em todas essas pequenas coisas, microscópios e especialmente em uma sala limpa. E entrei na ciência fundamental com grandes lasers. Agora trabalho na pós-graduação no sudoeste da Suécia, na cidade de Lund, na universidade de mesmo nome. Trata-se da distância de um tiro de canhão de Copenhague.

Como acelerado, tão voou

Aceleradores de partículas carregadas não são uma idéia nova, mas o método pelo qual eu os acelero é relativamente novo, mais ou menos da mesma idade que eu. Permite reduzir significativamente o tamanho do acelerador e seu custo, incluindo o custo do trabalho e manutenção. A diferença entre os dois tipos pode ser estimada na figura abaixo.

À esquerda, há um acelerador linear eletrostático (levemente desmontado); À direita está o meu pequeno, mas orgulhoso criador de furos

Vamos comparar esses dois padrões de sombrio gênio físico com mais detalhes. Olhe para o acelerador esquerdo e para a direita, depois novamente para a esquerda e novamente para a direita: sim, o meu está em um cavalo (uma piada - comentário do autor). De fato, a mina tem apenas um metro de diâmetro e os prótons são acelerados a partir de um pedaço de papel alumínio. Seu suporte está localizado exatamente no meio do círculo, vestindo uma linda saia de cobre. É muito mais simples e mais compacto que a amostra esquerda, que é do tamanho de um ônibus e, além disso, é preenchida com gás asfixiante. Assim, tendo-se afirmado em abundância (muitas vezes acontece na física que quanto menor, melhor), pode-se recorrer à física do processo de aceleração.

Como aceleramos as partículas carregadas, é mais lógico fazer isso com um campo elétrico. O campo que caracterizaremos pela tensão. Para aqueles que freqüentaram a escola antes e depois da escola, lembre-se: a força do campo elétrico é uma quantidade física vetorial que caracteriza o campo elétrico em um determinado ponto e numericamente igual à proporção da força que age sobre uma carga de ponto fixo colocada em um determinado ponto do campo, a magnitude dessa cobrança (copiar e colar sujo da Wikipedia). Tem uma dimensão de V / m. Voltando à comparação, o acelerador à esquerda acelera prótons para 4 MeV (Megaelétrons-volts), ou seja, 2,77 * 10 ⁷ m / s ou 9,2% da velocidade da luz. Como a carga de prótons é 1 e o comprimento do acelerador é de dois metros, a intensidade do campo será de 2 MV / m. Aqui assumimos que em todos os lugares o campo é direcionado em uma direção e, em geral, estavam muito próximos da verdade. Um acelerador estilizado possui uma força de campo da ordem de várias TV / m, ou seja, cerca de um milhão de vezes mais. Ainda assim, vale a pena reconhecer que seu comprimento é de apenas alguns mícrons.

Então, neste ponto, descobrimos cujo campo é mais íngreme. É hora de recorrer aos mecanismos físicos e de engenharia que esse campo cria. No caso de um acelerador convencional, existem duas chapas de metal, uma das quais é carregada negativamente e a segunda de forma alguma. Lembre-se do experimento da escola sobre esfregar um pedaço de lã com um pedaço de ebonite. Aqui o princípio é exatamente o mesmo, mas a execução é muito mais complicada. Se você acelerar os prótons da folha, o campo será criado por elétrons, os elétrons voam para fora do plasma quente, o plasma é obtido e aquecido por um laser, e sobre tudo isso no restante do post.

Você quer que eu bata nele, e ele fica roxo em uma mancha?

Se você bater com força suficiente, poderá ver muitos fenômenos físicos maravilhosos. Foi assim que os funcionários de Harvard obtiveram hidrogênio metálico e o perderam.

No meu caso, tiro a folha com um laser. Vou descrevê-lo com mais detalhes depois de explicar a física não trivial dos processos de obtenção de matéria densa e quente, que é exatamente o nome do plasma em termos científicos, responsável pelo triunfo da aceleração dos meus prótons. E agora, as primeiras coisas primeiro.

O laser gera pulsos com comprimento de onda de 800 nm e 35 fs por uma duração (10 ^-15 s), ou seja, o comprimento real do pulso no vácuo é de aproximadamente 10 μm. Cerca de 2 J de energia são jogados nesse impulso, e isso é muito. Se tomarmos esse impulso e o focalizarmos em uma lâmina em um ponto redondo puro de 5 mícrons de diâmetro, a intensidade será da ordem de 10 ²⁰ W / cm2. Isso é muito indecente. Mais uma vez, algumas comparações: o aço pode ser facilmente cortado a uma intensidade de 10 ⁸ W / cm ² (mais ou menos).

De fato, devido às características de design do amplificador, o pulso do laser possui um pedestal anterior que dura aproximadamente 500 ps, e esse pedestal ajuda muito a acelerar bem os prótons.

Ionizado - significa armado

Lembre-se do que acontece com a luz quando ela entra em uma substância. A energia deve ser conservada, o que significa que existem apenas três variantes de eventos: reflexão, transmissão e absorção. Na vida dura, todos os itens acima estão presentes de uma só vez. No estágio inicial, estamos interessados em absorção.

Então, nós temos um pedestal, que também focamos perfeitamente em um pedaço de papel alumínio, e ele é perfeitamente absorvido lá. Para não entrar na complexidade da física do estado sólido, consideramos a absorção de um átomo independente. Da mecânica quântica, sabemos que apenas um fóton pode ser absorvido, cuja energia é exatamente igual à energia da transição de um elétron de um estado para outro. Se a energia do fóton for maior que a energia da ionização (isto é, enviar um elétron do ninho dos pais para uma viagem livre), o excesso será transferido para a energia cinética do elétron, tudo será simples. No nosso caso, fótons com comprimento de onda de 800 nm não possuem energia suficiente (esta é a energia de um fóton, não o pulso inteiro!) Para ionizar o alvo, mas aqui a física vem em nosso auxílio. Lembre-se, eu mencionei uma maior intensidade de radiação? Se, em apêndice, ainda lembramos que a luz pode ser representada como um fluxo de fótons, e a intensidade é diretamente proporcional a ela, então o fluxo de fótons é muito grande. E se o fluxo for tão grande, é provável que vários fótons cheguem ao mesmo local e ao mesmo tempo, e quando sua energia for absorvida, eles aumentarão e a ionização ainda ocorrerá. Curiosamente, esse fenômeno é chamado de ionização multifotônica, e nós o usamos regularmente.

No momento, temos que os elétrons foram arrancados com sucesso, o que significa que o pulso principal chega ao plasma final e começa a aquecê-lo.

Fundamentos da física do plasma (não surgiu uma piada, ah)

Antes do aquecimento, vale a pena conversar um pouco sobre o plasma como um estado da matéria. O plasma é como um gás, apenas elétrons são separados e núcleos são separados. Vamos considerar nosso plasma um gás quase ideal, mas consistindo de elétrons.

Nossa principal característica de um plasma será sua densidade (o número de elétrons por unidade de volume), esse valor será indicado por $ n_e $ (não deve ser confundido com o índice de refração!), E a temperatura desses mesmos elétrons, ou seja, sua velocidade média. Isso é descrito pela distribuição de Boltzmann da mesma maneira que no curso de física da escola:

$$ exibir $$ \ frac {m_e v ^ 2} {2} = \ frac {1} {2} k_B T_e, $$ exibir $$

onde facilmente segue

$$ display $$ \ langle v \ rangle = \ sqrt [] {k_B T_e / m_e}, $$ display $$

onde

$ inline $ k_B $ inline $ - constante de Boltzmann

$ inline $ T_e $ inline $ A temperatura do elétron e

$ inline $ m_e $ inline $ É a massa do elétron. Sim, consideramos aqui um caso unidimensional, mas na verdade não precisamos mais descrever nossos processos.

Agora aplicamos um campo elétrico ao plasma já descrito. Deixe-me lembrá-lo de que o plasma consiste de partículas carregadas, o que significa que, a uma dada densidade, a uma certa distância do local onde aplicamos o campo, os elétrons obscurecem (protegem) a fonte (uma multidão de pequenos Matrosovs - nota do autor). A distância necessária para isso é chamada de comprimento de Debye e é dada pela equação

$$ display $$ \ lambda_D = \ sqrt [] {\ frac {\ epsilon_0 k_B T_e} {q ^ 2_e n_e}}. $$ display $$

Aqui

$ inline $ q_e $ inline $ obviamente a carga de um elétron e

$ inline $ \ epsilon_0 $ inline $ - constante dielétrica do vácuo, uma constante tão fundamental. Analisamos um pouco essa fórmula para ver a física simples do processo. Aumentando a densidade dos elétrons, reduzimos a distância média entre eles; como resultado, para uma distância menor, coletamos elétrons suficientes para proteger completamente nosso campo. Por outro lado, quanto maior a temperatura, maior a distância média entre os elétrons.

Devido ao efeito de triagem e a uma temperatura média bem definida dos elétrons (dependendo da temperatura), o plasma não reage instantaneamente a um campo que chega repentinamente. É lógico supor que o tempo de resposta esteja relacionado ao comprimento do Debye e à velocidade do elétron. Uma boa analogia é jogar uma pedra no lago. Comparado a um lago inteiro, a pedra atua na superfície da água no sentido horário. Parte da água muda imediatamente (é aqui que ela cai), e então as ondas começam a se espalhar pela superfície da água. No caso do plasma, um campo elétrico que aparece repentinamente é uma pedra. O tamanho da pluma é determinado pelo comprimento da blindagem (o campo não age além dela), e a propagação das ondas depende de quão próximos os elétrons estão uns dos outros. Podemos introduzir uma característica como o tempo de resposta do plasma:

$ inline $ t_D = \ lambda_D / v $ inline $ . Em geral, ele nos mostra o tempo durante o qual as informações sobre uma mudança no campo aplicado atingem os elétrons que, por assim dizer, não os viram.

Como somos físicos, não gostamos muito de tempo. É muito mais conveniente trabalhar com frequências, por isso introduzimos o conceito de frequência natural de um plasma. Este valor nos mostrará quantas vezes podemos mudar o campo para que todo o acúmulo de elétrons, que orgulhosamente chamamos de plasma, tenha tempo para responder a essas mudanças. Bem, o que poderia ser mais fácil? Divida a unidade pelo tempo de resposta e aqui está - a frequência:

$$ display $$ \ omega_p = \ frac {1} {t_D} = \ sqrt [] {\ frac {q ^ 2_e n_e} {\ epsilon_0 m_e}}. $$ display $$

É fácil ver que a auto-frequência das oscilações plasmáticas depende da densidade eletrônica. Quanto mais elétrons, maior a frequência. Você pode desenhar outra analogia, mas desta vez com um pêndulo de mola. A alta densidade de elétrons nos diz que eles estão mais próximos, o que significa que eles interagem mais fortemente. Supomos que sua interação em proporção direta esteja associada à elasticidade da mola do pêndulo. E quanto maior a elasticidade, maior a frequência de oscilação.

A frequência natural de um plasma também determina seu índice de refração. Para ser honesto, escrevemos a equação de onda do movimento coletivo de elétrons em um plasma e assumimos pequenas mudanças na densidade de elétrons (não faremos isso aqui porque é chato), depois definimos o índice de refração da seguinte forma:

$$ exibir $$ \ eta = \ sqrt [] {1- \ frac {\ omega ^ 2_p} {\ omega ^ 2_0}}. $$ display $$

Aqui

$ inline $ \ omega_0 $ inline $ É a frequência circular do campo elétrico aplicado. Ela está em rad / se não em Hz!

Nós olhamos cuidadosamente para essa expressão. Como físico experimental, não bebo almas em números reais, mas tento ignorar outras complexas, especialmente o índice de refração complexo. Bem, como a luz, no final, pode se propagar na matéria vezes mais lenta que no vácuo? Isso é algum tipo de bobagem! Não realmente, mas mais sobre isso em outra hora. Se

$ inline $ \ omega_0> \ omega_p $ inline $ , então a expressão tem um significado real e um campo elétrico alternado se propaga dentro do nosso plasma. Todo mundo está feliz, e chamaremos esse plasma de insuficientemente denso. No entanto, se

$ inline $ \ omega_0 <\ omega_p $ inline $ , o índice de refração se torna não apenas complexo, mas inteiramente imaginário. Nesse caso (e não apenas porque eu queria), a onda não se propagará para lá, mas será imediatamente refletida sem perdas. Este é um plasma muito denso. Um fenômeno muito legal, a propósito. É chamado de espelho de plasma.

E como sobremesa

$ inline $ \ omega_0 = \ omega_p $ inline $ . Este é um plasma de densidade crítica. Nesse caso, ele começa a entrar em ressonância com um campo elétrico alternado forçador (fornecido por nós). Para um caso tão especial, você pode até introduzir o conceito de densidade crítica e defini-lo assim:

$$ exibir $$ n_c = \ frac {\ epsilon_0 m_e \ omega ^ 2_0} {q ^ 2_e}. $$ display $$

Naturalmente, a densidade crítica é diferente para cada frequência do campo forçador.

CHOQUE! Aquecimento a plasma! Para fazer isso, apenas ...

No nosso caso, focaremos apenas um mecanismo de aquecimento que prevalece no experimento.

Para começar, deixe o plasma que formamos pelo pedestal tenha um gradiente de densidade suave; nesse caso, temos aquecimento por absorção de ressonância. Uma ilustração disso na imagem abaixo.

Ilustração do processo de absorção de ressonância: a) distribuição da densidade de elétrons perto da frente do alvo; b) refração de um raio laser em plasma com gradiente de densidade; c) o campo elétrico no plasma

Portanto, o laser brilha em nosso plasma em ângulo, bem, deixe-o em 45 graus e, ao mesmo tempo, é polarizado no plano de incidência. A polarização é indicada por setas vermelhas na figura. Nosso plasma tem um gradiente de densidade, o que significa que seu índice de refração está constantemente mudando (aqui está crescendo). Em algum momento, acontecerá que uma determinada camada de plasma do nosso laser se torne "rotativa" e reflita, ou seja, por algum tempo se propagará paralelamente à camada crítica. É importante notar que ele girará antes de atingir a camada de densidade crítica, uma vez que a lançamos em ângulo com o normal. A densidade do plasma na qual o raio laser gira é dada por esta equação:

$$ display $$ n_t = n_c \ cos ^ 2 \ alpha, $$ display $$

onde

$ inline $ n_c $ inline $ A densidade crítica e

$ inline $ \ alpha $ inline $ - ângulo de incidência da luz.

Agora a diversão começa. Lembre-se de que a luz não é apenas um fluxo de fótons, mas também uma onda eletromagnética, ou seja, nosso momento tem um campo elétrico que oscila harmoniosamente com uma grande amplitude. Quando a luz se propaga paralelamente à camada crítica, forma-se uma onda estacionária, que não muda com o tempo (naturalmente, desde que o pulso do laser esteja no lugar). O campo dessa onda, de fato, penetra além da camada de plasma onde a luz se transformou e atinge a camada crítica. Deixe-me lembrá-lo que a frequência das oscilações do plasma na camada crítica é a mesma que a frequência da radiação laser, o que significa que ocorre ressonância. Quando o laser parou de brilhar, a energia que ele comunicou aos elétrons na camada crítica é distribuída através de impactos nos outros elétrons, o que significa que o plasma é aquecido.

Então, onde está, de fato, a aceleração?

Agora que aquecemos os elétrons no poço de plasma e o laser não está mais brilhando, podemos dizer como os prótons são acelerados. Para fazer isso, veja as figuras abaixo. Até este ponto, eu nunca disse de onde os prótons vieram. Naturalmente, eles não aparecem nos núcleos do material da folha. Como não somos muito arrumados e não usamos luvas (as mãos suam muito nelas), água e hidrocarbonetos estão na superfície da folha. O hidrogênio ionizado é nossa fonte inestimável de prótons. Verificado: se você remover a poluição, não haverá prótons.

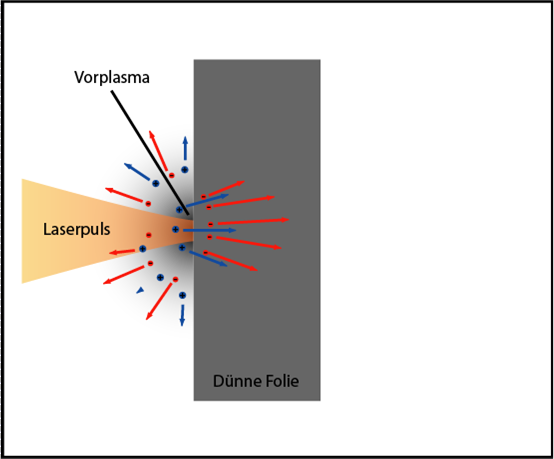	A formação de plasma por um pedestal, isto é, ionização da frente do alvo. Como alvo, geralmente é usada uma folha com uma espessura de 0,4 a 12 mícrons.
	Aqui, a parte principal do pulso interage com o plasma criado e o aquece. Alguns elétrons se aqueceram tão bem que voam da parte de trás do alvo.
	Quando muitos elétrons voam, a carga positiva restante na folha os puxa de volta. No plasma, eles novamente esquentam e voam. Por um tempo, um equilíbrio dinâmico é estabelecido. O campo elétrico é direcionado perpendicularmente ao alvo
	Esse campo muito elétrico separa prótons e outros íons (dependendo do que estava lá) da superfície traseira do alvo e os acelera. Quando os íons se aceleram, a nuvem de elétrons já está caindo e todas as partículas começam a voar mais juntas. E então começamos a acreditar que eles não interagem mais.

Dividir e conquistar

No momento, a posição é a seguinte: o laser não brilha há muito tempo, há um buraco na folha, prótons com elétrons são amigáveis voando do alvo normalmente para a superfície traseira. Não precisamos de elétrons, é por isso que um ímã vem em nosso auxílio. Quando um feixe de partículas carregadas voa através de um campo magnético, as forças de Lorentz de cada partícula são desviadas na proporção de sua velocidade e carga. Consequentemente, prótons e elétrons se desviarão em direções diferentes, e simplesmente não olharemos na direção dos elétrons. A propósito, quanto maior a energia do próton (ou seja, sua velocidade), menor será o desvio. Isso significa que, ao colocar uma tela sensível aos prótons, podemos ver as energias dos prótons acelerados. Mais algumas comparações em números: um ímã que permanece conosco permanentemente e cria um campo de cerca de 0,75 T; em dispositivos de ressonância magnética, o campo magnético é de 1,5 a 3 T.

Além disso, podemos ver o perfil de um feixe de prótons voadores. É redondo, a propósito. E se também pudermos medir a energia de prótons em cada parte do feixe, podemos restaurar de forma exclusiva a forma da nuvem de elétrons, que acelerou nossos prótons.

Em vez de uma conclusão

Uma pergunta justa pode surgir, por que tudo isso é necessário. Minha resposta favorita é exatamente assim. , . , - , — - , , .

, , . , . 80 . , -. , , , , .

. , . , : ( ), ( , , ), ( , ). , , . , , , . , . . , , , . , - , , . , .

, , . , , , 2 ? , . , , .

( , ?), . ( ), , , . 10 . , , 10 , .

Existem duas maneiras de lidar com alta intensidade. Como você pode adivinhar facilmente a partir de sua definição, você precisa aumentar a área ou reduzir a potência. Com o primeiro, tudo fica muito claro, mas o segundo método foi um avanço na tecnologia a laser no século XX. Se o impulso for inicialmente muito curto, ele pode ser esticado, reforçado e comprimido novamente.

, , . , ( , ), . , , , , . , ! ( Chirped Pulse Amplification CPA).

, — , , !

.