Como o campo de Higgs funciona: 3) como a partícula de Higgs aparece

Como o campo Higgs funciona:

1. Ideia principal
2. Por que o campo Higgs é em média diferente de zero
3. Como a partícula de Higgs aparece
4. Por que o campo Higgs é necessário

Em um artigo anterior, descrevi como e por que o campo Higgs não tem um valor médio de zero. Agora, quero descrever o que é uma partícula de Higgs e como sua massa surge das equações.

Quero lembrar que, se o contrário não for mencionado, sempre descrevo a forma mais simples possível do campo e da partícula de Higgs - a chamada Modelo Padrão Higgs. Formas mais complexas também são possíveis; por exemplo, vários campos de Higgs podem existir simultaneamente, em vez de um. Talvez eu descreva um caso mais complexo em um dos seguintes artigos.


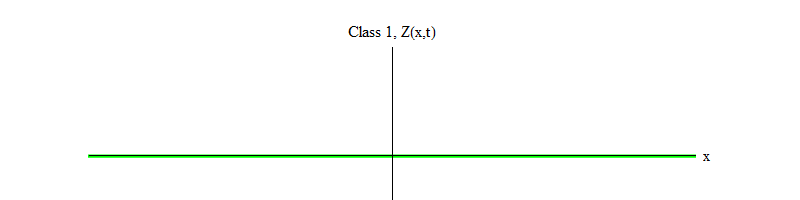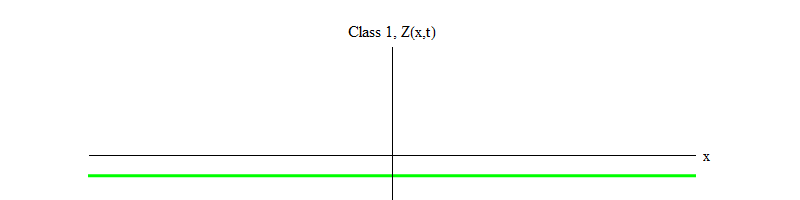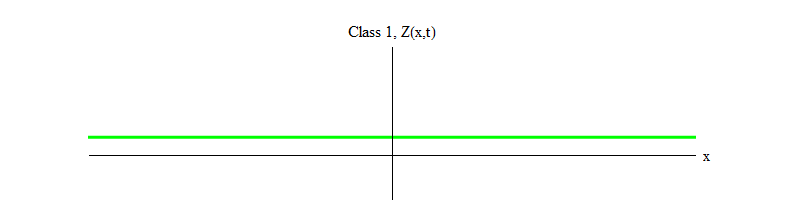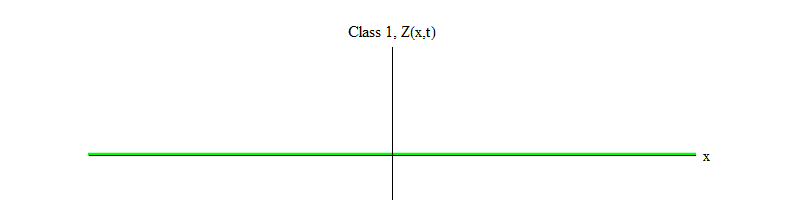Fig. 1: um campo da classe 1 flutua no tempo em torno de um valor estável Z (x, t) = 0

No último artigo, não enfatizei esse fato, mas entre os campos elementares que descobrimos na natureza, o campo de Higgs é único. Todos os campos, exceto Higgs, satisfazem as equações de movimento da classe 0 ou 1. Na verdade (embora provavelmente não seja o caso de todos os campos da natureza), todos os campos que sabemos que satisfazem as equações da classe 1 fazem isso porque o campo Higgs é diferente de zero . Se fosse zero, todos eles satisfariam as equações da classe 0 (como expliquei no primeiro artigo). Em vez disso, o campo Higgs satisfaz uma equação que pode ser chamada de equação da classe -1.

Para o campo Z (x, t), as classes que defini são assim:

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - B ^ 2 Z \ quad [Classe 1 - maciça \; partículas] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0 \ quad [Classe 0 - sem massa \; partículas] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = + B ^ 2 Z \ quad [Classe -1 - instável]$$

As equações implicam que B ² > 0.


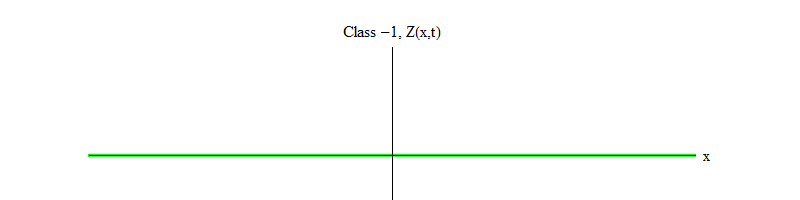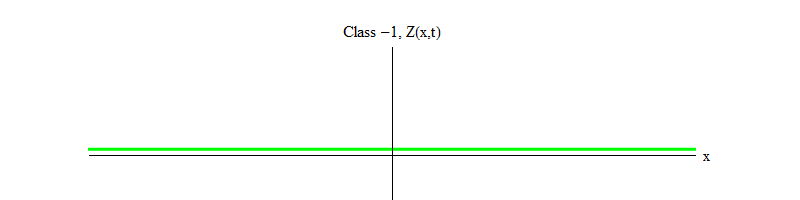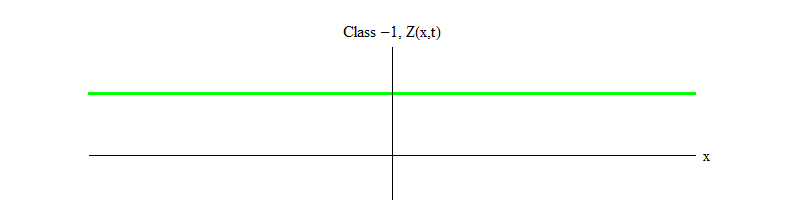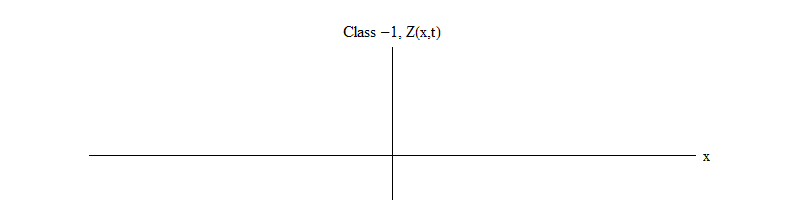Fig. 2: Um campo da classe -1 deixa o equilíbrio instável Z (x, t) = 0.

O sinal de menos entre a classe 1 e a classe -1 é muito importante. Nos dois casos, as soluções das equações contêm Z (x, t) = 0 como um dos casos especiais, mas para a classe 1 Z (x, t) = 0 é estável, ou seja, Z (x, t) pode flutuar em torno de zero; estas estão decentemente comportando ondas com um quantum massivo. E vice-versa, a classe -1 Z (x, t) = 0 é instável, ou seja, Z (x, t) não flutua, mas cresce para valores cada vez maiores. Se você não alterar a equação, a magnitude do campo voará até o infinito. Mais precisamente, se a solução para a equação da classe 1 for a oscilação Z, como na Fig. 1, a solução para uma equação da classe -1 é um crescimento exponencial de Z, como na Fig. 2)

Para o campo Higgs, assim como para qualquer campo existente na natureza, a equação da classe -1 é alterada usando termos que limitam o crescimento exponencial e impedem o campo de ir para o infinito. Como vimos no artigo anterior, o campo Higgs obedece à equação do movimento

$$

Pertence à classe -1 quando H é quase zero, mas possui um membro importante de H ³ . Aqui b é um número positivo e v é a posição de equilíbrio para H. Essa equação garante que, se o campo H começa no ponto H = 0 e se move da posição de equilíbrio instável para H positivo, oscilará em torno da posição de equilíbrio estável em H = v (fig. 3).


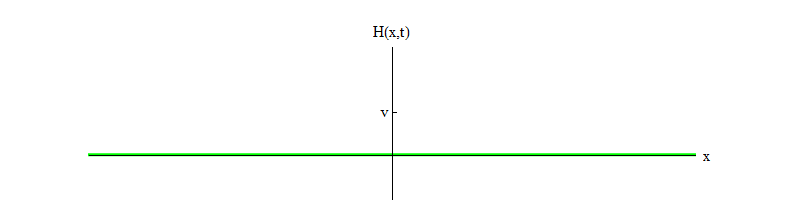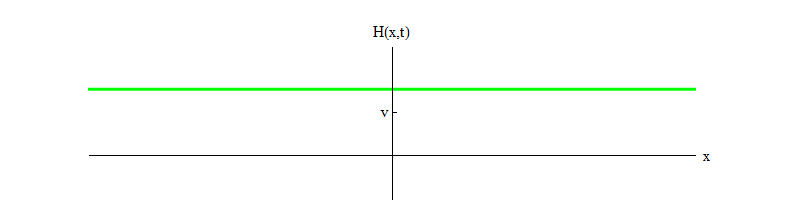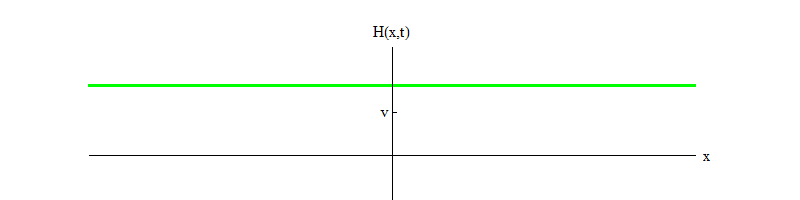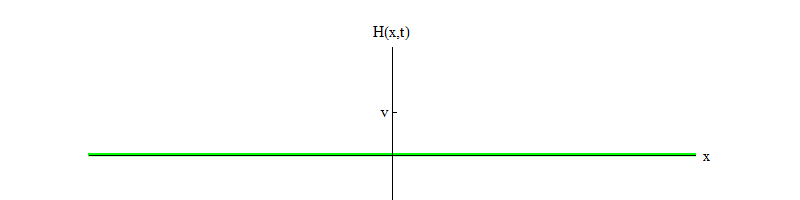Fig. 3

Com o tempo, as oscilações desaparecerão, devido aos termos da equação do movimento, que eu omiti por brevidade; eles permitem que parte da energia das oscilações do campo H seja transferida para ondas de outros campos (esses são os mesmos termos não lineares que permitem que as partículas de Higgs se deteriorem ). Com o tempo (Fig. 4), o campo H se acalma na posição H = v.


Fig. 4

Se algum processo físico derrubar o campo da posição H = v em uma pequena região do espaço, o campo emitirá ondas da forma

$$

$$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$$

Onde A é a amplitude da onda, ν e λ é sua frequência e comprimento de onda, e a relação entre ν e λ depende da forma exata da equação do movimento, em particular de be v. E os quanta dessas ondas serão as partículas de Higgs. Pergunta por milhão: qual é a massa da partícula de Higgs? Para calcular isso, precisamos, como sempre é necessário para partículas (representando quanta de onda em campos relativísticos), determinar a relação entre a frequência ν e o comprimento de onda λ das ondas do campo correspondente e, em seguida, multiplicar o resultado pela constante de Planck h para obter a razão entre a energia e o momento quântico dessas ondas, que nos dirá a massa do quantum (ou seja, partículas).

Fazemos exatamente isso com o campo S (x, t) mencionado no primeiro artigo . Escrevemos uma versão deslocada do campo de Higgs, expressando-a como H (x, t) = v + h (x, t) , e a substituímos na equação de movimento do campo H. h (x, t) escreverei em negrito para distingui-lo da constante h de Planck. No exemplo do campo S dado no artigo de revisão, é indicada uma simples equação de movimento, de modo que a mudança não alterou a massa da partícula S. Mas, neste caso, não é! Como a equação de movimento do campo de Higgs é mais complexa, a equação para h é muito diferente da equação original para H:

$$

$$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - b ^ 2 (v + \ textbf {h}) (2 v \ textbf {h} + \ textbf {h} ^ 2)$$

Onde eu usei o fato de que v é uma constante e é independente do espaço e do tempo. Então, lembramos que o quantum do campo de Higgs tem uma pequena amplitude; portanto, ao estudar a única partícula de Higgs (que é exatamente o que precisamos para determinar sua massa), podemos descartar todos os termos proporcionais a h ² e h ³ :

$$

$$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - 2 b ^ 2 v ^ 2 \ textbf {h} + ...$$

Onde "+ ..." lembra membros descartados. Observe que essa equação para h (x, t) pertence à classe 1, embora tenhamos começado com uma equação de classe -1 para H (x, t); isso ocorre porque H (x, t) era instável na região de H = 0, e h (x, t) era estável na região de h = 0, onde H = v. Portanto, podemos calcular a massa m _{h da} partícula Higgs h usando a seguinte forma de uma equação da classe 1:

$$

$$m_h = \ sqrt2 (h / 2 \ pi) b v / c ^ 2$$

h no lado direito denota a constante de Planck. Se a partícula semelhante a Higgs que foi encontrada recentemente no LHC realmente é a partícula Higgs do Modelo Padrão, então pela primeira vez podemos descobrir o que é b (lembre-se de que v já sabíamos há muito tempo) e, finalmente, podemos descobrir o valor a = b v.

• v = 246 GeV;
• m _h ≈ 125 GeV / c² (se a nova partícula for Higgs)
• b ≈ 0,35 (2 π / h) (se a nova partícula for a Higgs do Modelo Padrão)
• a = bv ≈ 87 GeV (2 π / h) (se a nova partícula for a Higgs do modelo padrão)

onde h, novamente, é constante de Planck. E as três últimas quantidades não eram conhecidas até a recente descoberta da partícula de Higgs.

Agora, se o Modelo Padrão não corresponder à natureza (se, além de H (x, t), for necessário adicionar campos adicionais aos campos conhecidos para explicar as propriedades de uma partícula recentemente descoberta de massa de 125 GeV / c²), vamos assumir que essa partícula é uma das várias tipos de partículas de Higgs - então teremos que lidar com essa situação difícil no LHC por mais alguns anos. Você pode imaginar muitas possibilidades, e não há sentido em explicá-las a todos, mas aproximadamente eu descrevi algumas delas aqui; e se os dados recebidos no LHC nos mostrarem uma certa direção, explicarei tudo em detalhes.