A mecânica clássica é intuitiva: é usada diariamente e repetidamente pelas pessoas para sobreviver. Mas até o século XX, ninguém jamais havia usado a mecânica quântica. Ela descreve coisas tão pequenas que elas caem completamente da percepção dos sentidos humanos. A única maneira de entender essa teoria, de apreciar sua beleza, é bloquear nossa intuição com a matemática abstrata.
Leonard Sasskind - um famoso cientista americano - convida você para uma emocionante jornada ao país da mecânica quântica. No caminho, você precisará de conhecimentos básicos do curso de física da escola, bem como os conceitos básicos de análise matemática e álgebra linear. Você também precisa saber algo sobre as questões abordadas no primeiro livro de "mínimo teórico" de Susskind - "Tudo o que você precisa saber sobre a física moderna". Mas é sem medo que esse conhecimento seja esquecido. Muitos autores irão lembrar e explicar ao longo do caminho.
A mecânica quântica é uma teoria incomum: de acordo com seus postulados, por exemplo, podemos saber tudo sobre o sistema e nada sobre suas partes individuais. Einstein e Niels Bohr discutiram muito sobre essa e outras contradições. Se você não tem medo de dificuldades, tem uma mente inquisitiva, é tecnicamente competente, sincera e profundamente interessada em física, então este curso de palestras de Leonard Sasskind o atrairá. O livro enfoca os princípios lógicos da teoria quântica e não visa suavizar o paradoxo da lógica quântica, mas atraí-la para a luz do dia e tentar lidar com as questões difíceis que ela suscita.
Visão geral da função Wave
Nesta palestra, usaremos a linguagem das funções de onda, então vamos fazer uma breve revisão do material antes de mergulhar. Discutimos na aula 5 as funções de onda de objetos abstratos, sem explicar como eles se relacionam com ondas ou funções. Antes de preencher essa lacuna, lembro o que discutimos anteriormente.
Para começar, escolhemos um L observável com valores próprios le vetores próprios | l〉. Seja Y um vetor de estado. Como os autovetores do operador hermitiano formam uma base ortonormal completa, o vetor | Y〉 pode ser expandido nesta base:
Como você se lembra das Seções 5.1.2 e 5.1.3, as quantidades Y (l) são chamadas de função de onda do sistema. Mas note: a forma específica de Y (l) depende do L específico observável que selecionamos originalmente. Se escolhermos outro observável, a função de onda (juntamente com os vetores base e autovalores) será diferente, apesar do fato de ainda estarmos falando sobre o mesmo estado. Portanto, devemos fazer uma reserva de que Y (l) é a função de onda associada a | Yñ. Para ser mais preciso, devemos dizer que Y (l) é a função de onda na base L. Se usarmos as propriedades de ortonormalidade dessa base de vetores 〈li | lj〉 = dij, a função de onda nessa base L também pode ser definida usando os produtos internos (ou projeções) do vetor de estado | Y〉 pelos vetores próprios | l〉: Y (l ) = 〈L | Y〉
Existem duas maneiras de pensar sobre a função de onda. Primeiro de tudo, este é um conjunto de componentes do vetor de estado em uma base específica. Esses componentes podem ser escritos na forma de um vetor de coluna:
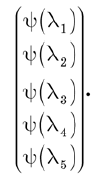
Outra maneira de pensar sobre a função de onda é considerá-la como uma função de l. Se você definir qualquer valor válido de l, a função Y (l) fornecerá um número complexo. Assim, podemos dizer que Y (l) é uma função de valor complexo da variável discreta l. Com essa consideração, os operadores lineares se tornam operações que se aplicam a funções e fornecem novas funções.
E mais um último lembrete: a probabilidade de o experimento dar o resultado l é igual a P (l) = Y * (l) Y (l).
Funções e Vetores
Até agora, os sistemas que estudamos tinham vetores de estados de dimensão finita. Por exemplo, uma rotação simples é descrita por um espaço de estados bidimensional. Por esse motivo, os observáveis tinham apenas um número finito de possíveis valores observáveis. Mas existem observáveis mais complexos que podem ter um número infinito de valores. Um exemplo é uma partícula. As coordenadas de partículas são observáveis, mas, diferentemente da rotação, as coordenadas têm um número infinito de valores possíveis. Por exemplo, uma partícula que se move ao longo do eixo x pode estar em qualquer marca de material x. Em outras palavras, x é uma variável infinita contínua. Quando os sistemas observados são contínuos, a função de onda se torna uma função completa da variável contínua. Para aplicar a mecânica quântica a sistemas desse tipo, precisamos expandir o conceito de vetores para incluir funções nele.
Funções são funções e vetores são vetores; elas parecem ser entidades completamente diferentes; portanto, em que sentido são vetores de funções? Se você pensa em vetores como setas no espaço tridimensional, é claro que eles não são iguais às funções. Mas se você observar os vetores de maneira mais ampla, como nos objetos matemáticos que satisfazem alguns postulados, as funções realmente formam um espaço vetorial. Esse espaço vetorial é chamado de espaço de Hilbert em homenagem ao matemático David Hilbert.
Considere o conjunto de funções complexas Y (x) de uma variável real x. Por uma função complexa, quero dizer que para cada x associa um número complexo Y (x). A variável independente x, por outro lado, é uma variável real comum. Pode levar valores reais de –∞ a + ∞.
Agora, declaramos exatamente o que queremos dizer dizendo que "funções são vetores". Esta não é uma analogia ou metáfora superficial. Sob algumas restrições (às quais retornaremos mais tarde), funções como Y (x) satisfazem os axiomas matemáticos que definem um espaço vetorial. Mencionamos brevemente essa idéia na seção 1.9.2, e agora a usamos com força total. Olhando para os axiomas de um espaço vetorial complexo (na Seção 1.9.1), vemos que funções complexas satisfazem todos eles.
1. A soma de quaisquer duas funções é uma função.
2. A adição de funções é comutativa.
3. A adição de funções é associativa.
4. Existe uma função zero exclusiva, de modo que, quando adicionada a qualquer função, é obtida a mesma função.
5. Para qualquer função Y (x), existe uma função exclusiva –Y (x) tal que Y (x) + (–Y (x)) = 0.
6. A multiplicação de uma função por qualquer número complexo fornece uma função e é linear.
7. A propriedade de distribuição é observada, o que significa que
z [Y (x) + j (x)] = zY (x) + zj (x),
[z + w] Y (x) = zY (x) + wY (x),
onde z e w são números complexos.
Tudo isso implica que podemos identificar a função Y (x) com o vetor ket | Y〉 no espaço vetorial abstrato. Não é de surpreender que também possamos definir vetores de sutiã. O vetor de sutiã 〈Y | correspondente ao chum sal | Y〉 é identificado com a complexa função conjugada Y * (x).
Para usar essa idéia efetivamente, precisamos generalizar alguns objetos do nosso conjunto de ferramentas matemáticas. Nas palestras anteriores, os rótulos que identificavam as funções das ondas eram membros de algum conjunto discreto finito, por exemplo, os valores próprios de um determinado observável. Mas agora a variável independente é contínua. Entre outras coisas, isso significa que não podemos resumir usando valores comuns. Eu acho que você sabe o que fazer. Aqui estão substitutos orientados à função para nossos três conceitos de vetores, dois dos quais você já está familiarizado.
• Os valores são substituídos por integrais.
• Probabilidades são substituídas por densidades de probabilidade.
• O símbolo delta Kronecker é substituído pela função delta Dirac.
Vamos dar uma olhada nessas ferramentas.
Os valores são substituídos por integrais . Se realmente quiséssemos manter o rigor, começaríamos substituindo o eixo x por um conjunto discreto de pontos separados por intervalos muito pequenos ε, e depois passamos para o limite ε → 0. Seriam necessárias várias páginas para justificar cada etapa. Mas podemos evitar esse aborrecimento com algumas definições intuitivas, como substituir somas por integrais. Esquematicamente, essa abordagem pode ser escrita da seguinte maneira:
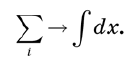
Por exemplo, se você precisar calcular a área sob a curva, o eixo x será dividido em pequenos segmentos, e as áreas de um grande número de retângulos serão somadas, como em uma análise matemática elementar. Quando permitimos que os segmentos se contraiam no tamanho zero, a soma se torna uma integral.
Considere a chave 〈Y | e ket | Y〉 e definem seu produto interno. A maneira óbvia de fazer isso é substituir a soma na equação (1.2) pela integração. Definimos o produto interno da seguinte maneira:
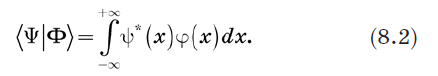Probabilidades são substituídas por densidades de probabilidade . A seguir, identificamos P (x) = Y * (x) Y (x) com a densidade de probabilidade para a variável x. Por que com densidade de probabilidade, e não apenas com probabilidade? Se x é uma variável contínua, a probabilidade de que ele aceite qualquer valor exatamente determinado é geralmente zero. Portanto, é mais correto colocar a questão da seguinte maneira: qual é a probabilidade de que x esteja entre dois valores x = aex = b? A densidade de probabilidade é determinada de modo que essa probabilidade seja dada pela integral
Como a probabilidade total deve ser 1, podemos definir a normalização do vetor como
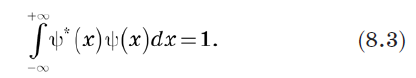O símbolo delta Kronecker é substituído pela função delta Dirac . Até agora, tudo tem sido muito familiar. A função Dirac Delta é algo novo. A função delta é um análogo do símbolo delta do Kronecker dij, que por definição é 0 se i ≠ j e 1 se i = j. Mas isso pode ser definido de outra maneira. Considere qualquer vetor Fi em um espaço de dimensão finita. É fácil ver que o símbolo delta Kronecker satisfaz a condição
Isso se deve ao fato de que apenas termos com j = i são diferentes de zero nesta soma. Durante a soma, o símbolo Kronecker filtra todos os componentes de F, exceto Fi. Uma generalização óbvia disso será definir uma nova função que tenha a mesma propriedade de filtragem quando usada sob a integral. Em outras palavras, precisamos de uma nova entidade d (x - x '), que possua a propriedade que, para qualquer função F (x)
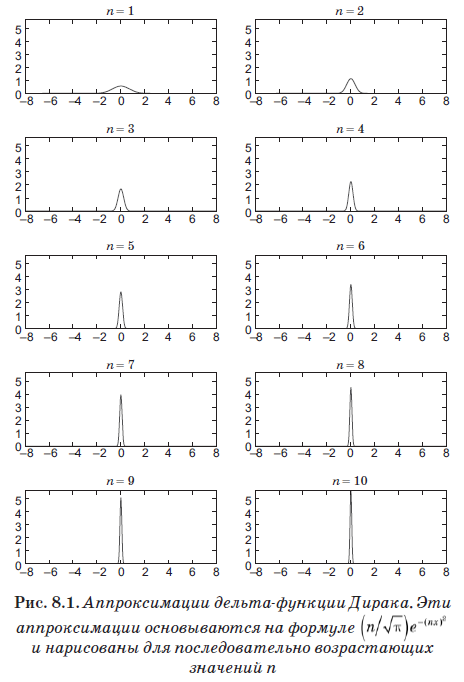
A equação (8.4) define uma nova entidade chamada função delta Dirac, que acabou sendo a ferramenta mais importante na mecânica quântica. Mas, apesar do nome, isso não é realmente uma função no sentido usual. É igual a zero onde x ≠ x ', mas quando x = x' vai para o infinito. De fato, é infinito apenas o suficiente para que a área sob d (x) seja igual a 1. Grosso modo, essa função é diferente de zero no intervalo infinitamente pequeno ε, mas nesse intervalo tem o valor 1 / ε. Assim, a área abaixo é igual a 1 e, mais importante, satisfaz a equação (8.4). Função
aproxima muito bem a função delta para valores muito grandes de n. Na fig. 8.1 mostra essa otimização com valores crescentes de n. Apesar do fato de termos escolhido n = 10, ou seja, um valor muito pequeno, observe que o gráfico já se tornou um pico muito estreito e acentuado.
»Mais informações sobre o livro podem ser encontradas no
site do editor»
Conteúdo»
TrechoPara os leitores deste blog, um desconto de 20% no cupom -
Sasskind