O livro “Teórico mínimo. Tudo o que você precisa saber sobre a física moderna ”

“Mínimo teórico” é um livro para quem perdeu aulas de física na escola e no instituto, mas já se arrepende. Quer entender o básico das ciências naturais e aprender a pensar e raciocinar como os físicos modernos fazem? De forma original e fora do padrão, os famosos cientistas americanos Leonard Sasskind e George Grabowski oferecem um curso introdutório de matemática e física para mentes curiosas.

Ao contrário de outros livros científicos populares que tentam explicar as leis da física de maneira acessível, evitando habilmente equações e fórmulas, os autores ensinam ao leitor os fundamentos clássicos das ciências naturais. O livro oferece sua própria metodologia de ensino original, complementada por palestras em vídeo publicadas em theoryminimum.com .

Aula 9. Fluido de fase e o teorema de Gibbs - Liouville

Lenny gostava de olhar o rio, principalmente de observar as pequenas manchas flutuando na superfície. Ele tentou imaginar como eles iriam se mover entre pedras ou cair em redemoinhos. Mas o curso do rio como um todo - o movimento combinado de um grande volume de água, com correntes que se separam, convergem e se sobrepõem - estava além de sua compreensão.

Fluido de fase

Concentrar-se em condições iniciais específicas e seguir uma trajetória separada no espaço de fases é muito natural para a mecânica clássica. Mas há também uma visão mais ampla que abrange toda uma família de trajetórias. Em vez de colocar a ponta do lápis em um determinado ponto no espaço de fase e seguir o único caminho a partir daí, tentaremos fazer algo mais ambicioso. Imagine que temos um número infinito de lápis e os utilizamos para preencher uniformemente o espaço de fase com pontos (por homogeneidade, quero dizer que a densidade de pontos no espaço q, p é a mesma em todos os lugares). Considere esses pontos como partículas que compõem um fluido imaginário preenchendo o espaço de fase.

Agora, cada ponto se move de acordo com as equações de movimento hamiltonianas:


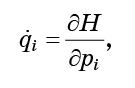
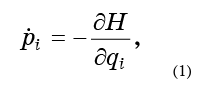
para que nosso fluido flua infinitamente através do espaço de fase.

Um oscilador harmônico é um bom exemplo inicial. Na aula 8, vimos que cada ponto se move em uma órbita circular com uma velocidade angular constante. (Deixe-me lembrá-lo de que estamos falando de fase, não de espaço de coordenadas. Em coordenadas, o oscilador se move para frente e para trás em uma dimensão.) Todo o fluido como um todo faz um movimento sólido, girando uniformemente em torno da origem do espaço de fase.

Agora, de volta ao caso geral. Se o número de coordenadas for N, o espaço de fase e o líquido nele serão bidimensionais. O fluido flui, mas de uma maneira muito específica. Seu fluxo tem propriedades especiais. Uma delas é que, se um ponto começa com uma certa energia - ou seja, para um determinado valor de H (q, p) -, ele armazena esse valor de energia. As superfícies de energia constante (por exemplo, com energia igual a E) são determinadas pela equação H (q, p) = E. (2)

Para cada valor de E, temos uma equação com variáveis ​​de espaço de fase 2N que define uma superfície da dimensão 2N - 1. Em outras palavras, cada valor de E tem sua própria superfície; quando você ultrapassa todos os valores E, essas superfícies preenchem todo o espaço da fase. Podemos considerar o espaço de fase com as superfícies dadas pela equação (2) como um mapa de contornos (Fig. 1), no qual as horizontais representam não a altura, mas os valores de energia. Se o ponto líquido estiver em uma superfície específica, ele permanecerá para sempre. Esta é a lei da conservação de energia.

O espaço de fase do oscilador harmônico é bidimensional e as superfícies de energia são círculos:

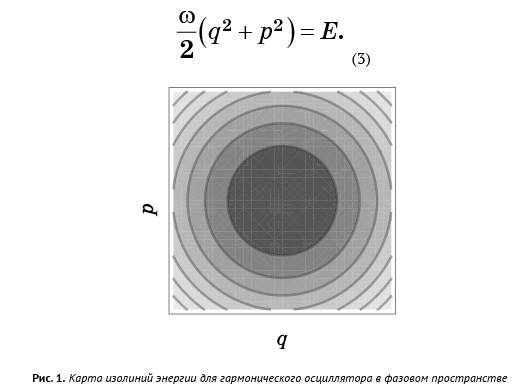
No caso geral, as superfícies de energia de um sistema mecânico são muito complicadas para serem visualizadas, mas o princípio permanece o mesmo: as superfícies de energia preenchem o espaço da fase como camadas e o fluxo se move para que os pontos permaneçam na superfície em que estavam originalmente .

Lembrete breve

Gostaria de parar por aqui e relembrar o que foi dito na primeira palestra, onde foram discutidas moedas, dados e as idéias mais simples sobre as leis do movimento. Descrevemos essas leis com um conjunto de setas conectando os pontos que representam os estados do sistema. Também explicamos que as leis são admissíveis e inadmissíveis, enquanto as admissíveis são reversíveis. A conclusão é que cada ponto deve ter exatamente uma seta de entrada e exatamente uma seta de saída. Se pelo menos em um ponto o número de setas recebidas exceder o número de saídas (isso é chamado de convergência), essa lei é irreversível. O mesmo se aplica ao caso em que existem mais setas de saída do que as de entrada (isso é chamado de divergência). A divergência e a convergência de flechas violam a reversibilidade e são proibidas. Até agora, não retornamos a essa linha de raciocínio. Agora chegou a hora.

Fluxo e divergência

Considere alguns exemplos simples de fluxo de fluido no espaço comum. Por um momento, esquecemos o espaço de fase e consideramos um fluido comum movendo-se no espaço tridimensional usual, com eixos indicados como x, y, z. O fluxo pode ser descrito pelo campo de velocidade . Campo velocidade

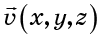
é determinado pela configuração do vetor de velocidade em cada ponto no espaço (Fig. 2).

Você também pode descrever o campo de velocidade com componentes de velocidade:

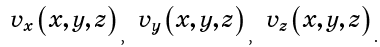
Além disso, a velocidade em um ponto pode depender do tempo, mas vamos supor que não exista essa dependência. Nesse caso, o fluxo é chamado estacionário .

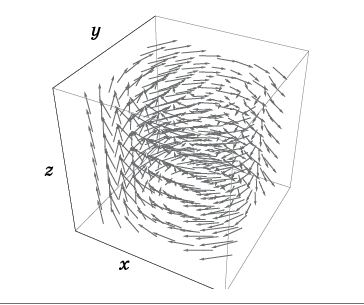
Fig. 2. Campo de velocidade

leva a mesma quantidade. Isso também significa que a densidade de um fluido - o número de moléculas por unidade de volume - é a mesma em todos os lugares e é constante ao longo do tempo. A propósito, o termo "incompressibilidade" também significa inextensibilidade. Em outras palavras, o líquido não pode aumentar de volume. Considere uma pequena célula cúbica definida pelas condições:

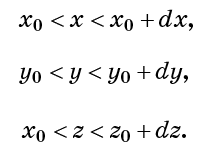
Incompressibilidade implica que o número de pontos de fluido em cada célula seja constante. Isso também significa que o fluxo total de fluido que entra na célula (por unidade de tempo) deve ser zero. (Quantos pontos do fluxo entram, o mesmo número sai.) Considere o número de moléculas que passam por unidade de tempo através da superfície da célula x = x0. Será proporcional à velocidade do fluxo nessa superfície vx (x0).

Se a velocidade vx for a mesma em x0 e em x0 + dx, o fluxo na célula através de x = x0 será o mesmo que o fluxo da mesma através de x = x0 + dx. Mas se vx mudar em toda a célula, esses dois fluxos serão desequilibrados. O fluxo total entrando na célula através dessas duas faces será proporcional

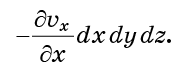
Exatamente as mesmas considerações se aplicam às faces y0 e y0 + dy, bem como z0 e z0 + dz. Se todas elas forem adicionadas, o fluxo total de moléculas para a célula (entrada menos saída)

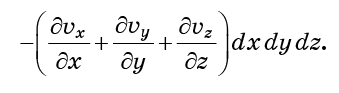
A combinação de derivadas entre parênteses é chamada de divergência do campo vetorial
e é designado

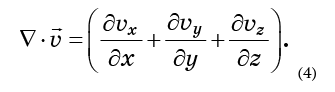
A divergência reflete o grau de dispersão das moléculas ou o aumento do volume ocupado por elas. Se o fluido for incompressível, esse volume não deve mudar, o que significa que a divergência deve ser zero.

Uma maneira de entender a incompressibilidade é imaginar cada molécula ou ponto como ocupando um volume que não pode ser alterado. Eles não podem ser compactados em um volume menor, não desaparecem e não aparecem do nada. Com um pouco de reflexão, você pode ver como incompressível e reversível são semelhantes. Nos exemplos que analisamos na aula 1, as setas também determinaram um tipo de fluxo. E essencialmente esse fluxo era incompressível, pelo menos se fosse reversível. A questão natural que se segue é: o fluxo no espaço de fase é reversível? A resposta é sim, se o sistema atender às equações de Hamilton. E o teorema que expressa essa incompressibilidade é chamado teorema de Liouville.

Teorema de Liouville

Vamos retornar ao fluxo de fluido no espaço de fase e considerar os componentes da velocidade do fluido em cada ponto no espaço de fase. Não é necessário dizer que o fluido da fase não é tridimensional nas coordenadas x, y, z. É um fluido bidimensional nas coordenadas pi, qi.

Assim, existem 2N componentes do campo de velocidade - um para cada coordenada q e cada coordenada p. Deixe eles

O conceito de divergência expresso pela equação (4) é facilmente generalizado para qualquer número de dimensões. Em três dimensões, essa é a soma das derivadas dos componentes de velocidade nas direções correspondentes. Da mesma maneira, é determinado para qualquer número de dimensões. No caso do espaço de fase, a divergência do fluxo é a soma dos 2N membros:

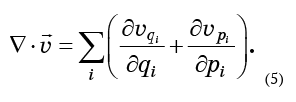
Se o fluido for incompressível, essa expressão deverá ser zero. Para calcular, você precisa conhecer os componentes do campo de velocidade - eles, é claro, nada mais são do que as velocidades das partículas do fluido da fase.

O vetor de fluxo em um determinado ponto é identificado com a velocidade de uma partícula imaginária naquele ponto. Em outras palavras

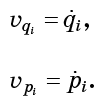
Além disso,
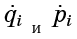
- estas são apenas as quantidades que entram nas equações de Hamilton (1):


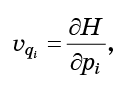
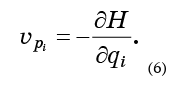
Tudo o que precisa ser feito é substituir as equações (6) na fórmula (5) e obter

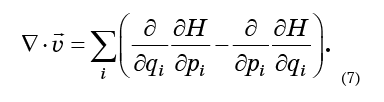
Lembrando que a segunda derivada do formulário


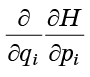
não depende da ordem de diferenciação, entenderemos que os termos da equação (7) se destroem exatamente em pares:


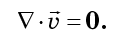
Portanto, o fluido da fase é incompressível. Na mecânica clássica, a incompressibilidade de um fluido de fase é chamada de teorema de Liouville, embora quase não tenha relação com o matemático francês Joseph Liouville. Foi publicado pela primeira vez em 1903 pelo grande físico americano Josiah Willard Gibbs, e também é conhecido como o teorema de Gibbs - Liouville.

Determinamos a incompressibilidade de um fluido exigindo que a quantidade total de fluido que entra em qualquer célula pequena seja zero. Há outra definição estritamente equivalente. Imagine um volume de líquido em algum momento. Esse volume pode ter qualquer formato: esférico, cúbico, em forma de gota - qualquer que seja. Agora vamos acompanhar o movimento de todos os pontos deste volume. Depois de algum tempo, uma gota de líquido estará em um local diferente e terá uma forma diferente. Mas se o fluido for incompressível, o volume da gota permanecerá o mesmo que era originalmente. Assim, podemos reformular o teorema de Liouville: o volume ocupado por uma gota de líquido de fase é preservado no tempo .

Considere um exemplo de um oscilador harmônico no qual um fluido gira em torno de um ponto de referência. Obviamente, a queda retém o volume, pois todo o seu movimento é reduzido à rotação no estado sólido. O formato da gota permanece inalterado, mas é o caso do oscilador harmônico. Considere outro exemplo. Suponha que o hamiltoniano tenha a forma H = pq.

Talvez isso lhe pareça diferente do Hamiltoniano, embora esteja completamente correto. Derivamos as equações de movimento:

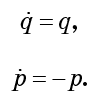
De acordo com essas equações, q aumenta exponencialmente com o tempo ep diminui exponencialmente com a mesma velocidade. Em outras palavras, o fluxo pressiona o fluido contra o eixo p, enquanto simultaneamente o expande ao longo do eixo q na mesma extensão. Qualquer queda se estende ao longo de q e se contrai ao longo da p. Obviamente, a queda experimenta tremendas deformações, mas seu volume de fase não muda.

O teorema de Liouville é o análogo mais próximo imaginável do tipo de irreversibilidade que discutimos na aula 1. Na mecânica quântica, o teorema de Liouville é substituído por uma versão quântica chamada unitariedade. A unitariedade é ainda mais parecida com o que discutimos na aula 1, mas este é o tópico da próxima edição de O mínimo teórico.

»Mais informações sobre o livro podem ser encontradas no site do editor
» Exclamação
» Trecho

Para os leitores deste blog, um desconto de 20% no cupom - mínimo teórico