Tendo derramado areia sobre uma placa elástica oscilante, pode-se ver a formação das figuras de Hladni . Eles costumam servir como um exemplo da "beleza natural" dos fenômenos físicos, embora por trás deles esteja a física bastante simples da excitação ressonante das ondas estacionárias. E poucas pessoas prestam atenção à característica curiosa dessas figuras: as linhas nelas evitam interseções, como se alguma força as repelisse. Vamos tentar entender que tipo de física está oculta por trás dessa repulsão e como ela está relacionada à teoria quântica do caos.

Ondas estacionárias

Como sabemos, os corpos elásticos podem produzir vibrações bastante complexas, durante as quais se contraem, esticam, dobram e torcem. No entanto, as vibrações de qualquer corpo elástico podem ser representadas como uma combinação de vibrações normais mais simples, sobrepostas umas às outras. É assim que várias vibrações normais de um corpo elástico simples - uma corda esticada unidimensional - se parecem.

Cada oscilação normal é representada por uma onda estacionária , que, diferentemente de uma onda itinerante, fica parada e possui seu próprio padrão de distribuição das amplitudes das oscilações no espaço. Nesta figura, antinodos podem ser distinguidos - pontos onde a amplitude das oscilações atinge o máximo, e nós - pontos fixos em que a amplitude das oscilações é zero. Além disso, cada uma dessas ondas oscila com sua própria frequência . No caso de uma corda, como você pode ver, a frequência de oscilações de uma onda estacionária aumenta com o aumento do número de nós e antinodos.


Vejamos agora um sistema bidimensional, um exemplo do qual é uma fina membrana elástica esticada sobre uma estrutura rígida. As vibrações normais de uma membrana redonda parecem mais complicadas do que no caso de uma corda e, em vez de nós de pontos individuais, existem linhas nodais ao longo das quais a membrana está estacionária.


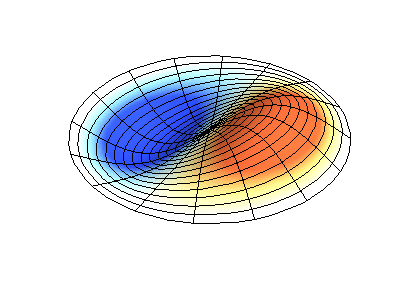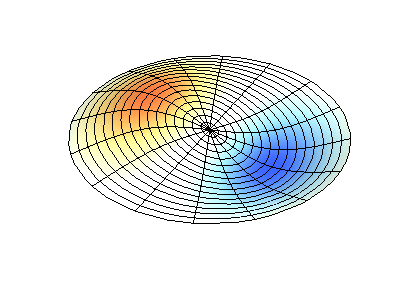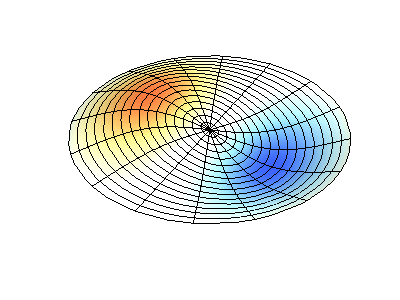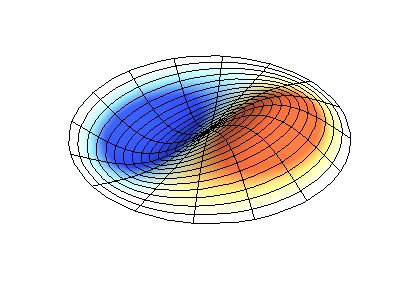
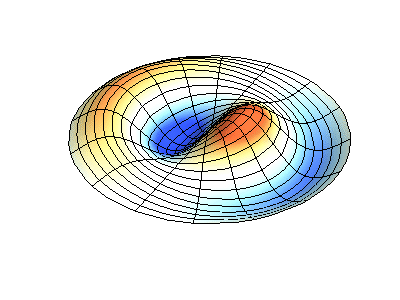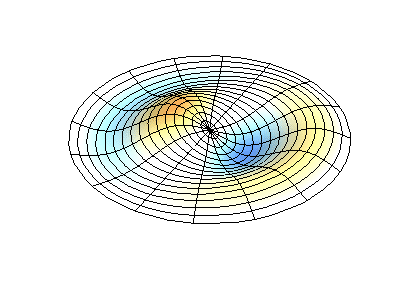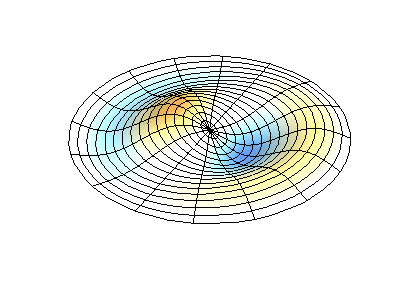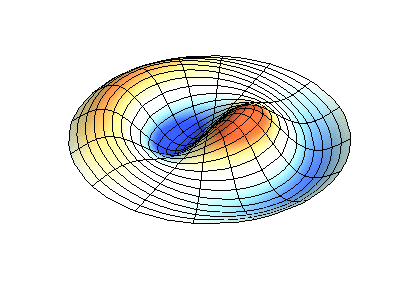
Vibrações normais de uma membrana redonda com bordas fixas. Fonte


A cor verde mostra linhas nodais.

Em uma membrana redonda, as linhas nodais, que são círculos e segmentos ao longo dos raios, podem se cruzar em ângulos retos. Se as bordas da membrana tiverem uma forma arbitrária, encontrar as frequências de vibrações e padrões normais de seus nós e antinodos se transformará em um problema que só pode ser resolvido usando um computador.

Perfis da amplitude de oscilações de ondas estacionárias em membranas na forma de um quadrado com um buraco , flocos de neve Koch e a superfície de um gatinho .

As equações que descrevem as oscilações de uma placa elástica fina diferem das equações de oscilação da membrana, uma vez que a placa possui rigidez própria, enquanto a membrana é macia e flexível apenas devido à tensão por forças externas. No entanto, também existem conjuntos de vibrações normais, cujos desenhos dependem substancialmente da forma dos limites.

Figuras de Hladni

Como mencionado acima, no caso geral, as vibrações corporais são uma combinação de todo um conjunto de vibrações normais excitadas nele. O fenômeno da ressonância permite excitar seletivamente uma das vibrações normais de que precisamos - para isso, precisamos balançar o corpo usando uma força externa com uma frequência igual à frequência natural da oscilação normal.

Os dois vídeos abaixo mostram um esquema típico para obter figuras de Hladni: uma placa elástica é presa no centro a um gerador de vibrações mecânicas, cuja frequência aumenta gradualmente. As vibrações normais da placa com seus padrões de nós e antinodos são excitadas quando a frequência do oscilador corresponde ressonantemente às frequências naturais dessas vibrações (as frequências naturais são mostradas no vídeo no canto inferior esquerdo).

Aqui está a versão do mesmo vídeo em que as frequências de vibrações normais podem ser estimadas pelo ouvido.

E aqui está um pouco mais bonito.

Vemos padrões de nós e antinodos devido ao fato de que as correntes de ar próximas a uma placa oscilante sopram grãos de areia nas linhas nodais de uma onda estacionária ^(*) Assim, as figuras de Hladni nos mostram padrões de linhas nodais de vibrações normais de uma placa elástica.

Várias figuras de Hladni no convés superior do violão. Fonte

Outro exemplo de ondas normais são as ondas estacionárias na superfície da água. Eles são descritos por uma equação que difere das equações de vibração das placas e membranas, mas segue as mesmas leis qualitativas e, com sua ajuda, é possível obter análogos das figuras de Hladni.

Micropartículas na superfície da água em vasos de várias formas. A linha preta mostra uma escala de 2 milímetros. Fonte

Caos clássico

Então, vimos que, no caso de uma membrana redonda, as linhas nodais são teoricamente! - cruzam notavelmente, ao mesmo tempo, nas figuras de Hladni em placas quadradas ou mais complexas, as linhas nodais evitam interseções. Para entender a razão desses padrões, teremos de fazer uma pequena excursão à teoria do caos.

O caos clássico é uma propriedade dos sistemas mecânicos, consistindo em uma dependência extremamente forte da trajetória de seus movimentos das mudanças nas condições iniciais. Essa relação também é conhecida como " efeito borboleta ". Um exemplo vívido de comportamento caótico pode ser encontrado nas tentativas de prever o clima: o sistema de equações que descreve o movimento da atmosfera e dos oceanos não permite que sejam feitas previsões suficientemente precisas a longo prazo devido a erros exponencialmente crescentes devido a pequenas imprecisões nos dados iniciais ^(**)

O fenômeno do caos foi abertamente popularizado pelo meteorologista e matemático Edward Lorenz , que descobriu que dois cálculos de previsão do tempo começando com condições iniciais muito próximas eram inicialmente quase indistinguíveis, mas em algum momento eles começaram a divergir radicalmente.

Dois cálculos de Edward Lorenz, a partir dos valores iniciais próximos 0,506 e 0,506127. Fonte

Os sistemas mais simples, nos quais é conveniente estudar o caos, são os de bilhar - seções de uma superfície plana ao longo da qual uma bola pode rolar sem atrito, batendo absolutamente elástico nas paredes rígidas. Nos bilhares caóticos, as trajetórias da bola, que apresentam pequenas diferenças no início, divergem significativamente posteriormente. Um exemplo de bilhar caótico é o bilhar do Sinai mostrado abaixo, que é uma piscina retangular com um obstáculo circular no centro. Como veremos, é justamente por esse obstáculo que o bilhar se torna caótico.

Duas trajetórias de bola exponencialmente divergentes nos bilhares do Sinai. Fonte

Sistemas integráveis ​​e caóticos

Sistemas mecânicos que não são caóticos são chamados integráveis e, com o exemplo de bilhar, você pode ver claramente a diferença entre sistemas integráveis ​​e caóticos.

Bilhar retangular e redondo são integráveis ​​devido à sua forma simétrica ^(***) O movimento da bola nesses bilhar é simplesmente uma combinação de dois movimentos periódicos independentes. No bilhar retangular, esses são movimentos com saltos das paredes na horizontal e na vertical, e circularmente esse é o movimento ao longo do raio e o movimento angular em um círculo ao redor do centro. Esse movimento é facilmente calculado e não mostra comportamento caótico.

Trajetórias de bola em bilhar integrável.

Bilhar de forma mais complexa, que não possui uma simetria tão alta quanto um círculo ou retângulo, é caótico ^(****) Um deles que vimos acima são os bilhares do Sinai, nos quais a simetria do retângulo é destruída por uma inclusão circular no centro. Também são frequentemente considerados "estádio" de bilhar e bilhar na forma de caracóis Pascal. A bola se move em bilhar caótico por caminhos muito complicados e não se decompõe em movimentos periódicos mais simples.

A trajetória da bola no caótico "estádio" e "caracol Pascal".

Aqui você já pode adivinhar que a presença de interseções entre as linhas nas figuras de Hladni é determinada pelo fato de a placa ter a forma de um bilhar integrável ou caótico. Isso é claramente visto nas fotos abaixo.

Placas redondas Hladni, demonstrando as propriedades dos bilhares integrados. Fonte

Demonstrando as propriedades dos caóticos bilhares do prato Hladni na forma de “estádio” de bilhar, o caso do violino e da praça, cuja simetria é quebrada por uma luminária redonda no centro (análogo dos bilhares do Sinai). Fonte

Caos quântico

Como entender por que as interseções entre linhas nodais se devem à integrabilidade dos bilhares? Para fazer isso, precisamos nos voltar para a teoria quântica do caos , combinando a teoria do caos com a mecânica das oscilações e ondas. Se na mecânica clássica a bola no bilhar é descrita como um ponto material que se move ao longo de uma determinada trajetória, na mecânica quântica seu movimento é descrito como a propagação de uma onda que obedece à equação de Schrödinger e refletida nas paredes do bilhar.

Estágios da propagação de ondas em bilhar quântico. Inicialmente, a onda é concentrada em um pulso redondo e se move da esquerda para a direita, depois se espalha e reflete repetidamente nas paredes. Fonte

O mesmo na forma de animação, mas com condições iniciais ligeiramente diferentes.

Como no caso de vibrações de membranas e placas, a equação de Schrödinger que descreve bilhar quântico permite encontrar vibrações normais na forma de ondas estacionárias, que têm um padrão característico de linhas nodais e antinodos, individuais para cada oscilação e dependendo da forma dos limites.

Exemplos de perfis das amplitudes de oscilações em ondas estacionárias em bilhar quântico caótico “ caracol de Pascal ” e “ estádio ”.

Os padrões das ondas estacionárias nos bilhares quânticos integráveis ​​e caóticos são qualitativamente diferentes: os bilhares integráveis ​​mostram padrões ordenados simétricos das ondas estacionárias, enquanto nos bilhares caóticos os padrões das ondas estacionárias são muito confusos e não mostram nenhum padrão visível (no final do artigo, será mostrado que alguns padrões ainda existem).

As amplitudes de oscilação nas ondas estacionárias de um bilhar redondo integrável (linha superior) e bilhar caótico na forma de um caracol Pascal (linha inferior). Fonte

As imagens bizarras de vibrações normais em bilhar caótico às vezes servem como objeto de um estudo separado. Fonte

Uma diferença qualitativa também é vista nos padrões das linhas nodais: no caso de bilhar quântico integrável, vemos famílias ordenadas de linhas que se cruzam mutuamente e, no bilhar caótico, essas linhas, em regra, não se cruzam .

Acima: linhas nodais (linhas pretas entre áreas azuis e vermelhas) de ondas estacionárias de bilhar integrável - redondo e retangular -. Abaixo: as linhas nodais de uma das ondas estacionárias nos caóticos bilhar - um quarto dos bilhares do estádio .

Interseção ou não interseção?

Por que as linhas nodais no bilhar caótico não se cruzam? Em 1976, a matemática Karen Uhlenbeck provou um teorema segundo o qual as linhas nodais de ondas estacionárias de bilhar quântico, em geral, não deveriam se cruzar.

De uma forma simplificada, isso pode ser mostrado da seguinte forma: suponha que duas linhas nodais se cruzem em um ponto ( x ₀ , y ₀ ). Para que isso aconteça, a função f ( x, y ), que determina a dependência da amplitude da onda estacionária nas coordenadas, deve simultaneamente satisfazer três condições:

1) Deve ser igual a zero no ponto ( x ₀ , y ₀ ), pois esse ponto é nodal.
2) Se você se mover do ponto ( x ₀ , y ₀ ) na direção da primeira linha nodal, f ( x, y ) deverá permanecer igual a zero.
3) Se você se mover do ponto ( x ₀ , y ₀ ) na direção da segunda linha nodal, f ( x, y ) também deverá permanecer igual a zero.


No total, temos três condições (ou três equações) impostas à função de duas variáveis f ( x, y ). Como sabemos, uma equação não é suficiente para encontrar completamente as duas incógnitas xey , duas equações já são suficientes para isso e três equações são demais. O sistema de três equações para duas incógnitas, de um modo geral, não terá soluções, a menos que tenhamos sorte. Portanto, os pontos de interseção das linhas nodais podem existir apenas como uma exceção .

Nos bilhares integráveis, essas exceções simplesmente surgem. Como vimos acima, suas propriedades especiais - previsibilidade de movimento, ausência de caos, padrões regulares de ondas estacionárias - são o resultado de sua alta simetria. A mesma simetria garante o cumprimento simultâneo de três condições necessárias para interseções de linhas nodais.

Vamos agora examinar mais de perto exemplos de figuras de Hladni típicas de bilhar integrável e caótico. A figura abaixo mostra três casos característicos . À esquerda, a placa tem a forma de um círculo, de modo que o bilhar quântico correspondente é integrável e as linhas nodais se cruzam. No centro, a placa é retangular, o que também corresponde a um sistema integrável; no entanto, a montagem redonda no centro viola levemente a simetria do retângulo, de modo que as linhas nodais não se cruzam em todos os lugares. Um exemplo de um sistema puramente caótico é mostrado à direita: uma placa no formato de um quarto dos bilhares do Sinai (no canto superior direito há um recorte circular), as linhas nodais nas quais não mais se cruzam.



Assim, quanto mais forte a forma da placa - levando em consideração a sua fixação - difere da forma de um bilhar integrado (como um círculo ou retângulo), menos intersecções de linhas nodais nela .

Não é tão fácil obter figuras bonitas de Hladni com linhas que se cruzam em um prato redondo. Quando vibrações emocionantes com uma fixação central, a simetria circular de todo o sistema proíbe a formação de linhas nodais radiais; portanto, veremos apenas um conjunto chato de círculos (essa dificuldade pode ser contornada por vibrações emocionantes, não do centro, mas da borda da placa usando o arco do violino). Se a placa for fixada descentralizada, os números de Hladni se tornarão mais interessantes, mas devido à violação da simetria circular, o sistema deixará de ser integrável.

Placa redonda, montagem central.

Prato redondo, montagem deslocada do centro.

E aqui estão opções diferentes com placas redondas e não circulares.

Por fim, um leitor atento pode perceber: mas vejo que às vezes as linhas nodais se cruzam mesmo em pratos “caóticos”. Como é que se a interseção é proibida pelo teorema de Uhlenbeck?

Em primeiro lugar, as linhas nodais podem evitar a interseção, mas antes elas se aproximam tanto que, devido à largura finita do caminho da areia, parecer-nos-á que existe uma interseção. Em segundo lugar, entre sistemas integráveis ​​e caóticos, de fato, não há limites nítidos.

Linhas nodais - separam áreas em preto e branco - em bilhar quântico integrável e caótico (esquerdo e direito), e no caso pseudo-integrável intermediário (no centro). No caso intermediário, existem várias interseções das linhas nodais, enquanto no caso caótico não há nenhuma. Fonte

Na teoria clássica do caos, a famosa teoria de Kolmogorov-Arnold-Moser é dedicada a essa questão. Ela diz que se a simetria do sistema integrável for levemente violada, ele não exibirá imediatamente um comportamento caótico, mas, na maioria das vezes, manterá sua previsibilidade de movimento. No nível da teoria quântica do caos e das figuras de Hladni, isso se manifesta no fato de que em alguns lugares as intersecções das linhas nodais são preservadas. Isso ocorre em pontos particularmente simétricos do bilhar ou longe da fonte de perturbação, o que viola a simetria do sistema integrável.

O que mais?

O que mais é interessante na teoria quântica do caos? Para o leitor interessado, mencionarei três perguntas adicionais que não estão mais diretamente relacionadas às figuras de Hladni.

1) Um fenômeno importante estudado por essa teoria é a universalidade dos sistemas caóticos. A grande maioria dos sistemas em que as vibrações normais podem ocorrer são caóticos, e todos eles - independentemente de sua natureza física! - obedeça às mesmas leis. O fenômeno da universalidade, no qual sistemas completamente diferentes são descritos pelas mesmas fórmulas, é muito bonito e serve como um lembrete da unidade matemática do mundo físico.

Estatísticas de distâncias entre frequências adjacentes de vibrações normais em sistemas caóticos de diferentes naturezas físicas, descritas em todos os lugares pela mesma fórmula universal de Wigner-Dyson. Fonte

2) Os padrões de vibrações normais de bilhar caótico têm uma característica interessante chamada “cicatrizes quânticas” . Vimos que os caminhos da bola no bilhar caótico costumam parecer muito confusos. Mas há exceções - são órbitas periódicas , trajetórias fechadas bastante simples e curtas ao longo das quais a bola faz movimentos periódicos. As cicatrizes quânticas são chamadas de espessamento acentuado das ondas estacionárias ao longo de órbitas periódicas.

Cicatrizes quânticas no "estádio" de bilhar, percorrendo as órbitas periódicas mostradas pelas linhas vermelha e verde. Fonte

3) Até agora, falamos sobre sistemas bidimensionais. Se considerarmos a propagação de ondas no espaço tridimensional, também poderão surgir linhas nodais ao longo das quais a amplitude da oscilação é zero. Isso é especialmente importante ao estudar a condensação e a superfluidez de Bose, onde milhares de átomos se movem como " ondas de matéria " únicas. É necessária uma análise da estrutura das linhas nodais de ondas de matéria no espaço tridimensional, por exemplo, para entender como a turbulência quântica surge e se desenvolve em sistemas superfluídos.

Estruturas tridimensionais emaranhadas de linhas nodais de "ondas de matéria" estacionárias no condensado de Bose. Fonte .

^(*) Se o tamanho das partículas derramadas sobre a placa for pequeno o suficiente, elas serão sopradas não para os nós, mas para os antinodos da onda estacionária, como foi mostrado neste trabalho experimental .

^(**) «» «» , : – , , . .

^(***) – . , , , .

^(****) , – . , . – .