Simetrias C, P, T (e suas combinações)

No século 20, especialistas em física de partículas descobriram que é muito importante levar em consideração todas as simetrias possíveis que podem ser demonstradas pelas leis da natureza que governam as partículas elementares. A presença ou ausência de simetria pode nos revelar aspectos da natureza que, de outra forma, não são óbvios.

Das muitas simetrias possíveis, três podem desempenhar um papel único: conjugação de carga (C), paridade espacial (P) e simetria em relação à reversão do tempo (T). Três dessas transformações, afetando partículas, espaço e tempo, incluem:

• C: substituindo todas as partículas por partículas com carga oposta (carga elétrica e cargas menos familiares; até algumas partículas neutras são substituídas. Por exemplo, os neutrinos mudam para antineutrinos e os nêutrons para antineutrons).
• P: colocando o mundo em um espelho (mais precisamente, alterando a orientação de três dimensões para o oposto).
• T: lançar o mundo na direção oposta do tempo (mais precisamente, mudar a direção da evolução temporal).

Cada uma dessas transformações tem a propriedade de que, se você a realizar duas vezes, retornará ao estado original. No jargão, dizemos que P ² = P × P = 1 (ou seja, se você colocar um espelho em um espelho, o que você vê será o mesmo que se não houvesse espelhos) e, da mesma forma, C ² = 1 e T2 = 1.

Além disso, você pode realizar duas conversões juntos. Por exemplo, você pode criar C e depois P, que simplesmente escrevemos como “CP” (ou você pode criar PC, será o mesmo - a ordem não importa para essas transformações), na qual você coloca o mundo no espelho e muda cargas de partículas. Você pode considerar CT, PT e até CPT. Assim como C, P e T, qualquer uma dessas combinações, quando feita duas vezes, retornará tudo como estava.

E o que fazemos com essas transformações? Precisamos fazer uma pergunta: se imaginarmos um mundo criado a partir do nosso usando uma das transformações, as leis da natureza nele, que governam partículas e interações elementares, funcionarão da mesma maneira que no nosso?

Se a resposta for sim, tudo o que pode acontecer em um mundo novo e transformado pode acontecer no nosso; neste caso, dizemos que essa transformação é a simetria do nosso mundo. Mais precisamente, esta é a simetria das leis da natureza do nosso mundo. Caso contrário, a transformação ainda pode ser realizada, mas não será a simetria do nosso mundo, porque o mundo obtido após a transformação será diferente do nosso.


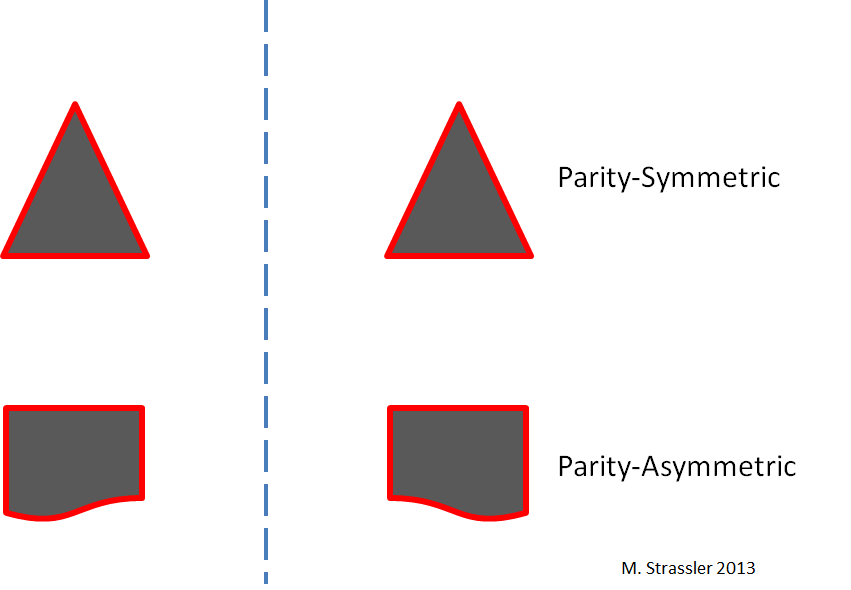Fig. 1

É bastante fácil entender como funciona a paridade espacial (P). Um objeto em particular pode ou não ter simetria de paridade. Como mostrado na fig. 1, o reflexo de um triângulo no espelho nos dá um triângulo idêntico ao primeiro, de modo que o triângulo será simétrico em paridade. Mas uma forma mais complexa, mostrada na parte inferior da fig. 1, não parece exatamente o mesmo após a reflexão, portanto, é assimétrico em paridade.

Obviamente, nosso mundo não é simétrico no espelho; isso pode ser visto em qualquer fotografia da natureza (veja a Fig. 2). No entanto, é necessário distinguir entre a simetria do objeto e a simetria das leis da natureza que governam todos os objetos possíveis. Os processos básicos da física de partículas podem ser simétricos, o que significaria que, para qualquer processo que possa ocorrer na natureza, existe um processo de espelho que também pode ocorrer (Fig. 2, abaixo).

Mas acontece que os processos básicos da natureza não são simétricos em P!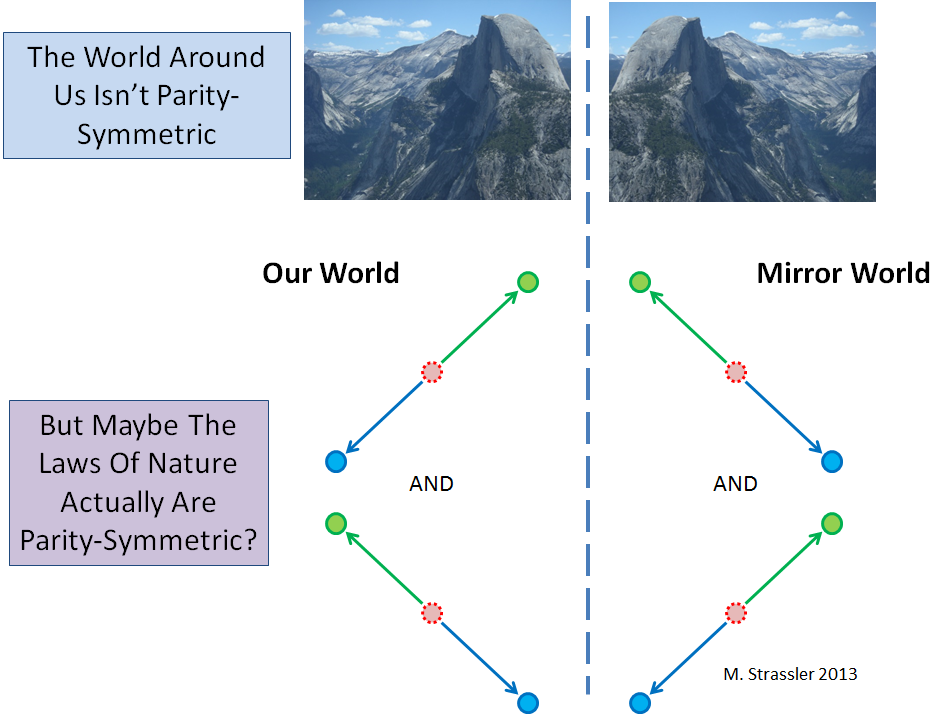


Fig. 2

Um fato marcante é que nem C, nem P, nem T, nem CP, nem CT, nem PC são simetrias da natureza. Os principais processos conhecidos pela física antes do século XX - em particular, incluindo interações gravitacionais e eletromagnéticas, ou seja, todos aqueles que mantêm a Terra unida e mantêm sua órbita ao redor do Sol, e aqueles que controlam a física de átomos e moléculas e toda a química - são simétricos. S, P e T. Os físicos ficaram bastante surpresos quando, nas décadas de 1950 e 1960, descobriram que a interação nuclear fraca rompe todas essas simetrias. A única transformação que ainda é considerada (por boas razões) simétrica à natureza é a CPT.

Observe que, se a CPT for simétrica, os efeitos da CP e T devem ser os mesmos. Como isso é simetria, a aplicação da transformação CPT o leva de volta ao mesmo mundo em que você começou, mas também é sabido que se você aplicar a transformação T duas vezes, retornará ao mesmo mundo em que começou - o que significa que a CP deve fazer o mesmo que produz T. O mesmo vale para os pares CT e P, e para RT e C.

O CPT transforma partículas e suas interações em nosso mundo em antipartículas e suas interações em um mundo transformado e vice-versa. E, como em nosso mundo, cada tipo de partícula possui uma antipartícula (acontece que ela mesma é) e, como cada interação de partículas diferentes tem uma interação com antipartículas (por assim dizer), acredita-se que isso seja perfeitamente simétrico. Mais precisamente, para qualquer mundo cujas partículas obedeçam à teoria quântica de campos, a matemática usada nas equações do Modelo Padrão, que descreve todas as partículas e interações conhecidas, pode-se provar que CPT é simetria. (Isso é verdade para uma teoria unificadora, como a teoria das cordas, que combina a teoria quântica da gravidade com forças não gravitacionais, é difícil dizer; mas as violações da CPT ainda não foram obtidas em experimentos).

C e P não são simetrias devido à fraca interação nuclear

Até a década de 1950, tudo o que os físicos sabiam - toda química e física atômica, todos os efeitos da gravidade e da interação eletromagnética, ondas de luz e os fundamentos do núcleo atômico - correspondiam a um mundo simétrico em P. Mas acontece que C e P não são quase simétricas leis da natureza. Eles são perturbados o mais rápido possível por fracas interações nucleares.


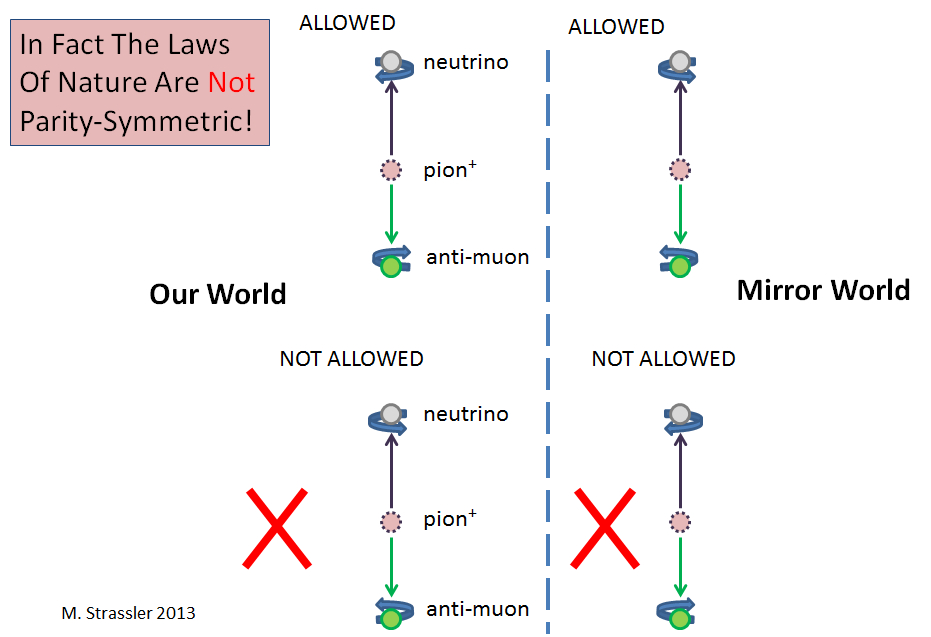Fig. 3

No exemplo mais simples (mas não o único), os neutrinos estão envolvidos. Quando um neutrino aparece em um processo físico, ele é sempre criado usando uma interação nuclear fraca. E quando ocorre, ele sempre gira no sentido anti-horário do ponto de vista do observador localizado no ponto de onde ele está vindo. (Neutrinos, como elétrons e prótons e muitas outras partículas, em certo sentido sempre giram; mais precisamente, eles sempre têm um torque). Em outras palavras, ele gira como um parafuso canhoto (Fig. 3). (No jargão, ele terá um helicóptero negativo). Mas o neutrino produzido pela fraca interação nuclear nunca gira como um parafuso destro. Como P trocaria de lugares destros e canhotos (como em um espelho), isso significa que uma interação nuclear fraca viola R.

Em um exemplo mais específico (Fig. 3), quando um pion carregado positivamente (um hadrão consistindo de um quark superior, um quark anti-baixo e muitos glúons e pares de quark / antiquark) decai em um antimuon e um neutrino, o neutrino é sempre canhoto e nunca destro. Isso viola R. E quando um pion carregado de forma negativa decai em um múon e um antineutrino, o antineutrino é sempre destro. Essa diferença de processos, incluindo peônias com carga negativa e positiva, viola C.

A violação de P e C deste tipo é agora bastante compreensível. O Modelo Padrão (as equações que usamos para descrever todas as partículas e interações conhecidas) inclui-o de uma maneira bastante natural, e os detalhes das equações foram cuidadosamente verificados em experimentos. Portanto, embora as violações de P e C tenham sido uma grande surpresa na década de 1950, hoje elas fazem parte da física de partículas.

No entanto, se olharmos para as próprias partículas (e não entrarmos nos detalhes de suas interações), SR (o mesmo que RS) à primeira vista parece simétrico. Isso ocorre porque P gira o giro do neutrino da esquerda para a direita, mas C inverte a carga pioneira, transforma o antimuon em um múon e substitui o neutrino por um antineutrino; o processo final ocorre em nosso mundo (Fig. 4). Então, por algum tempo, os físicos acreditavam que a interação nuclear fraca preservaria a RS, embora individualmente viole C e R.

Outra maneira de ver isso é ler meu artigo sobre como as partículas ficariam se o campo de Higgs fosse zero. Pode-se ver que, por exemplo, as partículas elétron-esquerda e neutrino-esquerda estão emparelhadas e estão sujeitas à ação de interação fraca de isospina, e a partícula elétron-direita é separada da neutrino-direita e nenhuma delas é sujeita a interação fraca de isospina. Além disso, o que é verdadeiro para a partícula elétron-direita também é verdadeiro para a partícula pósitron-direita, e o que é verdadeiro para a partícula pósitron-direita é verdadeiro para a partícula elétron-esquerda. Mas P altera as partículas elétron-esquerda e elétron-direita, então obviamente isso não é simetria; C muda o elétron para a esquerda e o pósitron para a esquerda e, como a partícula do pósitron para a esquerda não é afetada pela interação fraca, C também não é uma simetria. No entanto, a CP altera as partículas elétron-esquerda e pósitron-direita, e ambas estão sujeitas a fraca interação nuclear.


Fig. 4

CP também não é simetria

Mas na década de 1960, constatou-se que o SR também é perturbado pela fraca interação nuclear. Novamente, isso foi uma surpresa, hoje compreensível, mas ainda sendo explorada por nós. Aqui está uma pequena história.

A maioria dos hádrons (partículas constituídas por quarks, antiquarques e glúons) decai quase instantaneamente por meio de forte interação nuclear, com intervalos de tempo inferiores a um trilionésimo de trilionésimo de segundo. Um hadron, próton, é estável; o nêutron em si vive 15 minutos. (Núcleos atômicos que consistem em prótons e nêutrons também são chamados de hádrons, mas pessoalmente prefiro chamá-los de "conjuntos de hádrons"). Mas, para vários hádrons de importância histórica e prática, a vida útil, embora pequena, não é muito boa - algo entre um bilionésimo de trilionésimo de segundo e um bilionésimo de segundo - e a maioria decai devido à fraca interação nuclear (outros decaimento através da interação eletromagnética). E em alguns deles - especialmente mésons contendo um quark inferior ou um antiquark inferior - decaimentos que violam o SR foram medidos. Outros sinais de violação da PC estão nas oscilações entre dois hádrons, semelhantes às oscilações de neutrinos.

Esse tipo de violação de CP é muito interessante porque ocorre naturalmente onde há três ou mais aromas ou gerações de quarks superiores (superior, encantado e verdadeiro) e três aromas de quarks inferiores (inferior, estranho e charmoso). Como Kobayashi e Maskawa apontaram, em uma versão do Modelo Padrão contendo apenas duas gerações, não poderia haver tal violação da RS; ele deveria ter uma razão completamente diferente. Como eles observaram isso muito antes da descoberta da terceira geração de partículas, eles, de fato, previram a existência da terceira geração, pela qual receberam o Prêmio Nobel de Física em 2008 em seguida (junto com Nambu por seu grande trabalho em outros campos).

Até o momento, não há sinais de violação do PC de natureza diferente da de Kobayashi e Maskawa. Porém, se houver partículas e interações que não sejam conhecidas pelo Modelo Padrão, pode haver outras condições em que a CP é violada.

No entanto, mesmo dentro do Modelo Padrão, há um grande mistério.

Forte interação nuclear e SR

É muito inesperado que o SR não seja significativamente perturbado por uma forte interação nuclear, e ninguém sabe por que isso acontece. Sabemos que uma interação forte não viola muito o superlátice por causa de uma determinada propriedade do nêutron, conhecida como momento do dipolo elétrico .

Um nêutron é um hadron eletricamente neutro muito semelhante a um próton. Os quarks, antiquarks e glúons que compõem o nêutron são mantidos juntos por uma forte interação nuclear. Uma pergunta interessante pode ser feita sobre qualquer momento eletricamente neutro - ele possui um dipolo elétrico.

O ímã com o qual você brincava quando criança é um dipolo magnético que possui os polos norte e sul (Fig. 5). Um monopolo magnético seria o pólo norte ou sul; mas você nunca viu isso, e ninguém viu. Um dipolo elétrico tem uma carga elétrica nula, mas por um lado possui cargas positivas e, por outro lado, cargas negativas. Pode ser um caso tão simples como um átomo de hidrogênio, com um elétron no papel de uma carga negativa e um próton no papel de uma carga positiva.

Para um dipolo elétrico simples, composto por duas cargas separadas por uma distância D, uma das quais possui uma carga q e a outra -q, o momento do dipolo elétrico é simplesmente definido como q × D. Observe que, se as cargas positiva e negativa estiverem em um só lugar, então tal objeto não tem um momento dipolar; as cargas devem ser separadas no espaço para que “polarizem”. O átomo de hidrogênio geralmente não é polarizado. Mas muitas moléculas têm um momento dipolar, embora sejam eletricamente neutras. Por exemplo, uma molécula de água H ₂ O tem um momento dipolar de 3,9 × 10 ^-8 e cm de tamanho, onde “e” é a carga de próton (e é a carga de elétrons) e cm é de 1 centímetro. Para comparação, isso é apenas um pouco menor do que o que pode ser obtido diluindo o elétron e o próton a uma distância aproximadamente igual ao tamanho da molécula de água (para esse dipolo, o momento do dipolo seria da ordem de 9 × 10 ^-8 e cm). Isso sugere que os elétrons de dois átomos de hidrogênio no H ₂ O passam muito tempo com o átomo de oxigênio.


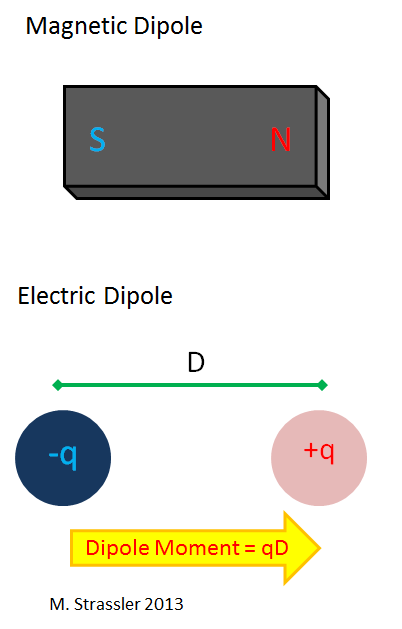Fig. 5

Qual o tamanho do momento dipolar de nêutrons? O raio de nêutrons é da ordem de 10 a ¹³ cm; portanto, seria de esperar que D fosse aproximadamente o mesmo. E consiste em quarks, antiquarks e gluons; os glúons são eletricamente neutros, mas os quarks e antiquarks têm cargas elétricas: 2/3 e (quark superior), –1/3 e (quark inferior), –2/3 e (antiquark superior) e +1/3 e (antiquark inferior) ) Então, seria de esperar que q fosse algo assim. Acontece que seria de esperar que a magnitude do momento dipolar elétrico do nêutron estivesse entre 10 e ¹³ e ^cm.É um milhão de vezes menor que o momento dipolar de uma molécula de água, principalmente porque o raio do nêutron é menor que um milhão de vezes.

De fato, alguns efeitos não óbvios nos dão uma estimativa de um tamanho ainda menor. A expectativa real é de 10 a ¹⁵ e cm.

Mas se o nêutron tiver um momento de dipolo elétrico, isso violaria T e, portanto, CP, se CPT puder ser considerado pelo menos simetria aproximada (isso também viola P). Portanto, se CP e CPT fossem simetrias exatas, o dipolo de nêutron elétrico teria que ser zero.

Certamente, já sabemos que o PC não é uma simetria exata; é quebrado por uma interação nuclear fraca. Mas a interação fraca é tão fraca (pelo menos em relação aos nêutrons) que pode dar ao nêutron um momento dipolo de elétron da ordem de 10 a ³² e cm. Isso é muito menos do que podemos medir! Portanto, para nossos propósitos, pode ser considerado zero.

Mas se a forte interação que mantém o nêutron unido viola o superlátice, esperamos que a magnitude do momento do dipolo elétrico seja de 10 a ¹⁵ e cm.No entanto, o experimento mostra que o momento do dipolo elétrico do nêutron é inferior a 3 × 10 ^-26 e cm! Isso é dez mil milhões de vezes menos que o esperado. Portanto, uma forte interação nuclear não viola o superlattic com a força esperada.

Por que é tão menor que o esperado? Ninguém sabe, embora tenha havido muitas suposições. Esse enigma é chamado de forte problema de PC e é um dos três maiores problemas que afetam a física de partículas, junto com o problema de hierarquia e o problema constante cosmológico .

Especificamente, o problema é o seguinte. Se você escrever a teoria da interação nuclear forte - as equações para glúons, quarks e antiquarks, chamadas QCD -, essas equações terão parâmetros diferentes, a saber:

• A força unificadora de forte interação nuclear,
• massas de diferentes quarks,
• ângulo teta, que não afeta os diagramas de Feynman, mas determina os efeitos de vários processos sutis (tunelamento quântico, instantons , pseudopartículas) da física dos glúons.

Parar o que? Qual é esse último item? Bem, esse parâmetro QCD opcional foi descoberto na década de 1970 (essa é uma das áreas em que Alexander Polyakov , que recentemente ganhou o prêmio, ficou famoso). O problema em si é de natureza técnica demais para ser descrito aqui, mas basta dizer que, se o ângulo teta não for 0 ou π, uma forte interação nuclear viola o superlattice. Mais precisamente, a CP viola uma certa combinação de ângulo teta e massas de vários quarks (especificamente, o produto das fases complexas de suas massas). E esses dois parâmetros (ângulo teta e massas de quarks) não têm uma conexão óbvia - então como eles se combinam para serem perfeitamente compensados? No entanto, por algum motivo, sua combinação é zero, ou pelo menos dez bilhões de vezes menor do que poderia ser. Não há razões óbvias para isso.

As explicações a seguir podem ser dadas para esse enigma, com quase 40 anos de idade:

• o quark superior pode não ter massa (isso é muito difícil de verificar, pois não pode ser medido diretamente; métodos indiretos há muito tempo dizem que sua massa é várias vezes a massa de um elétron, mas algumas sutilezas não nos permitem interpretar esses métodos com total segurança).
• Talvez exista um campo de axion que remova esse efeito; essa idéia prevê a existência de uma partícula axial, que é procurada há mais de 30 anos, mas ainda não foi encontrada.Axion, a propósito, também poderia desempenhar o papel da matéria escura do Universo.

Existem algumas outras soluções possíveis para esse problema, mas não as descreverei aqui; infelizmente, em geral, eles não têm conseqüências experimentais óbvias que possam ser verificadas em um futuro próximo.