O universo começou não com o Big Bang, mas com o Big Thaw

Constante cosmológica e criação do Universo

No que diz respeito ao universo, existem dois enigmas não resolvidos particularmente dolorosos, um dos quais está relacionado ao seu destino final e o segundo - ao começo, cosmólogos intrigantes por décadas. A comunidade científica sempre acreditou que essas duas tarefas são independentes uma da outra - mas e se não for?

A primeira tarefa está relacionada à existência de algo chamado "energia escura", que hoje acelera a expansão do Universo e, finalmente, determina seu destino final. Os teóricos dizem que a ação da energia escura pode ser explicada através da introdução de um novo termo nas equações de Einstein chamado "constante cosmológica". Mas, para que essa explicação funcione, a constante cosmológica deve ter um valor muito pequeno. Em unidades naturais, é determinado por uma unidade dividida por um número composto por 123 dígitos! Uma explicação do valor dessa constante é um dos problemas mais difíceis da física teórica.


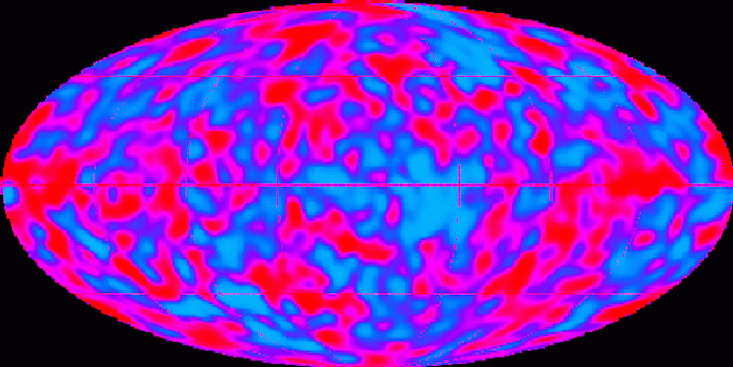Variações CMB indicam flutuações de densidade no início do Universo

O segundo problema está associado a outro número importante que define o nosso universo e à formação de estruturas como galáxias e grupos de galáxias. Sabemos que o Universo primitivo, embora fosse muito homogêneo, continha pequenas flutuações na densidade, que se tornaram as causas das estruturas cósmicas que vemos hoje. Para coincidir com nossas observações, essas flutuações tinham que ter um certo tamanho e forma. Como essas flutuações apareceram nos primeiros períodos da evolução do Universo, e sua forma e tamanho, é um mistério igualmente surpreendente da cosmologia.

Dada a abordagem geralmente aceita da cosmologia, esses dois números - a magnitude da constante cosmológica e a magnitude das perturbações iniciais - não são considerados relacionados. Afinal, um deles lida com a fase mais antiga do universo, e a segunda com a mais recente, e eles são separados pelo tempo cósmico de 14 bilhões de anos. Além disso, a cosmologia padrão não explica esses valores com base em princípios fundamentais. Os modelos geralmente aceitos do Universo não dizem nada sobre o valor numérico da constante cosmológica ou predizem valores completamente diferentes. Em relação à magnitude das perturbações iniciais, a abordagem mais popular é obter esse valor da classe de modelos que descrevem a inflação - um período de rápido crescimento na fase inicial da existência do Universo. O problema dos modelos inflacionários é que eles podem ser ajustados para produzir quase qualquer resultado, razão pela qual eles não têm uma capacidade preditiva.

Em meu trabalho recente, realizado com minha filha Hamsa Padmanabhan e Tomalla Fellow, na Escola Técnica Superior Suíça de Zurique, esses dois números estão associados à cosmogênese - a criação do Universo - e seu significado exato é explicado. Nosso trabalho, publicado recentemente nas Letras de Física B, mostra que a própria existência de uma constante cosmológica, bem como seu pequeno valor, pode ser representada como uma conseqüência direta do conteúdo informacional do espaço-tempo [Padmanabhan, T. & Padmanabhan, H. Informação cósmica, a informação cosmológica. constante e a amplitude de perturbações primordiais. Letras de Física B 773, 81-85 (2017)]. Além disso, a análise fornece o valor correto para o tamanho e a forma de pequenas flutuações do Universo primitivo.

A notável interconexão dessas constantes fundamentais é essencial para nossa compreensão do universo. Em particular, isso muda nossa compreensão do Big Bang e elimina a necessidade de um período de inflação nos estágios iniciais do universo.

O Big Bang é provavelmente a característica mais famosa da cosmologia padrão. Mas ele também não é realmente necessário para ela. O modelo clássico do Universo, descrito pelas equações de Einstein, deixa de funcionar nas condições do Big Bang, com densidade e temperatura infinitas - é a situação que os físicos chamam de singularidade.

Mas e se não houvesse singularidade? Desde a década de 1960, os físicos vêm trabalhando para descrever o Universo sem o Big Bang, tentando combinar teoria da gravidade e teoria quântica em algo chamado "gravidade quântica". Os físicos John Wheeler e Bryce DeWitt foram os primeiros a aplicar essas idéias à hipotética fase dogométrica do Universo, na qual os conceitos de espaço e tempo ainda não emergiram de uma estrutura desconhecida. Isso levou ao surgimento da cosmologia quântica, na qual os físicos tentam descrever a dinâmica de modelos simples de brinquedos do universo na linguagem quântica. Desnecessário dizer que, ao longo das décadas, várias idéias diferentes, embora relacionadas, para descrever a fase pré-geométrica surgiram subitamente. O que os une é que o Universo clássico, sem singularidade, aparece através de uma série de transformações da fase pré-geométrica para aquela em que o espaço-tempo é descrito pelas equações de Einstein. A principal dificuldade na construção dessa descrição é que não temos uma teoria completa da gravidade quântica que nos permita modelar a fase pré-geométrica em detalhes.


Einstein chamou seu vício à constante cosmológica várias vezes de um erro grosseiro em suas equações. Hoje, os físicos acreditam que isso tem um significado positivo.

O principal ingrediente que introduzimos para ajudar a contornar essa complexidade técnica é o conceito de informação espacial. Recentemente, a ideia de que a informação deve desempenhar um papel fundamental na descrição da física está ganhando cada vez mais apoio. Aparece em vários casos quando os cientistas estão tentando combinar os princípios da teoria quântica e da gravidade - por exemplo, no estudo de buracos negros quânticos. Além disso, em alguns desses modelos, existe uma idéia intrigante de holografia, que afirma que o conteúdo informativo de uma grande região pode estar relacionado ao conteúdo informativo de suas fronteiras. Infelizmente, porém, a descrição matemática da informação em diferentes casos é diferente e o princípio unificador, aplicável em todos os casos, ainda não foi encontrado. Portanto, para aplicar a idéia de informação a todo o universo, primeiro precisamos criar uma definição fisicamente apropriada para ele.

A definição das informações espaciais que usamos pode ser descrita por analogia. Quando um pedaço de gelo derrete e se transforma em água, ocorre uma transição de fase do sólido para o líquido. Os processos reais de transição de fase podem ser extremamente complexos, mas o número total de átomos de gelo será o mesmo que o número de átomos de água. Este número determina o número de graus de liberdade do sistema que não muda durante a transição de fase. Da mesma forma, a transição de fase que levou ao surgimento do Universo pode ser descrita por um número que relaciona o número de graus de liberdade na fase pré-geométrica à quantidade inerente ao espaço-tempo clássico. Usando esse número, que chamamos de CosmIn, podemos combinar as duas fases do universo e contornar as complexidades do modelo completo de gravidade quântica.

Cosmin, como um número fisicamente observável, deve ser finito. Na ausência de singularidades, acreditamos que todas as quantidades físicas devem ser finitas. Além disso, fomos capazes de mostrar que o cosmin será finito apenas se o Universo experimentar uma fase acelerada de expansão no período tardio da existência - como observamos hoje. Essa conexão não apenas indica a existência de uma razão fundamental para a existência de uma constante cosmológica, mas também sobre os métodos de cálculo de seu valor numérico - se soubermos o valor do cosseno.

O valor da cosmina na fase pré-geométrica ou gravitacional quântica do Universo pode ser determinado usando os resultados que aparecem periodicamente em diferentes modelos de gravidade quântica. Acontece que a quantidade total de informações transferidas da fase gravitacional quântica para a fase clássica deve ser igual a um número simples: 4π, a área de uma esfera de raio unitário. Usando esse fato, podemos relacionar o valor numérico da constante cosmológica com a escala de energia, na qual o Universo passou da fase gravitacional quântica para a clássica.

Essa escala de energia da transição pode ser associada à segunda propriedade misteriosa do nosso Universo: a magnitude das pequenas flutuações quânticas no Universo primitivo que cresceram e formaram as galáxias e aglomerados galácticos que vemos hoje. Um sistema popular para calcular o tamanho dessas flutuações usa modelos inflacionários do Universo que descrevem o Universo passando por uma incrível expansão rápida e grande em tamanho. Mas existem muitos modelos inflacionários e eles são muito diferentes e podem fornecer qualquer valor desejado. Também é importante notar que o formato das flutuações iniciais foi obtido por Edward Robert Harrison em 1970 (e independentemente por Jacob Zeldovich), e é chamado de espectro de Harrison-Zeldovich. Mas as pessoas esquecem de salientar que Harrison obteve seu resultado mais de dez anos antes da invenção dos modelos inflacionários!

Nosso modelo nos permite relacionar as duas grandezas - o valor da constante cosmológica e o tamanho das flutuações iniciais - com a escala de energia na qual o universo pré-geométrico experimentou uma transição de fase e se tornou o universo clássico em que vivemos. E atenção, quando selecionamos a escala de energia correta, obtemos o valor correto observado para ambos os valores. Isso nos leva a uma relação algébrica entre a constante cosmológica, a magnitude das flutuações iniciais e a cósmica. Podemos inverter essa relação usando os parâmetros cosmológicos observados e verificar se o valor de cosmin é realmente 4π. A teoria passa no teste perfeitamente; descobrimos que o cosmin determinado a partir das observações é 4π com uma precisão de 1/1000.

Surpreendentemente, uma combinação complexa de parâmetros cosmológicos, considerados não relacionados entre si, tem um significado tão simples. Uma abordagem comum seria considerar esse relacionamento como coincidência aleatória. Acreditamos que ela está nos dizendo algo profundo e bonito sobre o nosso universo.

Acreditamos que fizemos a primeira tentativa de relacionar o valor numérico da constante cosmológica ao tamanho das flutuações no Universo primitivo e obter esses dois valores a partir de um modelo que não possui parâmetros ajustáveis ​​e os associa à escala de energia na qual o Universo começou a existir.

Todas essas idéias existem em uma plataforma mais geral de gravidade quântica, uma teoria que os físicos, apesar de quase cinco décadas de desenvolvimento, ainda não possuem. Uma das vantagens do nosso modelo é que ele não requer os detalhes da gravidade quântica. Mas ela faz duas pistas importantes sobre a natureza da gravidade quântica e a estrutura do espaço-tempo. Em primeiro lugar, ela diz que o espaço-tempo deve ser representado como consistindo em graus microscópicos de liberdade, assim como na matéria que consiste em átomos. Em segundo lugar, ela argumenta que a teoria correta da origem do universo deve incluir uma transição de fase da fase pré-geométrica para a fase clássica.

Essas dicas podem responder a uma pergunta-chave: por que, após várias décadas de trabalho, os teóricos não combinaram a teoria quântica e gravidade? Acreditamos que isso é melhor explicado por outra analogia. Sabemos que a dinâmica dos fluidos é uma teoria física consistente, expressa através de um conjunto de equações. Se os tomarmos como fundamentais e aplicarmos os princípios da teoria quântica a eles, podemos descobrir um novo fenômeno interessante - por exemplo, fônons (quanta de vibração) e suas interações. No entanto, usando essa abordagem, não seremos capazes de chegar à estrutura quântica da matéria.

Há evidências de que as equações que descrevem a gravidade nesse sentido são semelhantes à dinâmica de fluidos. Em outras palavras, reformular as equações que descrevem a gravidade usando os princípios da teoria quântica é semelhante à aplicação dos princípios quânticos às equações da dinâmica de fluidos. Não descobriremos a estrutura quântica do espaço-tempo dessa maneira - e acreditamos que, por essa década, as tentativas de quantificar a teoria de Einstein terminaram em um alto fracasso.

Em vez disso, precisamos repensar a natureza da gravidade e entender o que ela nos diz sobre a estrutura microscópica do espaço-tempo. O físico Ludwig Boltzmann usou essa abordagem para entender que os fenômenos de temperatura exigem que a noção de matéria consista em graus discretos de liberdade (em outras palavras, átomos). Boltzmann, de fato, disse que se algo pode estar quente, deve conter graus microscópicos de liberdade.

O espaço-tempo também pode ter uma temperatura e parecer quente para certos observadores. Essa ideia surgiu graças ao trabalho de Jacob Beckenstein e Stephen Hawking no contexto de buracos negros. Logo depois, em meados dos anos 70, o trabalho de Bill Unrich e Paul Davis mostrou que essa é a principal propriedade do espaço-tempo. Ao combinar o paradigma de Boltzmann com o fato de que o espaço-tempo - como a matéria comum - pode ser quente, você chega à conclusão de que o espaço-tempo deve ter graus de liberdade internos, como átomos na matéria. Evidências teóricas em apoio a essa conclusão começaram a surgir nos últimos anos [Padmanabhan, T. Os átomos do espaço-tempo e a constante cosmológica. Journal of Physics: Conference Series 880, 012008 (2017)]. Essa observação contém a chave para entender a microestrutura do espaço-tempo, o que rapidamente leva a resultados notáveis.

Em primeiro lugar, a evolução de um site espaço-temporal pode ser descrita em termos de graus de liberdade (ou, equivalentemente, de conteúdo informativo) localizados dentro dos limites deste site. Em segundo lugar, a gravidade se torna insensível a mudanças no nível de energia zero. Na teoria de Einstein, a gravidade é responsável pela quantidade absoluta de energia, razão pela qual é quase impossível calcular a constante cosmológica. Mas para um paradigma baseado no conteúdo da informação, não é assim. Terceiro, a abordagem informacional sugere que não devemos imaginar a evolução cósmica de acordo com uma certa solução das equações de Einstein. Essas equações surgem de um conjunto mais preciso de equações que descrevem os graus quânticos de liberdade do espaço-tempo [Padmanabhan, T. Nós realmente entendemos o cosmos? Comptes Rendus Physique 18, 275-291 (2017)].

A abordagem da informação, confirmada pelo nosso modelo de cosmina, nos dá uma imagem nova e vívida do Universo, semelhante a um grande pedaço de gelo contendo uma fonte de calor. Uma fonte de calor derrete o gelo ao seu redor, criando uma seção de água que se expande, alcançando o equilíbrio termodinâmico local. Em larga escala, mais próximo do limite da fase, as moléculas ainda não alcançaram o equilíbrio, pois um pedaço de gelo é aquecido por dentro. Curiosamente, isso é muito semelhante ao comportamento do nosso universo. Uma parcela de água é semelhante ao Universo observável (descrito pela teoria de Einstein). Está cercado por uma fase pré-geométrica (semelhante ao gelo), descrita por até agora leis desconhecidas da gravidade quântica. A idéia do Big Bang desaparece e, em vez disso, aparece uma transição de uma fase para outra ao longo da fronteira. A necessidade de um período inflacionário também desaparece.

Toda a plataforma é simples e elegante, pois é descrita por um único parâmetro: a escala de energia da transição de fase do Universo primitivo da pré-geometria para a geometria de Einstein. Isso difere dos modelos inflacionários convencionais que contêm muitos parâmetros e não possuem capacidade preditiva. Nosso modelo não usa física não verificada. O único postulado que fizemos é que o conteúdo do Universo deve ser igual a 4π, ​​a área da superfície de uma única esfera.

O trabalho abre três novas áreas de pesquisa. Primeiro, ela nos convida a estudar a física da fase pré-geométrica em vários modelos de gravidade quântica. Segundo, fornece uma oportunidade para estudar a idéia de informações espaciais usadas neste trabalho e tentar conectá-las a outras idéias semelhantes usadas em outros contextos. Terceiro, reforça a ideia de que o espaço-tempo consiste em graus mais elementares de liberdade - assim como a matéria consiste em átomos - e nos encoraja a estudar as várias fases do espaço-tempo da mesma maneira que estudamos as várias fases da matéria na física da matéria condensada .

Tanu Padmanabhan é professora do Centro Interuniversitário de Astronomia e Astrofísica da Índia.