Como imaginar dimensões extras: mundos unidimensionais

Quando falo com uma pessoa distante da física sobre possíveis dimensões adicionais do espaço desconhecidas para nós, uma das perguntas mais frequentes é: “Como você imagina dimensões adicionais? Só consigo imaginar três e não entendo como ir além; não faz sentido para mim.

O que nós físicos não fazemos (pelo menos nenhum de meus conhecidos afirmou estar fazendo isso), por isso não imaginamos dimensões adicionais. Meu cérebro é limitado como o seu e, embora ele crie facilmente uma imagem tridimensional do mundo para a qual eu possa me mover, não posso forçá-lo a representar uma imagem de um mundo quadridimensional ou quadridimensional, como você. Minha sobrevivência não dependia da capacidade de imaginar algo assim, então talvez não seja surpreendente que meu cérebro não esteja sintonizado com isso.

Em vez disso, eu (e a julgar pela nossa troca de idéias, a maioria dos meus colegas também) desenvolvo a intuição com base em uma combinação de analogias, truques de visualização e cálculos. Nós omitimos os cálculos aqui, mas muitas analogias e truques não são tão difíceis de explicar.

Reflexões sobre dimensões adicionais podem ser aprendidas em duas etapas.

1. Um passo simples é aprender a imaginar ou descrever o mundo com dimensões adicionais. Você já conhece várias maneiras de fazer isso, mesmo que não esteja ciente disso - e pode aprender um pouco mais.
2. O estágio mais difícil é aprender como tudo funciona no mundo com dimensões adicionais. Como trabalhar com uma agulha em quatro dimensões, e não em três; se os planetas se moverão em órbitas ao redor do sol em seis dimensões espaciais; prótons e átomos se formarão? Aqui você precisará aprender truques desconhecidos, representando as diferenças entre um mundo com apenas uma ou duas dimensões e um mundo tridimensional conhecido por nós, e trabalhando por analogia.

Então, vamos começar ajudando você a imaginar o mundo com dimensões extras. Para fazer isso, você precisa pensar em como, em geral, representamos qualquer dimensão. Vamos começar do começo.

• Um mundo com zero dimensões é um ponto. Pouco se pode dizer sobre ele agora, mas retornaremos a ele.
• O mundo unidimensional já é bastante interessante.
• Nos mundos bidimensionais, coisas muito mais interessantes estão acontecendo.
• É importante evitar confusão entre as dimensões espaciais e o significado mais geral da palavra "dimensão" na linguagem comum, bem como em matemática e estatística.
• E então vários exemplos de dimensões adicionais se seguirão, com ênfase no que exatamente significa “adicional”, e como pode ser que em nosso mundo haja dimensões sobre as quais nada sabemos.
• Também examinaremos como exatamente essas medições invisíveis podem ser detectadas.

Mundos unidimensionais

Um mundo com uma dimensão espacial é muito mais simples que um mundo com três, mas há algo nele que pode ser fundamentado. Por exemplo, existem vários tipos de mundos unidimensionais. Eles têm não apenas certas propriedades comuns, mas também diferenças interessantes.

Para o primeiro exemplo, vamos considerar a medição não como um conceito físico, mas como um conceito mais geral. Isso o ajudará de várias maneiras, por exemplo, distraindo sua intuição de equívocos naturais sobre o que são dimensões e como elas funcionam. Vamos falar sobre ganhos anuais - quanto dinheiro uma pessoa recebe por um determinado ano. Essa é uma dimensão de estudo tão adequada quanto todos os outros.

Mensuração de receita

Sua renda no ano passado é um determinado número em sua moeda local. Pode ser positivo ou negativo, grande ou pequeno; pode ser representado como um ponto em uma linha, como na fig. 1, que chamaremos de "ponto de renda". Cada ponto na linha representa um possível retorno.


Fig. 1: uma linha de receita de comprimento infinito, cujo lado esquerdo representa perdas e o lado direito representa renda.

O que torna a renda anual uma propriedade unidimensional é (muito aproximadamente) o seguinte:

• A posição no espaço é indicada por uma unidade de informação: no nosso caso, por renda.

Observe também que é contínuo (ou quase contínuo) - se duas pessoas têm renda diferente A e B, podemos encontrar um terço cuja renda está entre A e B.

Esses dois fatos implicam que a renda pode mudar continuamente ao longo da linha de renda, movendo-se para a direita ou esquerda - para uma renda mais alta ou mais baixa. Não há outras opções.

Obviamente, a linha de receita não tem nada a ver com o espaço físico no qual você e eu podemos caminhar, mas isso ainda é uma dimensão. E (pelo menos em princípio) ele não tem fim em nenhuma das partes: não há (em princípio) nenhum limite de quanto dinheiro uma pessoa pode ganhar ou perder em um ano. Este mundo unidimensional não é tão diverso, mas ainda podemos fazer algumas perguntas significativas sobre ele:

• Como as receitas anuais são distribuídas nos EUA?
• Qual é a renda média anual no Japão?
• Como as respostas a essas perguntas mudam com o tempo?

Essas perguntas fazem sentido no mundo unidimensional da linha de receita.

Medição do arco-íris

E aqui está outro mundo completamente diferente. Uma única dimensão é formada pelas cores do arco-íris, do vermelho, ao laranja, ao amarelo, de lá ao verde, [azul], azul e violeta. [As pessoas que falam inglês têm seis cores em um arco-íris, não emitem azul / aprox. transl.]. Desse ponto de vista, as cores formam um mundo unidimensional de tamanho finito. Fora do vermelho ou roxo, existem formas invisíveis de flores, mas, do ponto de vista dos seus olhos, a medição termina nelas. Agora, é apresentado não na forma de uma linha infinita, mas na forma de um segmento - a “linha do arco-íris” na Fig. 2. Por favor, não confunda com a roda de cores - se estiver fechada, nossa medição começa em vermelho e termina em roxo. E, novamente, a posição na linha do arco-íris é determinada por uma unidade de informação (cor) e é contínua.


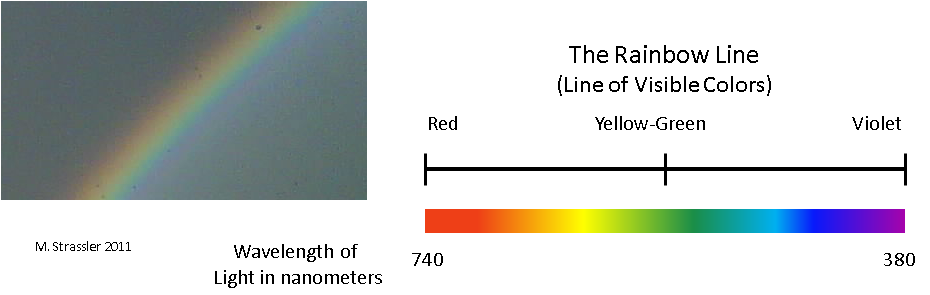Fig. 2

Obviamente, isso também não é uma medida do espaço físico! Você pode jogar uma bola da sua casa para a casa do vizinho, mas não consegue imaginar como joga uma bola de verde para laranja - não faz sentido. E ainda será também uma dimensão. Aqui você pode fazer muitas perguntas significativas: como a cor da maçã se move ao longo da linha do arco-íris no processo de transformar uma maçã de verde em vermelha? Quantos na luz do sol de cada uma das flores? Se uma estrela laranja começar a ficar vermelha, ela ficará amarela primeiro?

Medição da direção do vento

E aqui está a terceira opção de medição, e novamente outra. Se você ouvir a previsão do tempo, será informado que o vento começará a soprar em breve do norte, do noroeste ou do sudoeste. As direções possíveis do vento também são uma medida. Por favor note que esta não é uma dimensão espacial! Nesta dimensão, você não pode jogar a bola da maneira que você a joga para cima, para a esquerda ou para a frente. Esta é uma medida das direções no espaço!


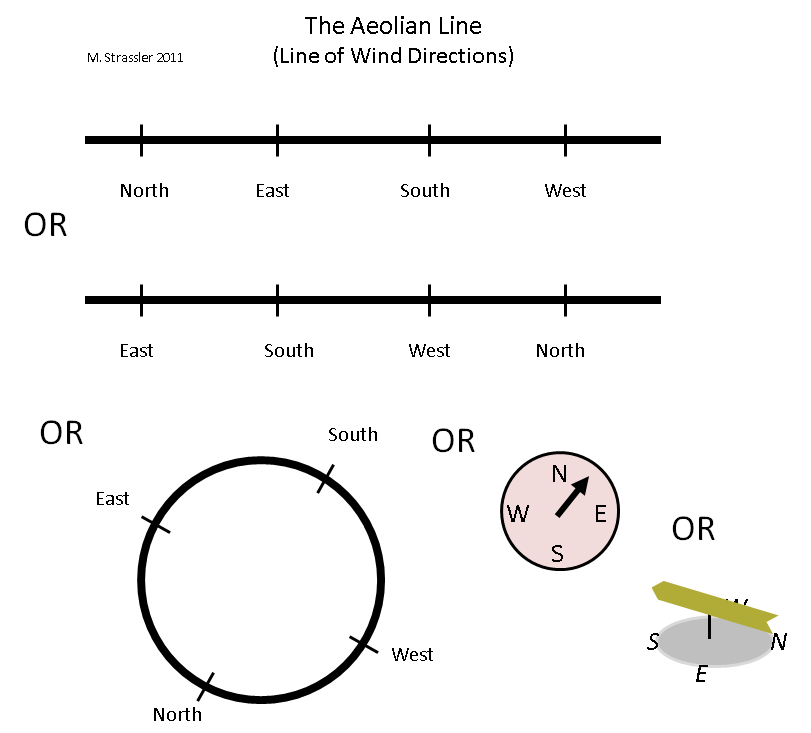Fig. 3

Como essa dimensão pode ser representada? Existem pelo menos dois métodos naturais para isso, mostrados na fig. 3. Utilizamos o segmento - a "linha Eólia" ( Éolo é um semideus, o governante dos elementos aéreos dos gregos antigos) - mas a linha Eólia difere da linha do arco-íris em sua frequência. A direção do vento pode mudar de norte para leste, depois para o sul, depois para o oeste e depois novamente para o norte, continuamente. E, a nosso ver, a linha pode ser cortada em qualquer lugar - compare as duas linhas na parte superior da Fig. 3, que representam igualmente bem a linha eólica. A linha inferior é que o vento pode ir da extremidade direita da linha diretamente para a extremidade esquerda e vice-versa, por isso não importa onde cortá-lo. Ou talvez a maneira mais fácil de representar essa linha periódica seja na forma de um círculo. É isso que estamos fazendo com uma bússola ou cata-vento!

Três mundos unidimensionais diferentes

E aqui você tem mundos unidimensionais. Veja como eles são ricos em detalhes! Tamanhos diferentes, propriedades diferentes. Na linha de renda, a renda pode aumentar ou diminuir para sempre. Na linha do arco-íris, seus olhos só podem se mover para roxo, ou o contrário, apenas para vermelho. E na linha Eólia, o vento pode fazer um círculo completo o quanto você quiser - mas, ao mesmo tempo, sempre retornará a uma das direções.

Essas variedades de mundos unidimensionais - infinito, finito e finito-periódico, representados por uma infinita linha, segmento e círculo - são os ingredientes básicos para entender os mundos de dimensões superiores. Vou contatá-los mais de uma vez. Na fig. 4 são apresentados, assim como o quarto tipo, estendendo-se infinitamente em apenas uma direção. Um exemplo dessa medição pode ser a temperatura: ela pode ser arbitrariamente grande, mas a temperatura mais baixa possível - zero absoluto -, então a temperatura forma uma linha que começa no zero absoluto e sobe a partir daí, mas não para baixo.


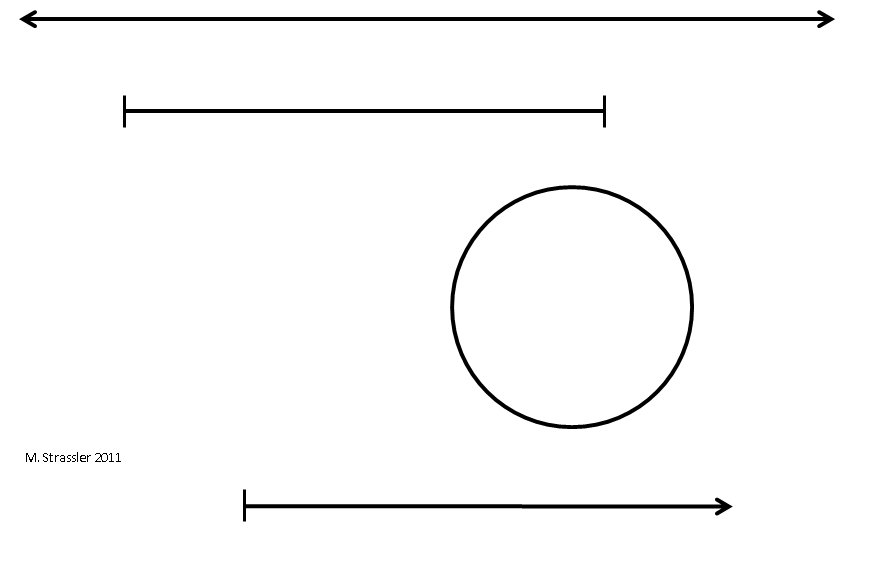Fig. 4

Como representar dimensões, espacial e outras

Mencionei casualmente ou usei vários métodos diferentes para representar medições. A renda pode ser representada por um número ou uma linha sem fim. O arco-íris visível pode ser representado como um segmento ou como uma cor e também usar um número - o comprimento de onda dos fótons correspondente a uma determinada cor. A direção do vento pode ser representada por um círculo ou um segmento cuja extremidade esquerda está conectada à direita - ou palavras como norte, leste, sul, oeste - ou um número que define a direção em graus, indo de 0 a 360 e retornando a 0. O que podemos apresentar uma dimensão de várias maneiras diferentes nos dá uma enorme flexibilidade para treinar o trabalho intuitivo com dimensões extras.

Para ilustrar esses tipos de medidas, escolhi conceitos que não têm nada a ver com espaço físico - renda, cor do arco-íris, direção do vento - para mostrar que as medições espaciais são exemplos concretos de um conceito de medição mais geral. Compreender esse fato facilita muito as tentativas de imaginar mundos com mais de três dimensões. Lembre-se, mencionei duas partes do processo de pensamento sobre dimensões extras? Primeiro, aprenda a representá-los; segundo, entenda como tudo funciona e funciona neles. As dimensões espaciais têm características associadas à forma como algumas coisas funcionam nelas, mas não à sua apresentação.

Mundos espaciais com uma dimensão efetiva

Diante de tudo isso, consideremos os mundos espaciais que encontramos regularmente com uma dimensão efetiva. Ou, mais precisamente, situações em que um determinado aspecto do nosso mundo se comporta como se o espaço tivesse apenas uma dimensão. Então dizemos que o mundo de certos participantes ou objetos se torna efetivamente unidimensional.


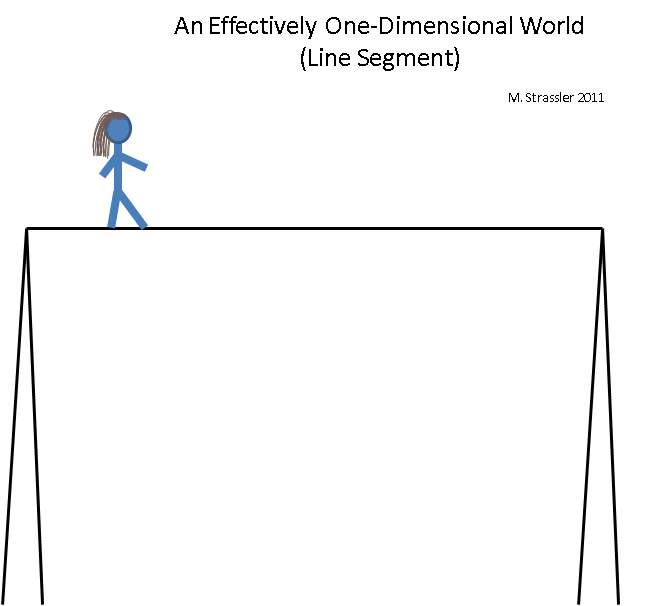Fig. 5

Imagine um equilibrista equilibrado em uma corda alta. O mundo do equilibrista é efetivamente unidimensional (embora, é claro, permaneça tridimensional), uma vez que não é capaz de se mover com segurança em nenhuma direção além da direita para a esquerda ou da esquerda para a direita. Este mundo é como um mundo de arco-íris - é finito em comprimento e, quando o equilibrista chega ao fim, ele precisa se virar e voltar (ou sair da corda, encerrando uma situação em que o mundo se torna efetivamente unidimensional). O que mais posso dizer? A posição na corda pode ser determinada por uma unidade de informação (por exemplo, a distância do poste esquerdo ao andador na corda bamba). Dois caminhantes na corda bamba podem se encontrar na mesma linha, mas não passam um pelo outro.

Podemos transformar o mundo de uma corda em uma linha eólica fechando-a em um círculo (Fig. 6). Nele, dois caminhantes na corda bamba também não podiam passar um pelo outro - esta é a principal propriedade dos mundos unidimensionais. E essa ainda seria a dimensão final. Mas o equilibrista em tal situação já podia andar em círculo continuamente e sem parar, sem parar.


Fig. 6

Outros mundos unidimensionais conhecidos (efetivamente):

• A estrada estreita é um mundo unidimensional para carros;
• Um caminho estreito com um penhasco - para um turista escalando uma montanha;
• Os pisos de um prédio são para um elevador.

Em geral, o mundo permanece tridimensional, mas para descrever um carro, um turista ou um elevador, apenas uma dimensão precisa ser representada.

No futuro, lembre-se: vivemos em um mundo tridimensional aparente, e tudo o que encontramos nos parece tridimensional. Mas às vezes nosso mundo tridimensional (mais precisamente, parte dele) pode se comportar de maneira efetivamente unidimensional ou bidimensional (você pode criar exemplos?) Ou até mesmo de dimensão zero! (Todo mundo que tem azar de ficar preso em um engarrafamento que não se mexe em lugar algum sabe o que é este mundo com zero dimensões!) Essa intuição será muito útil para nós mais tarde.