Um matemático destacado revelou os detalhes de como seus sucessos no estudo de problemas matemáticos de milênios estão relacionados a conceitos retirados da física.
Mignon KimA matemática está cheia de sistemas numéricos estranhos dos quais a maioria das pessoas nunca ouviu falar. Alguns deles serão até difíceis de imaginar. Mas
números racionais são familiares a todos. Estes são números para contar objetos e frações - todos os números conhecidos por nós no ensino fundamental. Mas, em matemática, às vezes é mais difícil entender as coisas mais simples. Eles são simples, como uma parede lisa, sem rachaduras e saliências, ou outras propriedades óbvias nas quais você pode agarrar.
Minion Kim , matemático da Universidade de Oxford, está particularmente interessado na questão de quais números racionais são adequados para resolver equações de um certo tipo. Esse problema estimulou especialistas em teoria dos números por milênios. E eles mal fizeram progressos em direção a sua solução. Quando uma pergunta é estudada há tanto tempo e sem resposta, pode-se concluir que a única maneira de avançar é apresentar uma idéia radicalmente nova. Foi exatamente o que Kim fez.
“Não existe muita tecnologia, embora tenhamos trabalhado nisso nos últimos 3000 anos. Portanto, quando alguém apresenta uma maneira verdadeiramente nova de fazer isso, é de grande interesse - e Mignon fez exatamente isso ”, disse Jordan Ellenberg, matemático da Universidade de Wisconsin em Madison.
Na última década, Kim descreveu uma maneira completamente nova de encontrar padrões no mundo aparentemente desordenado dos números racionais. Ele descreveu esse método em artigos e em conferências e o transmitiu aos estudantes que agora continuam este trabalho por conta própria. Mas ele sempre salvava alguma coisa. Sua visão, que deu vida a suas idéias, baseou-se não em um mundo puro de números, mas em conceitos emprestados da física. Para Kim, as decisões racionais são um pouco reminiscentes da trajetória da luz.
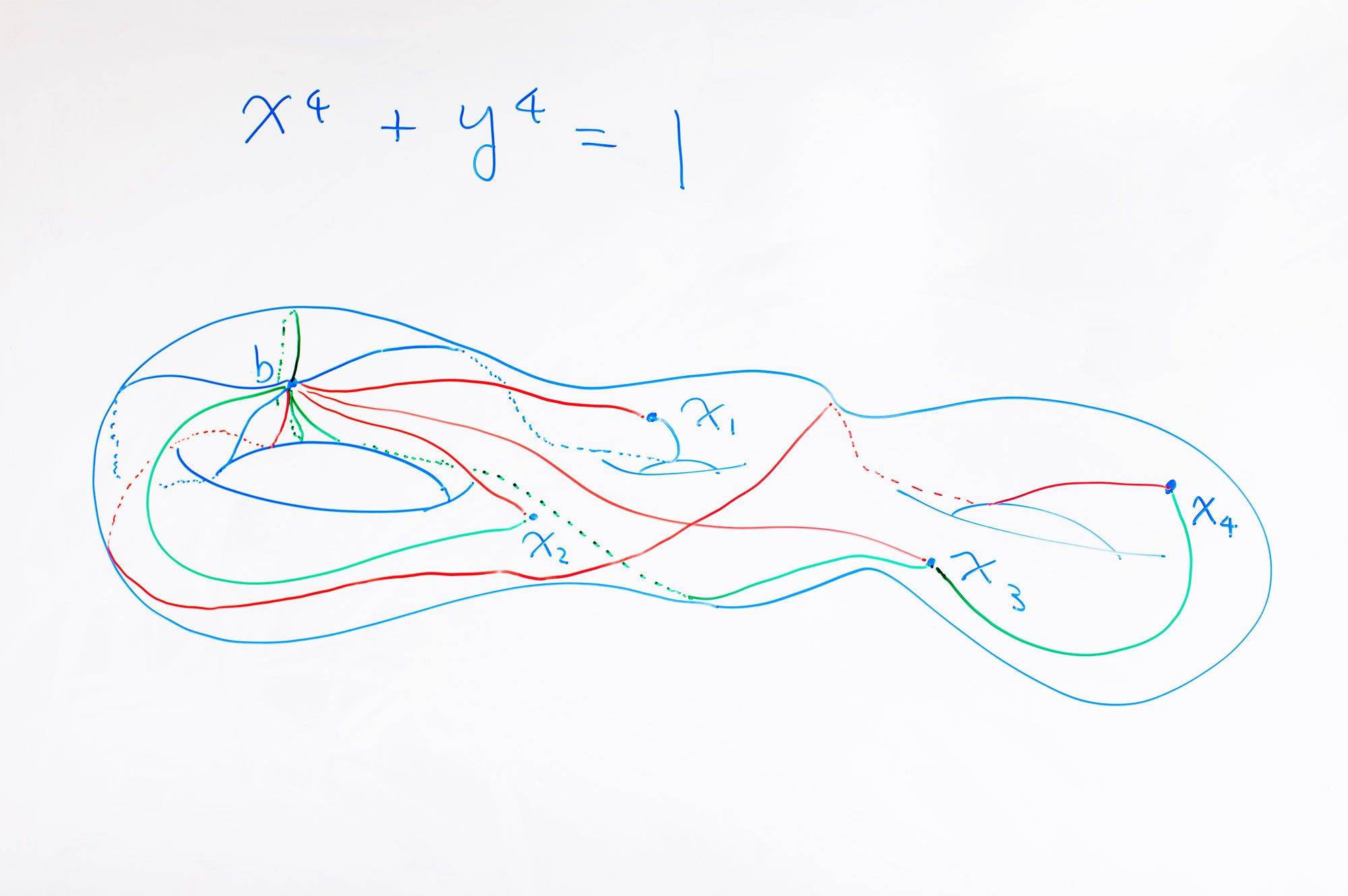Um objeto matemático, um toro de três buracos, adorna o quadro de Kim na Universidade de Oxford.Se essa conexão parece fantástica, então é, mesmo para os matemáticos. Portanto, Kim não revelou seus detalhes por um longo tempo. "Eu escondi porque durante muitos anos fiquei confuso com a conexão com a física", diz ele. "Os especialistas em teoria dos números são pessoas muito práticas, e a influência da física às vezes os torna céticos em relação à matemática."
Mas agora Kim diz que está pronto para compartilhar sua visão. "Acho que a mudança é apenas um sintoma do envelhecimento!" - escreveu Kim, que completou 53 anos, em uma das primeiras cartas que trocamos para escrever essa história.
Recentemente, ele realizou uma conferência que reuniu especialistas em teoria dos números e teoria das cordas. Ele também esboçou rascunhos de artigos começando a descrever sua inspiração para a comunidade matemática, não acostumada a pensar em números usando analogias diretas com o mundo físico.
Resta apenas um obstáculo - a última parte da analogia da física em matemática, que Kim ainda precisa resolver. Ele espera que, convidando outras pessoas a compartilhar sua visão, especialmente os físicos, receba a ajuda necessária para concluir o trabalho.
Enigma antigo
Soluções racionais de equações atraem ativamente a mente humana. Eles trazem satisfação, semelhante ao que você obtém das peças do quebra-cabeça que se encaixam no lugar. Portanto, eles são os heróis das mais famosas hipóteses matemáticas.
Os números racionais incluem números inteiros e qualquer número que possa ser expresso como a razão de dois números inteiros, por exemplo, 1, -4 ou 99/100. Os matemáticos estão especialmente interessados em números racionais que resolvem equações diofantinas - equações polinomiais com coeficientes inteiros, por exemplo, x
2 + y
2 = 1. Eles têm o nome do matemático
Diofhantus , que os estudou em Alexandria no século III d.C.
As soluções racionais são difíceis de encontrar no caso geral, pois não obedecem a nenhuma regularidade geométrica. Tome a equação x
2 + y
2 = 1. Suas soluções em
números reais formam um círculo. Remova todos os pontos do círculo que não puderem ser expressos como frações, e apenas permanecerão decisões racionais que não formam um objeto tão elegante. As soluções racionais parecem espalhadas aleatoriamente pela circunferência.
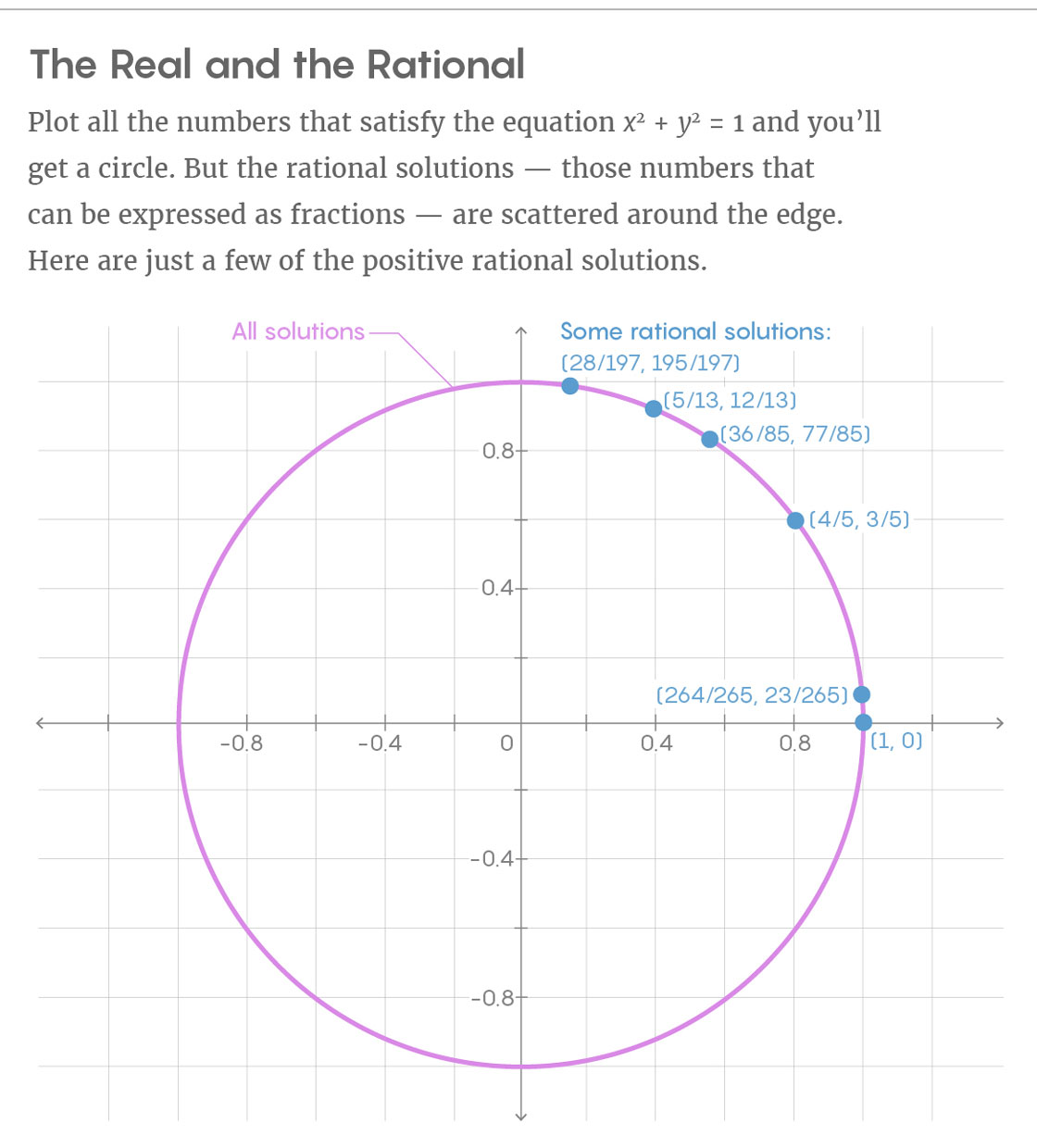
“A condição a que o ponto deve obedecer para ter coordenadas racionais não é de todo geométrica. É impossível escrever uma equação que os pontos racionais devam satisfazer ", diz Kim.
Muitas vezes, é bastante simples encontrar uma solução racional, ou mesmo várias. Mas os matemáticos que não gostam de eufemismo estão mais interessados em encontrar todas as soluções racionais. E isso é muito mais complicado. É tão difícil que a evidência de uma afirmação menor sobre o número de decisões racionais é suficiente para passar por um luminar matemático. Em 1986,
Gerd Falting ganhou o
Fields Prize , o maior prêmio em matemática, principalmente por provar
a hipótese de Mordell , segundo a qual certas classes de equações diofantinas têm apenas um número finito de soluções racionais.
A prova de Falting foi um ponto de virada na teoria dos números. E também pelo que os matemáticos chamam de "prova ineficaz", porque não forneceu o número exato de soluções racionais e não as encontrou. Desde então, os matemáticos têm procurado maneiras de executar esses próximos passos. Os pontos racionais parecem aleatórios em um gráfico de equações regular. Os matemáticos esperam que, mudando o contexto em que refletem sobre um problema, esses pontos possam parecer uma combinação significativa que possa ser descrita de alguma maneira exata. O problema é que áreas conhecidas da matemática não fornecem esse contexto.
Kim em seu escritório em Oxford"Para obter resultados efetivos a partir de pontos racionais, há claramente uma necessidade de uma nova idéia", disse Ellenberg.
Agora, existem duas premissas principais sobre a natureza de uma ideia assim. Uma é do matemático japonês
Shinichi Motizuki , que em 2012 publicou um
trabalho matemático complexo e inovador de várias centenas de páginas na página de seu corpo docente na Universidade de Kyoto. Cinco anos depois, esse trabalho permanece em grande parte incompreensível. Outra idéia nova veio de Kim, que tentou imaginar números racionais em um contexto numérico estendido no qual seus padrões ocultos começam a aparecer.
Solução simétrica
Os matemáticos costumam dizer que quanto mais simétrico um objeto, mais fácil é estudá-lo. Portanto, eles gostariam de colocar o estudo de equações diofantinas em condições que contenham mais simetria do que naquelas em que esse problema surge naturalmente. Se isso der certo, eles poderão usar as novas simetrias para rastrear os pontos racionais de que precisam.
Para entender como a simetria ajuda um matemático a resolver um problema, imagine um círculo. Talvez seu objetivo seja identificar todos os pontos do círculo. A simetria ajuda muito, porque cria um mapa que permite mover de pontos que você conhece para aqueles que ainda precisam ser descobertos.
Imagine que você encontrou todos os pontos racionais no fundo de um círculo. Como o círculo possui simetria no espelho, os pontos podem ser refletidos para cima (alterando os sinais em todas as coordenadas y) e subitamente obtendo todos os pontos do topo. O círculo em geral tem uma simetria tão rica que, para procurar todos os pontos nele, é necessário descobrir a posição de apenas um ponto e combiná-lo com o conhecimento sobre a simetria do círculo: basta aplicar a simetria rotacional infinita do círculo ao ponto inicial.
Mas se o objeto geométrico com o qual você trabalha é muito menos correto, como, por exemplo, um caminho aleatório, você precisará trabalhar muito para determinar cada ponto separadamente - não terá relacionamentos simétricos que permitam marcar pontos desconhecidos quando ajudar famoso.
Conjuntos numéricos também podem ter simetrias, e quanto mais simetrias em um conjunto, mais fácil é entender - você pode aplicar relacionamentos simétricos para detectar valores desconhecidos. Números com certos tipos de simetria formam um "grupo", e os matemáticos usam as propriedades do grupo para entender os números contidos nele.
Muitas soluções racionais da equação não precisam ter simetria e não formam um grupo, razão pela qual os matemáticos são confrontados com uma tarefa irrealista na tentativa de encontrar soluções uma de cada vez.
A partir da década de 1940, os matemáticos começaram a estudar métodos para organizar as equações diofantinas em condições mais simétricas. O matemático Claude Chabauty descobriu que dentro do espaço geométrico maior que ele criou (usando um universo extenso de números chamado números
p-adic ), os números racionais formam seu próprio subespaço simétrico. Ele pegou esse subespaço e o
combinou com um gráfico da equação diofantina. Os pontos de sua interseção acabaram sendo soluções racionais da equação.
Nos anos 80, o matemático
Robert Coleman especificou o trabalho de Chaboti. Nas duas décadas seguintes, a abordagem de Coleman-Chaboti foi a melhor ferramenta matemática que os matemáticos tiveram para encontrar soluções racionais para as equações diofantinas. Mas isso só funciona se o gráfico da equação se correlacionar com o tamanho de um espaço maior em uma determinada proporção. Quando está quebrado, fica difícil encontrar com precisão a posição dos pontos de interseção da curva da equação e os números racionais.
"Se a sua curva está em um ambiente onde há muitos pontos racionais, eles começam a se acumular e é difícil distinguir quais estão na curva", disse Kiran Kedlaya, matemático da Universidade da Califórnia, em San Diego.
E então Kim entra. Para expandir o trabalho de Chaboti, ele queria encontrar um espaço ainda maior no qual estudar equações diofantinas - um espaço em que os números racionais são mais fragmentados, o que nos permite estudar pontos de interseção com um grande número de variedades de equações diofantinas.
Espaços de espaços
Se você precisar de um espaço maior e algumas dicas de como usar a simetria para se orientar, a física o ajudará.
No caso geral, o espaço no sentido matemático é qualquer conjunto de pontos com uma estrutura geométrica ou topológica. Mil pontos espalhados por vontade ou não, não formam espaço - eles não são conectados por uma estrutura. Mas a esfera, que é uma organização conectada de pontos, já é espaço. Como um toro, ou um plano bidimensional, ou um espaço-tempo quadridimensional, onde vivemos.
Além desses, existem ainda mais espaços exóticos que podem ser imaginados como "espaços de espaços". O exemplo mais simples: digamos que você tenha um triângulo - e isso é espaço. Agora imagine o espaço de todos os triângulos possíveis. Cada ponto nele representa um certo triângulo e as coordenadas deste ponto são determinadas pelos ângulos do triângulo representado por ele.
Essa ideia é frequentemente útil em física. Dentro da estrutura da teoria geral da relatividade, o espaço e o tempo estão em constante evolução, e os físicos consideram cada configuração do espaço e do tempo como um ponto no espaço de todas as configurações do espaço-tempo. Os espaços também aparecem na área que os físicos chamam de invariância do medidor, trabalhando com campos sobrepostos no espaço físico. Esses campos descrevem como forças como eletromagnetismo e gravidade mudam quando se deslocam no espaço. Pode-se imaginar que em cada ponto do espaço a configuração desses campos é um pouco diferente - e que todas essas configurações diferentes formam pontos no "espaço de todos os campos" de maior dimensão.
Esse espaço de campos da física é uma analogia próxima à proposta de Kim para a teoria dos números. Para entender isso, imagine um raio de luz. Os físicos representam a luz se movendo através do espaço de campos de maior dimensão. Nesse espaço, a luz seguirá um caminho que segue o princípio de menor resistência e minimiza a quantidade de tempo necessária para ir do ponto A ao ponto B. Esse princípio explica por que a luz se curva ao passar de um material para outro - um caminho curvo minimiza o tempo custos.
Os espaços maiores de espaços que aparecem na física têm simetrias adicionais que não estão presentes em nenhum dos espaços que representam. Essas simetrias chamam a atenção para certos pontos, por exemplo, focando em um caminho que minimiza o tempo. As mesmas simetrias, construídas de uma maneira diferente e em um contexto diferente, podem ser enfatizadas em outros pontos - por exemplo, em pontos correspondentes a soluções racionais de equações.
Conectando Simetria com Física
Na teoria dos números, não há partículas que possam ser rastreadas, mas tem algo como espaço-tempo, e oferece uma maneira de desenhar caminhos e criar o espaço de todos os caminhos possíveis. A partir dessa correspondência básica, Kim desenvolve esquemas nos quais "o problema de encontrar a trajetória da luz e encontrar soluções racionais das equações diofantinas são duas faces do mesmo problema", como ele explicou em uma conferência de física matemática em Heidelberg na semana passada.
Soluções de equações diofantinas formam espaços - essas são curvas definidas por equações. Essas curvas podem ser unidimensionais, como um círculo, ou multidimensionais. Por exemplo, se você construir uma solução complexa da equação diofantina x
4 + y
4 = 1, obterá um toro com três orifícios. Os pontos racionais desse toro não têm uma estrutura geométrica - é por isso que é difícil encontrá-los - mas podem ser comparados com os pontos em um espaço multidimensional de espaços que possuem essa estrutura.
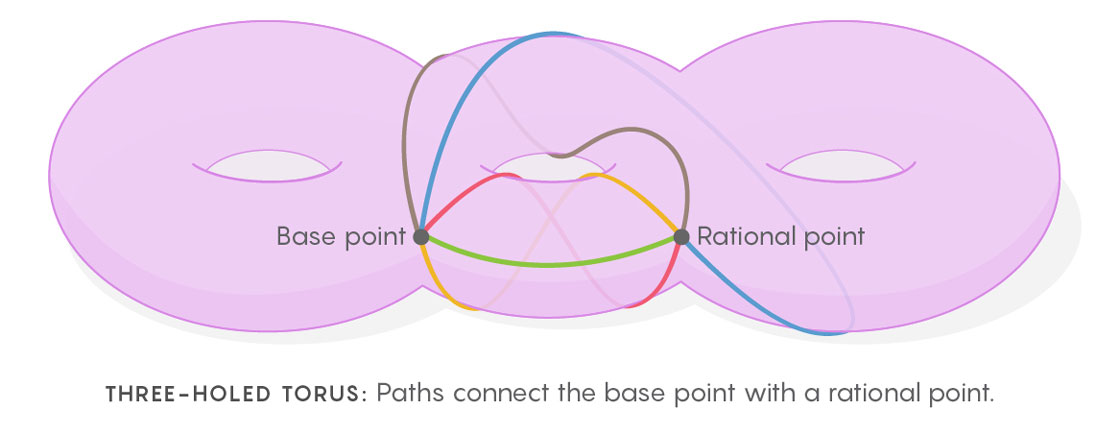
Kim cria esse espaço multidimensional de espaços, imaginando as maneiras pelas quais curvas fechadas podem ser desenhadas no toro (ou no espaço que define a equação). O procedimento para desenhar curvas é assim. Primeiro, você precisa selecionar o ponto de partida, depois desenhar um loop desse ponto para outro e retornar ao primeiro. Agora repita esse processo, desenhando os caminhos que conectam o ponto base com todos os outros pontos do toro. Você receberá o emaranhado de todos os loops possíveis começando e terminando no ponto base. Esse conjunto de loops é um objeto de importância central da matemática chamado
grupo fundamental do espaço.
Qualquer ponto no toro pode ser usado como ponto de partida. Cada ponto terá um emaranhado único de caminhos que emanam dele. Cada uma dessas coleções de caminhos pode ser representada como um ponto em um "espaço multidimensional de todos os conjuntos de caminhos" (como o espaço de todos os triângulos possíveis). Esse espaço de espaços é geometricamente muito semelhante ao que os físicos constroem na teoria da invariância do medidor: a maneira como os conjuntos de caminhos mudam quando você passa de um ponto em um toro para outro se assemelha fortemente à forma como os campos mudam quando você vai de um ponto a outro. outro no espaço real. Esse espaço de espaços possui simetrias adicionais que não estão no próprio toro. E embora pontos racionais em um toro não tenham simetria, se formos ao espaço de todos os conjuntos de caminhos, podemos encontrar simetrias entre pontos associados a números racionais. Você obtém simetrias que não eram visíveis antes.
“Às vezes digo que a“ simetria aritmética oculta ”é codificada nesses caminhos, o que é muito semelhante às simetrias internas da teoria da invariância do medidor”, disse Kim.
Como Chaboti, Kim encontra soluções racionais explorando os pontos de interseção no espaço maior que eles criaram. Ele usa as simetrias desse espaço para chegar aos pontos de interseção. Ele espera desenvolver uma equação que defina com precisão esses pontos.
No contexto físico, pode-se imaginar todas as maneiras possíveis pelas quais um raio de luz pode seguir. Este é o seu "espaço de todos os caminhos". Os físicos estão interessados em pontos nesse espaço correspondentes a caminhos que minimizam o tempo. Kim acredita que os pontos correspondentes aos emaranhados de caminhos que emanam de pontos racionais têm algo em comum com a mesma propriedade - ou seja, esses pontos minimizam algumas propriedades que ocorrem quando você considera as formas geométricas das equações diofantinas. Ele apenas ainda não descobriu qual seria essa propriedade.
"O que comecei a tentar encontrar" é o princípio de menor resistência em um contexto matemático, ele escreveu em uma carta. "Ainda não o encontrei, mas tenho certeza de que existe."
Futuro incerto
Nos últimos meses, descrevi a visão de Kim, inspirada na física, por vários matemáticos, fãs de suas contribuições à teoria dos números. Mas, ao saber desses detalhes de seu trabalho, eles se perderam.
“Como um teórico de quantidades representativas, se me mostrassem todas aquelas incríveis realizações feitas pelo Minion e perguntasse se elas foram inspiradas pela física, eu diria: Do que diabos você está falando?” - disse Ellenberg.
Até agora, Kim não mencionou a física em nenhum de seus trabalhos. Em vez disso, ele escreve sobre objetos chamados "variações Selmer" e examina a relação entre variações Selmer no espaço de todas as variações Selmer. Tais coisas são familiares aos especialistas em teoria dos números. Mas para Kim, eles sempre eram apenas outra designação de certos objetos físicos."Deveria haver uma maneira de usar idéias físicas para resolver problemas na teoria dos números, mas ainda não pensamos o suficiente em como criar essa plataforma", disse Kim. "Estamos em um estado em que nossa compreensão da física é muito bem desenvolvida e muitos especialistas em teoria dos números estão interessados nela para dar o próximo passo."O principal obstáculo ao método Kim é encontrar alguma ação para minimizar o espaço de todos os conjuntos de loops. No mundo físico, essa abordagem parece natural, mas na aritmética não tem um significado óbvio. Mesmo os matemáticos que ficam de olho no trabalho de Kim não têm certeza se ele pode encontrá-lo."Acho que o programa de Kim fará muitas coisas maravilhosas por nós. "Eu não acho que teremos tão claro quanto Mignon quer entender se os pontos racionais são soluções clássicas para a teoria aritmética dos medidores", disse Arnav Tripathy, professor de física matemática da Universidade de Harvard.Hoje, a linguagem da física quase não se cruza com a prática da teoria dos números. Kim acredita que isso quase certamente mudará. Quarenta anos atrás, física, geometria e topologia tinham pouco em comum. Então, na década de 1980, vários matemáticos e físicos, agora figuras significativas, encontraram maneiras exatas de usar a física para estudar as propriedades das formas. Após esse desenvolvimento, essa área mudou e não retornou aos métodos anteriores.“Hoje em dia é praticamente impossível se interessar por geometria e topologia sem saber nada sobre física. Tenho certeza de que isso também acontecerá com a teoria dos números ”nos próximos 15 anos, disse Kim. "Todas as conexões são extremamente naturais."