Dimensões adicionais: mundos bidimensionais

De um artigo sobre mundos unidimensionais, você sabe que o mundo funciona unidimensionalmente porque a posição nele é determinada por uma unidade de informação.

Também deve ser contínuo (ou quase contínuo do ponto de vista prático). Eu descrevi vários exemplos de dimensões: uma linha de receita, infinita e representada por uma linha infinita; linha arco-íris, final, com paredes delimitadoras, representada por um segmento; Linha de direção do vento eólico, finito-periódica, representada por um segmento no qual a extremidade esquerda coincide com a direita ou, o que é igual, com um círculo. De passagem, mencionei outro exemplo - um mundo que é interminável em uma direção e finito em outra. Em outro artigo, enfatizei que existem muitos tipos de medidas, mas as dimensões físicas do espaço têm propriedades únicas e especiais (além de muito óbvias) que as distinguem das medidas de outro tipo.


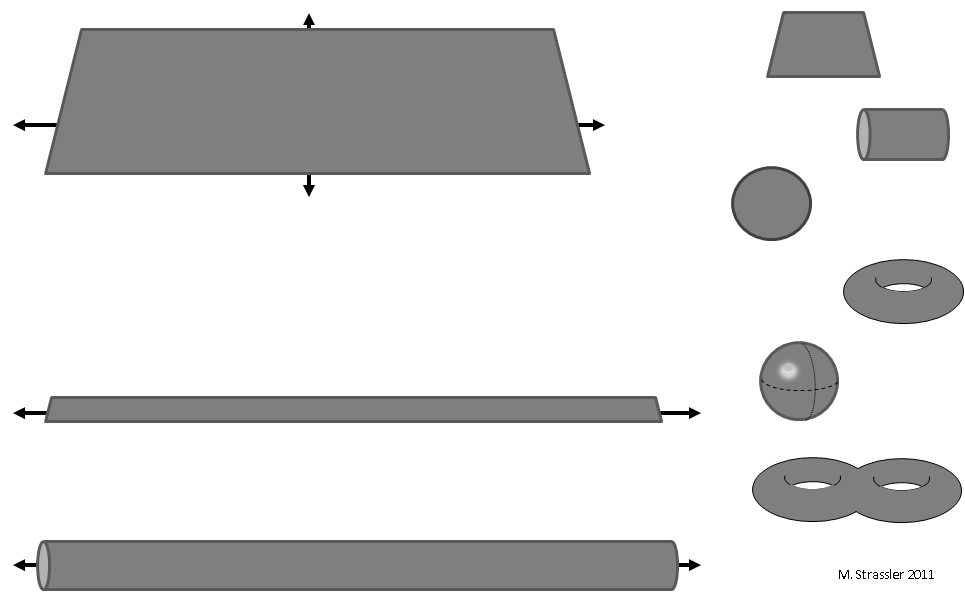Fig. 1: mundos bidimensionais

E os mundos bidimensionais? Não é de surpreender que existam muito mais tipos de mundos bidimensionais do que tipos de mundos unidimensionais. Alguns exemplos de tais espaços são mostrados na Fig. 1. Você pode imaginar um mundo sem fim nas duas direções: um avião (canto superior esquerdo). Pode-se imaginar um mundo sem fim em uma direção e em outro que forma um segmento ou um círculo. Esses mundos são naturalmente chamados de tira e tubo (canto inferior esquerdo). Pode-se imaginar o mundo final em ambas as direções (a parte direita da figura 1). E quantas oportunidades existem! Somente nesta figura você pode ver de cima para baixo um quadrado, um cilindro (a parte redonda da lata sem tampa e por dentro), um disco, um toro (algo como um pneu de carro), uma esfera (apenas a superfície), um pneu duplo. E estas não são todas as opções. Se extrapolado para o futuro, fica claro que, quando chegarmos às três dimensões e seguirmos em frente, não poderemos mais compilar essas listas.

Como nos espaços unidimensionais, a posição no espaço bidimensional é determinada por duas unidades de informação.

Um exemplo de uma esfera (com uma boa aproximação) pode ser a superfície da Terra: qualquer local pode ser indicado por latitude e longitude. Uma formiga, caminhando ao longo de uma mangueira de jardim, se move ao longo de um tubo bidimensional e a qualquer momento está localizada a uma certa distância do guindaste e a um certo ângulo em relação à vertical. Uma rodovia com várias faixas é essencialmente uma faixa bidimensional com um lado muito longo e um lado curto: as duas unidades de informações necessárias para determinar sua posição são a distância desde o início da estrada e a distância da borda direita.

Lembre-se da linha de receita. “Sua renda no ano passado é um determinado número na sua moeda local. Pode ser positivo ou negativo, grande ou pequeno; pode ser representado como um ponto em uma linha, como na fig. 1, que chamaremos de "ponto de renda". Cada ponto na linha representa um possível retorno. ” Se você é casado e você e seu cônjuge têm renda, os dois fluxos de caixa que entram em sua casa podem ser representados como um plano de duas renda. Dois números que descrevem um ponto nesse plano serão sua renda e a renda de seu cônjuge.

E aqui está um exemplo astuto de um toro mostrando como se pode imaginar formas bidimensionais interessantes cujas dimensões não são dimensões do espaço físico. Na fig. Em três artigos sobre mundos unidimensionais, vimos que as possíveis direções do vento formam um mundo unidimensional na forma de um círculo (ou uma linha na qual coincidem o início e o fim). As possíveis direções de navegação também formam um círculo semelhante. Mas todo mundo que navegou sabe que não é necessário seguir na mesma direção em que o vento sopra; se você definir a vela em ângulo, poderá se mover para oeste, mesmo que o vento sopre do norte. Portanto, se eu pedir duas informações - de qual direção o vento está soprando e em qual direção meu barco está se movendo - os dois serão pontos no círculo. Duas informações, ambas localizadas em círculo, indicam um ponto no toro.

Antes de continuar, vou mencionar uma confusão natural e generalizada. Eu já sugeri isso na descrição dos vários mundos dados acima. Não confunda as medidas das próprias formas com uma certa maneira de representar essas dimensões ou formas! A propriedade do círculo é tal que, se você for movê-lo em qualquer direção, retornará para onde começou. O círculo não tem nada por dentro ou por fora. Apenas representar um círculo na forma de uma curva fechada em um plano bidimensional parece ter uma parte interna e externa. Mas isso é simplesmente uma propriedade de representar o círculo no plano, e não uma propriedade do próprio círculo.