Eu já
dei alguns exemplos de como
dimensões adicionais podem ser representadas na natureza - dimensões no espaço, das quais nem temos consciência. Mas até agora ainda não expliquei como os cientistas podem aprender sobre sua existência.
Aqui você pode usar várias estratégias básicas, mas por enquanto vou me concentrar em uma simples consequência da existência de dimensões adicionais. Tem um caráter muito geral e leva a uma estratégia para o estudo da física de partículas, que é relevante para muitos estudos, incluindo experimentos no Large Hadron Collider.
Minha explicação será em duas etapas. No primeiro estágio, usando a física mais simples, darei a você uma compreensão intuitiva, simples, mas imperfeita (uma vez que a mecânica quântica não será levada em consideração) e fornecerei uma resposta parcialmente incorreta. Na segunda etapa, corrigirei a imprecisão, o que exigirá outra complicação adicional e você verá a resposta completa.
Porém, antes de iniciar a explicação, primeiro darei uma resposta imediatamente, para que você entenda o que preciso explicar. Aqui está - de várias maneiras, para torná-lo mais claro.
Qualquer partícula movendo-se em dimensões adicionais às já conhecidas por nós parecerá como você e eu, observadores ingênuos que não têm idéia sobre dimensões adicionais, para partículas de vários tipos, cada qual se movendo apenas em dimensões conhecidas por nós e as diferenças entre as quais muito pequeno, exceto por suas massas.
Em outras palavras: se uma partícula de um determinado tipo pode se mover em todas as dimensões, parecerá a um observador desinformado que, na natureza, não existe apenas essa partícula (movendo-se apenas nas dimensões conhecidas por ela), mas todo um conjunto de partículas relacionadas, “KK partners”. que também se move em direções conhecidas, ligeiramente diferentes da partícula original, exceto que elas serão mais pesadas. "KK" refere-se à
teoria de Kaluza-Klein , sobre a qual mais tarde.
Suponha que vivamos em quatro dimensões espaciais, três das quais são grandes (conhecidas por nós) e a quarta é muito curta (como a largura da faixa que usei nos exemplos anteriores). Em suma, significa uma distância muito curta, menor que o diâmetro do próton. Ligue para essa distância L.
Agora imagine que há uma partícula, muito, muito pequena, menor que L, que pode se mover livremente em todas as quatro dimensões espaciais. Também assumimos a existência de observadores astutos que sabem que essa partícula pode se mover em quatro dimensões e tem uma massa m. Agora consideraremos observadores ingênuos que não conhecem a pequena dimensão espacial, que acreditam que vivem em um mundo tridimensional. Após algumas experiências indicadas na fig. 1, podemos dizer: “aqui está um tipo de partícula que pode se mover em três dimensões, e tem massa m; mas veja, outro tipo de partícula, também capaz de se mover em três dimensões, e é semelhante à primeira, apenas sua massa M, muito mais que m; e, uau, aqui está outro tipo de partícula capaz de se mover em três dimensões, semelhante à primeira, só que tem uma massa M ', maior que M; e outro tipo de partícula, massa M ”; e mais e mais ... "
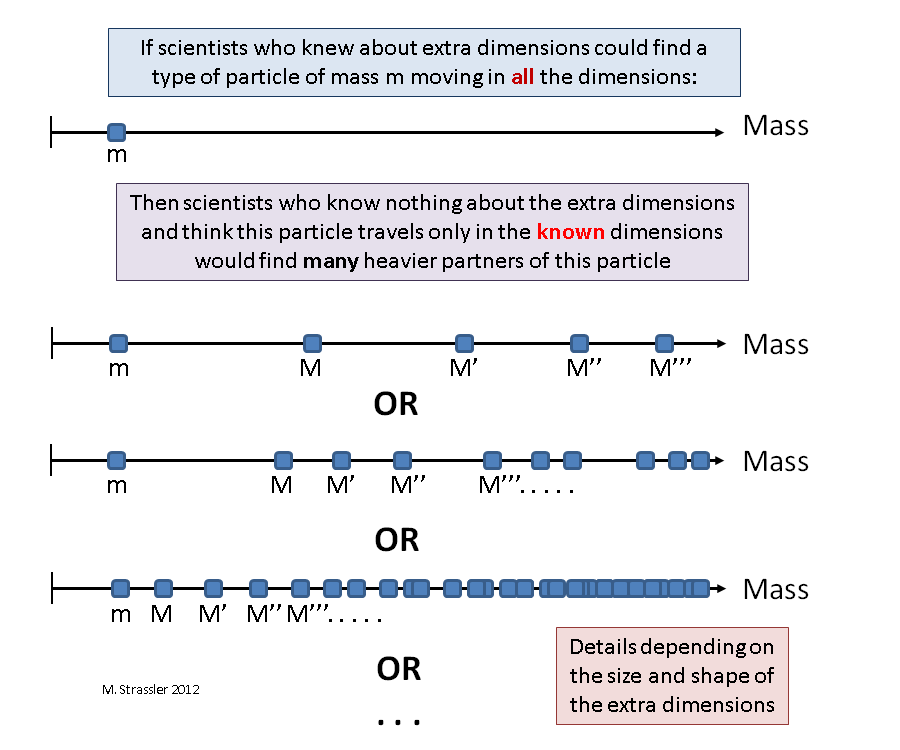Fig. 1As massas M, M ', M ”e assim por diante são determinadas pela combinação da massa fundamental me geometria das dimensões espaciais adicionais - em particular M, M', M” e assim por diante são inversamente proporcionais a L. Quanto menor L, maior M, M ', M ”e assim por diante, e mais difícil é encontrar parceiros pesados de CQ. Além disso, a sequência de massas que aparece nos parceiros de CQ fornece uma indicação direta da quantidade, tamanho e forma das medições adicionais. Você pode fazer uma analogia musical - esse fato se deve ao fato de que os harmônicos exatos produzidos pelo instrumento podem fornecer informações sobre sua forma e tamanho.
Por exemplo: se os fótons (partículas de luz) pudessem se mover em uma ou várias dimensões adicionais, como um barco em um canal, um observador que estivesse ciente de dimensões adicionais os descreveria como partículas sem massa (m = 0) se movendo em todas as dimensões . Mas um cientista humano que até agora conhece apenas um fóton sem massa se movendo em três dimensões conhecidas descobriria um conjunto de partículas pesadas semelhantes aos fótons. Quanto menor o tamanho da medição adicional, maior a massa de fótons KK e mais difícil é abri-los - mais precisamente, quanto mais pesados eles são e mais energia o acelerador de partículas precisará para gerá-los.
Pode ser que vários tipos de partículas possam se mover em dimensões adicionais e, neste caso, os cientistas descobrirão parceiros KK pesados para cada um desses tipos de partículas (veja a Fig. 2). A descoberta de um pequeno número de partículas pesadas que se assemelham a algumas das partículas de luz conhecidas, cuja distribuição de massa será semelhante à da Fig. A distribuição 2 indicará claramente que as novas partículas são parceiras do CQ e que temos uma ou mais dimensões adicionais.
Fig. 2Esta é a resposta simples: uma partícula que se move em dimensões adicionais e em dimensões conhecidas se abrirá para nós através da descoberta de seus pesados parceiros de CQ. Mais tarde, descreverei com mais precisão como você pode tentar produzir e abrir parceiros de CQ no experimento. Nos
artigos a
seguir, descreverei por que essa resposta específica será correta - e darei uma versão simples e complexa da explicação.