Parceria Parceiros Kaluza-Klein, parte 2

Em um artigo anterior, expliquei por que pareceria aos observadores ingênuos que não estão cientes da presença de uma dimensão adicional que uma partícula capaz de se mover em dimensões adicionais tenha parceiros de Kaluza-Klein (KK) - versões mais pesadas da partícula original. Afirmei que quando a partícula inicial da massa m se move na direção da dimensão adicional, parece ao observador ingênuo imóvel e mais pesado do que deveria ser, ou seja, como se fosse uma partícula de um tipo diferente. Essa classe de partículas supostamente novas, semelhante à original, mas mais pesada, é chamada de parceiro de controle de qualidade.

No caso de uma faixa , se uma partícula de massa m se mover através da faixa com um momento p, o observador que considerar a faixa como uma linha assumirá que a partícula é um parceiro KK com momento zero e massa M, onde

$$

$$M ^ 2 = m ^ 2 + (p_ {através} / c) ^ 2> m ^ 2$$

Embora isso geralmente seja verdade, segue-se que para cada massa M maior que m, deve haver seu próprio parceiro de CQ. Mas não é assim - nosso mundo é quântico (veja a Fig. 1 do artigo anterior). Agora descobrimos exatamente como a mecânica quântica muda todo o cenário.

A principal característica da física quântica de que precisamos é que, para uma “partícula” quântica se movendo em uma medida de tamanho finito, nem todos os valores possíveis de p _{transversalmente são} permitidos. Em uma formulação mais geral: a mecânica quântica sugere que uma "partícula" que se move em uma medição de tamanho finito pode ter apenas certos valores de momento nessa direção.

Essa é uma das consequências mais importantes e estranhas da mecânica quântica! À primeira vista, isso é completamente contra-intuitivo, pois o que pode impedir você de pedir à "partícula" com momento p uma ligeira aceleração, de modo que seu momento seja ligeiramente diferente de p?

O que é um quantum?

Você deve ter notado que comecei a citar a palavra “partícula”, porque no contexto atual precisamos distinguir o termo “partícula”, usado para descrever elétrons, múons, quarks, glúons e todas as outras partículas elementares conhecidas, a partir de um conceito intuitivo partículas que herdamos de nossa experiência com poeira, areia, sal e cascalho. Seria melhor chamar "partículas" como elétron, fóton, Quark etc., quanta, objetos mais astutos. Esses quanta são perturbações dos campos, são muito mais como ondas do que partículas. A melhor maneira de entender o quantum é imaginar ondas. Esse é outro ponto lingüístico importante: quando digo "onda", não quero dizer algo como uma onda separada no oceano quebrando na praia - quero dizer uma sequência de ondas com muitas cristas e vales.

Um exemplo dessas ondas serão as ondas eletromagnéticas, que também incluem ondas de luz, distinguíveis aos nossos olhos. Imagine que pegamos uma onda - por exemplo, luz laser - e diminuímos a luz cada vez mais. Como pode ser abafado? Acontece que, em nosso mundo quântico, há o menor flash de luz possível que chamamos de quantum de luz, ou fóton. Um fóton é uma onda de luz cuja altura e intensidade da onda é a menor possível. Devemos todos esses conceitos e nomes a Einstein, que - apesar de toda sua conhecida insatisfação com as conseqüências conceituais da mecânica quântica - foi um dos fundadores dessa teoria.

Não há nada intuitivo - do meu ponto de vista - que as ondas de luz são compostas de quanta, pois isso não se manifesta em nenhum dos processos que observamos diretamente. Mas nossos corpos, graças a processos dos quais não temos conhecimento, usam esse fato constantemente. A luz da lâmpada parece contínua para o nosso cérebro, mas nossos olhos realmente absorvem os fótons, um de cada vez. Além disso, vi com meus próprios olhos a confirmação de que a luz consiste em quanta - sei disso não apenas nos livros.

Nós físicos frequentemente chamamos esses quanta de luz de "partículas de luz", porque de muitas maneiras eles se comportam como partículas. Qualquer fóton que se mova em linha reta por si só tem certa energia e momento; todos os fótons têm o mesmo valor de massa (especificamente zero); um fóton não pode ser dividido em partes menores; um fóton só pode ser emitido ou absorvido na sua totalidade. Essas propriedades correspondem aproximadamente ao que nossa intuição poderia esperar de partículas como grãos de areia, bolas de vidro, partículas de poeira etc.

Mas a palavra "quantum", por muitas razões, é melhor que a palavra "partícula", uma vez que algumas propriedades dos quanta são semelhantes às propriedades das partículas e outras às propriedades das ondas. Um exemplo bem conhecido de comportamento das ondas é uma maneira quântica de passar por duas portas ao mesmo tempo e interagir (no mesmo sentido em que as ondas interagem umas com as outras e cristas com vales se destroem mutuamente) consigo mesmas. E então veremos outro exemplo.

Deve-se lembrar que o que é feito para o fóton também é feito para todas as "partículas" conhecidas. De fato, cada um deles é um tipo de quantum - as ondas da menor altura possível no campo correspondente. Um elétron é um quantum de um campo eletrônico. Quark é um quantum de um campo de quark. Partícula Z é o quantum do campo Z e assim por diante.

Quantums - QC partners

É hora de descobrir o que prometi explicar para você: por que a natureza ondulatória dos quanta implica que as massas de partículas dos parceiros KK assumam valores definidos, e nem todos os valores possíveis, grandes massas m da "partícula" original. O famoso físico Louis de Broglie , seguindo os traços das primeiras idéias de Einstein, definiu claramente pela primeira vez que a relação entre ondas, partículas e quanta implica que, para um quantum, existe uma relação entre:
• Seu impulso (uma propriedade semelhante às propriedades das partículas),
• E seu comprimento de onda (uma propriedade semelhante às propriedades das ondas) [e novamente, aqui, por "onda", queremos dizer uma sequência de ondas, e o comprimento de onda refere-se à distância entre as cristas das ondas na sequência].

E essa dependência é expressa simplesmente: momento = h / comprimento de onda

h é a famosa constante de Planck , a mesma constante fundamental da natureza que a velocidade da luz. Planck introduziu essa constante em 1900, tentando desvendar um fenômeno físico misterioso. Este foi o primeiro passo em direção à natureza quântica do mundo. Cada vez que você tenta descrever um fenômeno no qual a mecânica quântica desempenha um papel importante, a constante h aparece. Em muitas fórmulas, você pode ver o valor ℏ, e este é apenas h dividido por 2π, pois esse valor geralmente é mais conveniente para simplificar as fórmulas.


Fig. 1: considere um quantum se movendo ao longo de uma faixa e ao longo de um tubo

Em alguns casos, é um pouco mais fácil explicar o que acontece com o quantum que se move ao longo do tubo do que com o que se move ao longo da faixa que usamos nos exemplos anteriores. Quase tudo o que funciona para o tubo será verdadeiro para a tira. Portanto, eu vou usá-los juntos.

O parceiro QC mais leve

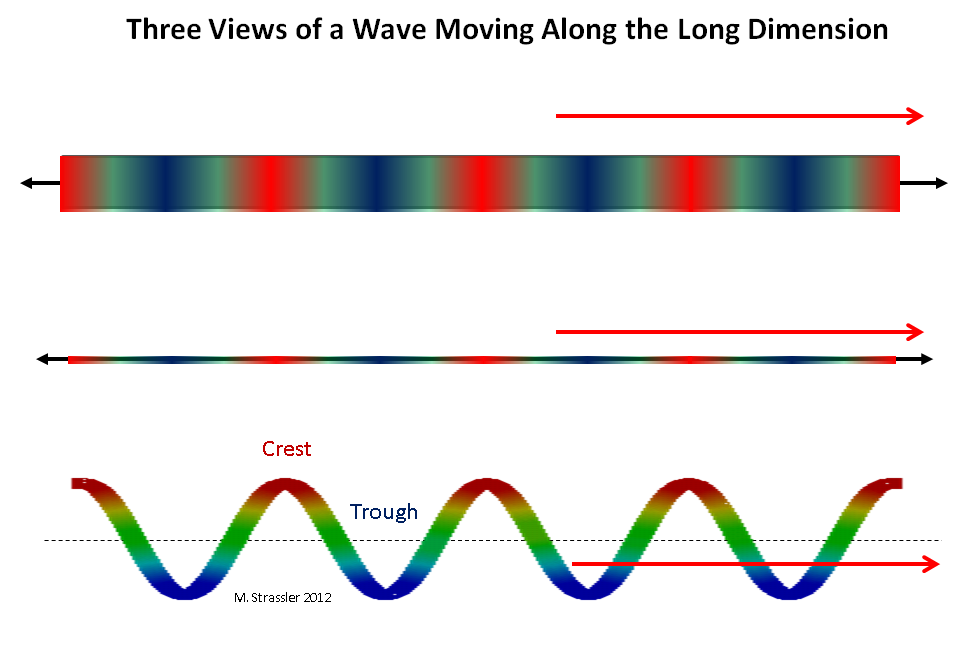Fig. 2: três vistas de uma onda se movendo ao longo de uma longa dimensão

Imagine um quantum viajando ao longo de uma faixa de largura W, ou ao longo de um tubo do círculo S. Primeiro, imagine um quantum se movendo ao longo de uma dimensão longa (long significa infinito, ou tanto tempo que pode ser infinito, tanto quanto podemos julgar). Uma onda que corre ao longo de uma tira ou tubo pode se mover ao longo de uma dimensão longa em qualquer direção e ter qualquer comprimento de onda (a distância entre duas cristas adjacentes). Veja a fig. 2. Esse quantum pode ter qualquer momento ao longo de uma tira ou tubo, de acordo com Broglie: o momento pode ser zero, muito pequeno, pequeno, grande, em qualquer direção, etc. Em princípio, um impulso pode ser feito um pouco mais (ou um pouco menos) empurrando um quantum na direção de seu movimento (ou no oposto).


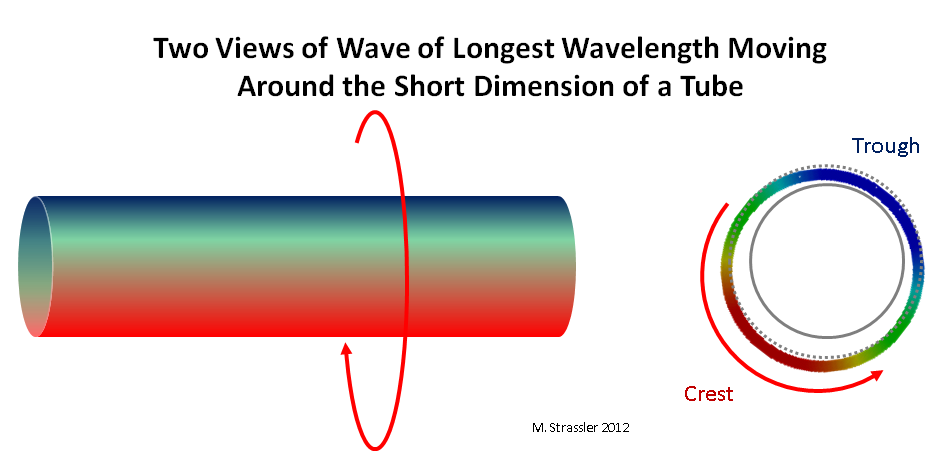Fig. 3: duas vistas de uma onda se movendo ao longo de uma dimensão curta de um tubo

Agora considere um quantum (isto é, “partícula”) se movendo através de uma tira ou tubo. Em primeiro lugar, obviamente não será possível ter um comprimento de onda maior que a distância transversal da faixa ou a circunferência do tubo! Isso é fácil de ver no tubo: pelo menos uma crista (vermelha) e uma depressão (azul) que se encaixam ao longo do tubo, conforme mostrado na fig. 3. Se o comprimento de onda for maior que S, a onda não será conectada a si mesma, como mostrado na Fig. 4. O comprimento de onda mais longo será exatamente S; e a única cavidade da onda deve estar localizada exatamente no lado do tubo oposto à única crista.


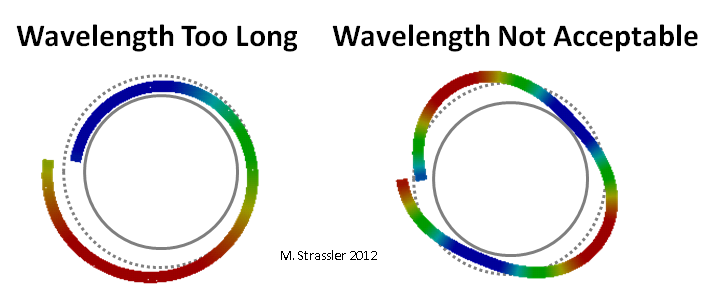Fig. 4: comprimentos de onda impróprios

A crista e a calha da onda na Fig. 3 se movem ao redor do tubo, parecendo (Fig. 5) uma partícula não quântica comum (aqui eu realmente quero dizer algo como um grão de areia, não um quantum ou uma “partícula”) rolando ao longo do tubo, mas com uma diferença importante: se uma partícula intuitiva comum não tiver problemas pode se mover um pouco mais rápido ou mais devagar, por causa do qual seu momento aumentará ou diminuirá ligeiramente, o quantum correspondente à onda não pode ter um momento um pouco maior ou menor, pois isso corresponderia a um comprimento de onda inaceitável (Fig. 4).


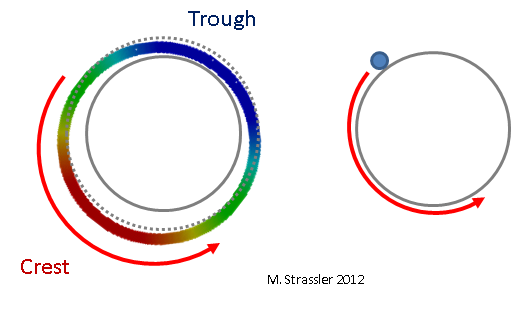Fig. 5: onda semelhante a partículas

Em uma tira é um pouco mais complicado, mas como mostrado na fig. 6, novamente, só pode haver uma crista em uma parede e uma na outra, e essa situação muda com o tempo: a crista não se move, mas diminui de tamanho e se transforma em uma cavidade, e a cavidade se transforma em uma crista. Observe que, ao contrário da Fig. 3, onde a crista e a vala mantêm seu tamanho, mas se movem ao longo do tubo, a crista dessa onda não se move, mas se contrai. Portanto, é chamada de "onda estacionária". Para um exemplo semelhante (mas não idêntico), imagine uma corda de um violão ou violino. Intuitivamente, essa onda estacionária corresponde a uma partícula não-quântica comum que se move para frente e para trás através de uma faixa. (Menos intuitivamente, mas mais precisamente, corresponde a uma partícula comum que se move em ambas as direções ao mesmo tempo. Mas esse fato quântico muito estranho e frio agora não é importante.) Isso é mostrado na Fig. 7)


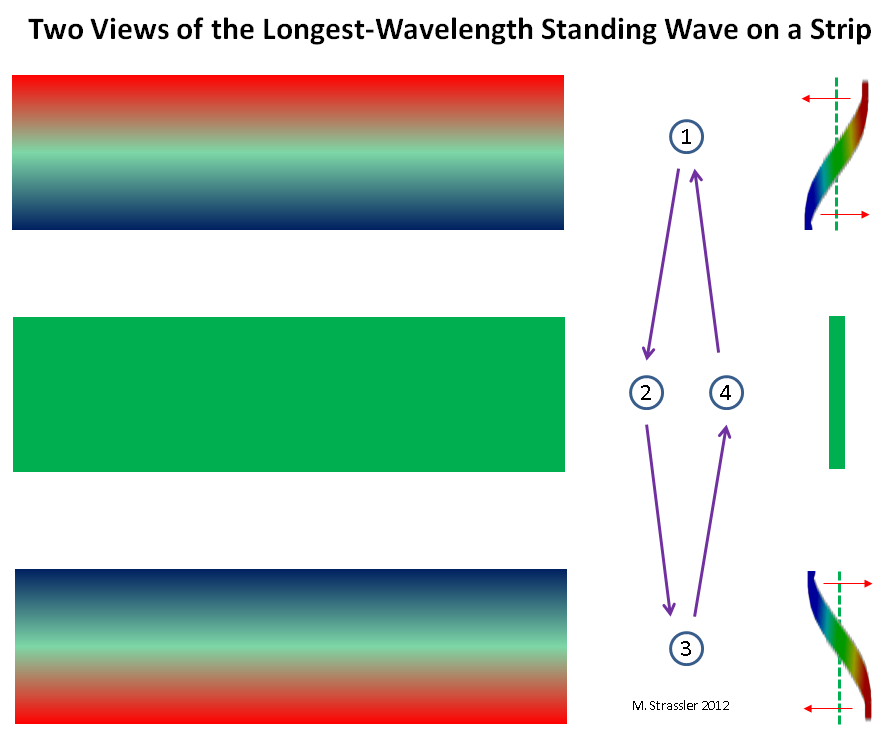Fig. 6: duas vistas da onda estacionária com o maior comprimento de onda

Nos dois casos, há o maior comprimento de onda possível (S para tubo, 2W para tira). E isso significa que existe o menor impulso possível (h / S eh / 2 W para o tubo e a tira). E, finalmente, isso significa que existe a partícula KK mais fácil possível! Com a massa M, onde

$$

$$M ^ 2 = m ^ 2 + (p_ {transversalmente} / c) ^ 2 = m ^ 2 + (h / c S) ^ 2 \ quad (pipe) \\ M ^ 2 = m ^ 2 + (p_ { entre} / c) ^ 2 = m ^ 2 + (h / 2 c W) ^ 2 \ quad (strip)$$

Observe que, para partículas sem massa, m = 0, essas fórmulas são reduzidas para:

$$

$$M = h / c S \ quad (tubo) \\ M = h / 2 c W \ quad (strip)$$

E essas últimas fórmulas estão aproximadamente corretas se S e W forem muito pequenas, como costuma acontecer no raciocínio plausível.


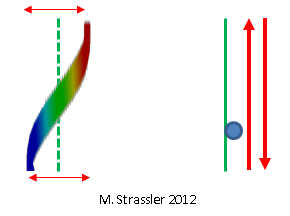Fig. 7: o quantum de uma onda estacionária é um pouco como uma partícula que se move para frente e para trás

E assim aprendemos que, devido ao fato de as "partículas" serem realmente quanta, com propriedades semelhantes às propriedades das ondas:

• No parceiro KK mais leve, a massa M é bem maior que m,
• Como as fórmulas para M incluem 1 / W e 1 / S, quanto menor a dimensão adicional, mais difícil o parceiro KK mais leve.
• De fato, quando S e W se tornam tão pequenos que M excede muito m (ou se m é inicialmente zero), então M é aproximadamente proporcional a 1 / S ou 1 / W.

Ótimo. Esse é o ponto principal, portanto, certifique-se de entendê-lo antes de continuar. Mais uma coisa a ser explicada:

• Por que existem muitos parceiros KK com diferentes massas M, M ', M ”etc. (onde, por definição, M <M '<M "etc.)
• Por que essas massas são separadas umas das outras.
• Por que as massas crescem com a redução da dimensão extra.
• Por que os parceiros KK de diferentes tipos de partículas capazes de se mover na mesma dimensão adicional têm massas semelhantes, especialmente para parceiros KK mais pesados.
• Por que as massas de parceiros de CQ nos fornecerão informações diretas sobre a forma, tamanho e número de medições adicionais.

As respostas acima podem ser facilmente deduzidas.

Além do parceiro mais leve de controle de qualidade

Fig. 8: onda mais próxima do comprimento de onda mais longo, movendo-se ao longo da dimensão curta do tubo

Por que existem muitos parceiros KK? Só porque as ondas quânticas em uma tira ou tubo podem ter muitos comprimentos de onda diferentes. Na fig. 8, 9 e 10, pode-se ver ondas com comprimento de 1/2 ou 1/3 do máximo, correspondendo (segundo Einstein e de Broglie) a um quantum de impulsos duplos e triplos em relação ao mínimo.


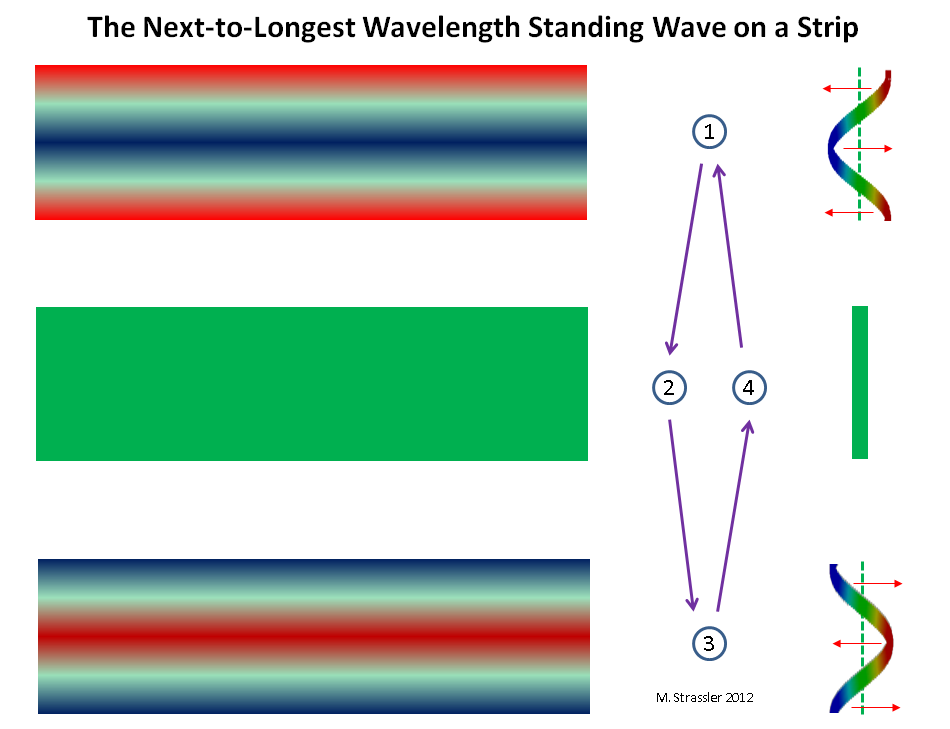Fig. 9 onda estacionária mais próxima do comprimento de onda mais longo da faixa

Resumindo, podemos dizer que é permitido qualquer comprimento de onda que tenha n cumes e vales, onde n é qualquer número inteiro positivo (1, 2, 3, 4, ..), de modo que o comprimento de onda seja igual a S dividido por n (ou 2W dividido por n) e a onda se encaixa claramente dentro de um círculo S ou dentro de uma linha de comprimento W. Qualquer outro comprimento de onda não é adequado (veja a Fig. 4). Assim, considerando a relação de Broglie, momentum = h / wave_length, qualquer impulso da forma nh / S (ou nh / 2 W) é permitido e, para cada valor de n, teremos um parceiro de massa KK:

$$

$$M ^ 2 = m ^ 2 + (p_ {através} / c) ^ 2 = m ^ 2 + (nh / c S) ^ 2 \ quad (pipe) \\ M ^ 2 = m ^ 2 + (p_ { entre} / c) ^ 2 = m ^ 2 + (nh / 2 c W) ^ 2 \ quad (strip)$$

Isso responde a quase todas as perguntas feitas, pelo menos nos casos com cano e tira:

• Existem muitos parceiros de CQ (um para cada n> 0),
• Suas massas estão bem separadas uma da outra (já que quando n muda por 1, M muda muito),
• Suas massas crescem com uma diminuição em dimensões adicionais (já que os últimos termos nas fórmulas se tornam maiores quando W e S se tornam menores),
• Parceiros KK pesados ​​de partículas diferentes com massas diferentes m têm massas semelhantes M, porque para n suficientemente grandes os segundos termos nas fórmulas são grandes em comparação com m ² , o que dá à massa do parceiro KK aproximadamente igual a M = nh / c S para o tubo e nh / 2 c W para a tira, e é quase independente de m.

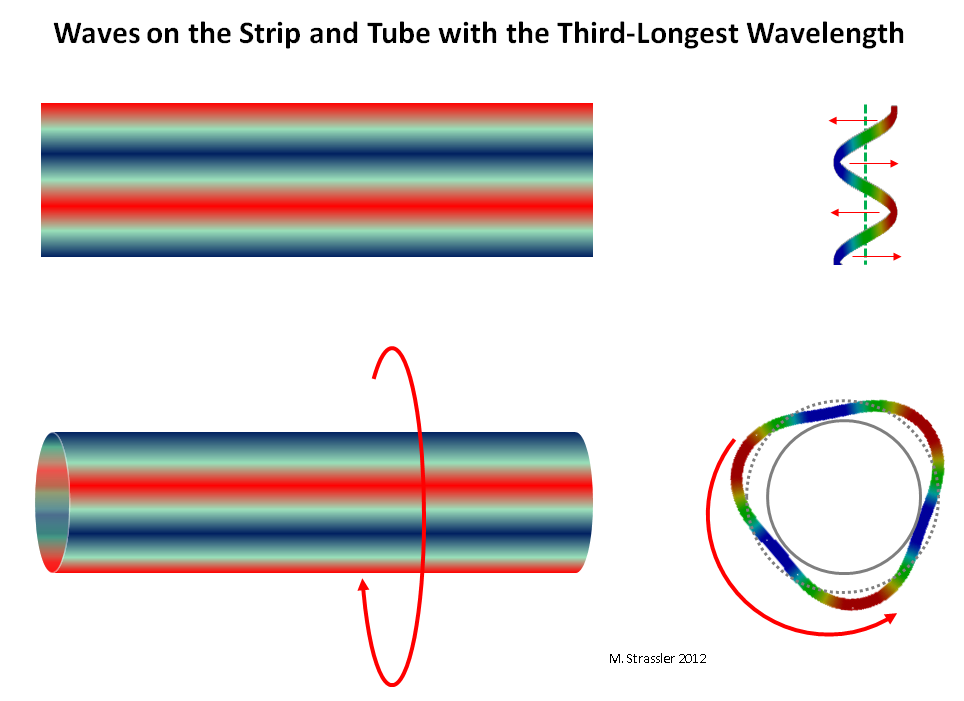Fig. 10: ondas em uma tira e um tubo com comprimento de onda de 1/3 no máximo

A última pergunta permanece: por que a quantidade, o tamanho e o formato das dimensões adicionais determinam as massas dos parceiros KK - e, portanto, por que a medição de massa de muitos parceiros KK permite determinar as propriedades de medições adicionais, assim como ouvir o som de um instrumento musical, determina basicamente sua forma , tamanho e materiais de que é feito?

Veja um exemplo extremamente simplificado. Consideraremos duas dimensões adicionais, novamente usando nosso canal de navio clássico, incluindo (como fizemos no final de um artigo recente com exemplos de medições adicionais) e o fato de o canal ter profundidade, para que possamos imaginar as ondas dentro dele (ondas deste tipo, você pode ouvir em uma sala grande ou embaixo d'água em qualquer canal). A seção do canal (se a cortarmos em qualquer ponto da linha ao longo da dimensão longa) será apenas um retângulo de largura W e profundidade D. Assim como qualquer partícula não quântica, mesmo estacionária do ponto de vista da dimensão longa, ela pode se mover ao longo de uma ou duas medições (e, portanto, têm um pulso em largura ou em profundidade) e a onda terá um comprimento de onda em ambas as dimensões adicionais. Uma divisão tão simples da onda no que faz medindo a largura e o que faz medindo a profundidade está especialmente ligada à retangularidade do canal, e geralmente não funcionará em outros exemplos. Por exemplo, como mostrado na fig. 11, no topo, uma das ondas permitidas terá três calhas para medir a largura e uma para medir a profundidade.


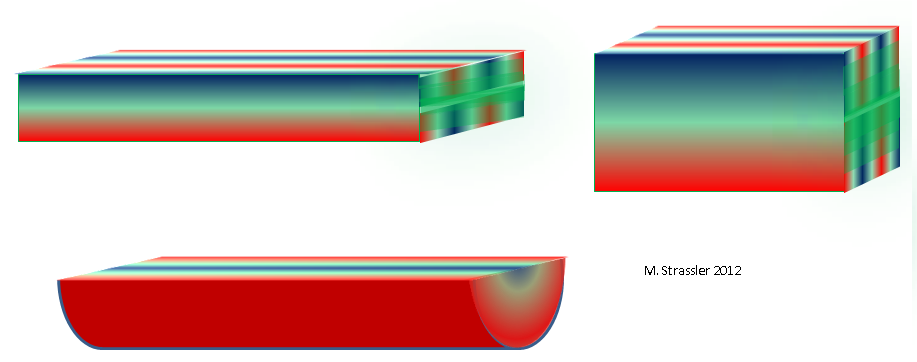Fig. 11

Podemos designar o número de depressões e cristas medindo a largura com o número inteiro n ₁ e medindo a profundidade - n ₂ , e para cada n ₁ e n ₂ (um ou ambos esses valores podem ser maiores que zero), obtemos o parceiro KK. Para quanta sem massa (m = 0) ou quase sem massa, os parceiros KK terão massa

$$

$$M ^ 2 = m ^ 2 + (p_ {width} / c) ^ 2 + (p_ {depth} / c) ^ 2 = m ^ 2 + (n_1 h / 2 c W) ^ 2 + (n_2 h / 2 c D) ^ 2$$

Pode-se ver que a distribuição de massa é diferente do caso com uma dimensão adicional e pode nos dizer tanto W quanto D.

Se a seção transversal do canal tiver uma forma diferente, por exemplo, um triangular ou meio disco, como mostrado na Fig. 11, abaixo, temos outra distribuição de massa que reflete a forma exata de um triângulo ou meio disco. E já podemos descartar os canais práticos da nave e representar o espaço tridimensional, cuja seção transversal corresponde a qualquer outra forma bidimensional finita, uma das quais é mostrada na Fig. 1 em um artigo sobre mundos com duas dimensões espaciais: um disco cheio, ou mesmo uma esfera ou toro. Cada uma dessas formas nos dará seu próprio tipo de distribuição em massa de parceiros de CQ. E se haverá três, ou quatro ou cinco dimensões adicionais ... Talvez muito mais tipos de distribuições.

Exemplos de algumas distribuições para partículas sem massa com tamanhos de medições adicionais escolhidas para que as massas dos primeiros parceiros KK sejam os mesmos para cada caso são dadas na Fig. 12. É óbvio que, para estabelecer a forma e o tamanho de medições adicionais, é necessário medir as massas de um número suficientemente grande de parceiros KK (e pelo menos confirmar que qualquer uma das partículas pesadas recentemente descobertas são geralmente parceiros KK), portanto, para entender a natureza de qualquer medições, o tempo vai passar.


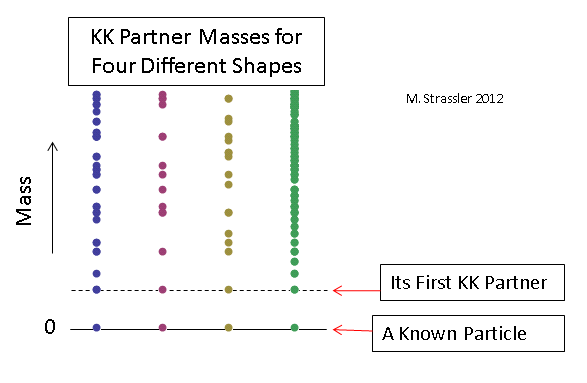Fig. 12

Mas as partículas pesadas conhecidas da matéria podem ser parceiras KK das mais leves?

Então surge a pergunta adicional óbvia.Sabemos que entre as partículas elementares conhecidas existe um elétron, bem como suas versões mais pesadas: múon e tau. Há um quark superior e suas versões mais pesadas são encantadas e verdadeiras. Há um quark mais baixo, e suas versões mais pesadas, estranhas e encantadoras. As versões de partículas pesadas são parceiras do controle de qualidade dos pulmões?

À primeira vista, essa é uma suposição tentadora, mas a resposta a ela será um firme não. Desculpe.Esta não é uma pergunta idiota. Apenas tem uma resposta negativa inteligente.

Muon e tau, encantados e verdadeiros, estranhos e encantadores - todos ganham massa graças ao campo de Higgs, e não graças ao impulso de dimensões adicionais. Isso resulta claramente de experiências detalhadas. Dicas podem ser encontradas no artigo sobre o que aconteceria se o campo Higgs fosse zero . Observe que, se o campo de Higgs fosse zero em média, o elétron, o múon e o tau não teriam massa (e cada um seria dividido em dois tipos de partículas). Isso não corresponde à teoria de que o múon e a tau são parceiros KK do elétron.

Existem muitas outras razões. O mais sério deles, talvez, seja que, devido à presença de uma carga no elétron e pelo fato de estar cercado por um campo elétrico, o fóton deva se mover em qualquer dimensão em que o elétron se mova (embora o inverso não seja verdadeiro). Portanto, se o elétron tem parceiros KK, então o fóton deve tê-los também. Mas segue-se de nossas fórmulas (e similares mais generalizadas) que, uma vez que o fóton não tem massa, e a massa de elétrons (0,0005 GeV / c ² ) é pequena em comparação com a massa do múon (cerca de 0,1 GeV / c ²), se o múon for um parceiro KK, o fóton deverá ter um parceiro KK de massa semelhante. Mas tal partícula, se existisse, teria sido descoberta há muitos anos. De fato, parceiros KK de fótons não foram observados em experimentos em que massas foram estudadas muito maiores que a massa de partículas Z - são centenas de GeV / s ² . A partícula Z em si também não pode ser um parceiro de CQ de um fóton; ela não se parece com ele o suficiente. E isso significa que quaisquer parceiros KK do elétron devem ser pelo menos tão pesados.

Para onde ir a seguir? Para experimentos

Passamos da teoria (a possibilidade de medições adicionais, matemática e geometria relacionadas) às previsões (parceiros de CQ). Próxima etapa: o que sabemos sobre medições adicionais de experimentos? Ainda não vimos parceiros da KK nos experimentos, mas podemos perguntar: o que podemos aprender com a ausência deles? Muito, como explicarei mais adiante, juntamente com uma descrição de como as tentativas de encontrar sinais de medidas adicionais continuam no Large Hadron Collider e em outros lugares.